Đề cương ôn tập giữa kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản
20 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Đồ thị được cho trong hình vẽ dưới đây là của hàm số nào?
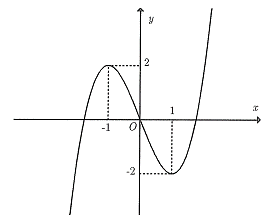
\[y = {\rm{ }}{x^4} - 2{x^2}\].
\[y = {x^{\rm{3}}} - 3x - 1\].
\[y = - {x^{\rm{3}}} + 3x\].
\[y = {x^3} - 3x\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
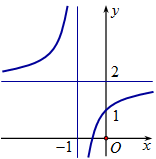
\(y = \frac{{2x - 1}}{{x + 1}}\).
\(y = \frac{{2x + 1}}{{x + 1}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{2x + 1}}{{x - 1}}\).
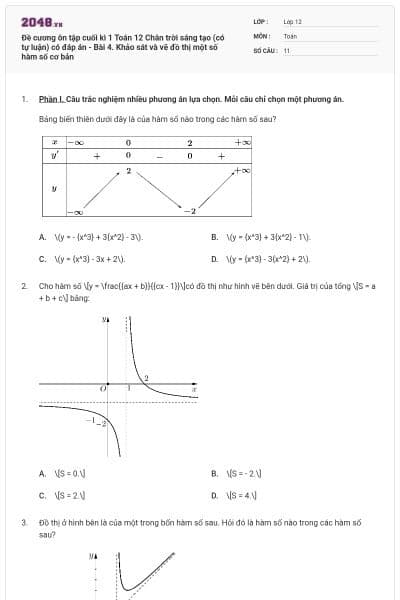
Bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó.

\(y = \frac{{2x - 3}}{{x + 1}}\).
\(y = \frac{{2x + 3}}{{x + 1}}\).
\(y = \frac{{ - 2x - 3}}{{x + 1}}\).
\(y = \frac{{ - x + 1}}{{x - 2}}\).
Đồ thị hàm số \(y = {x^3} - 3x + 2\) là hình nào trong 4 hình dưới đây?
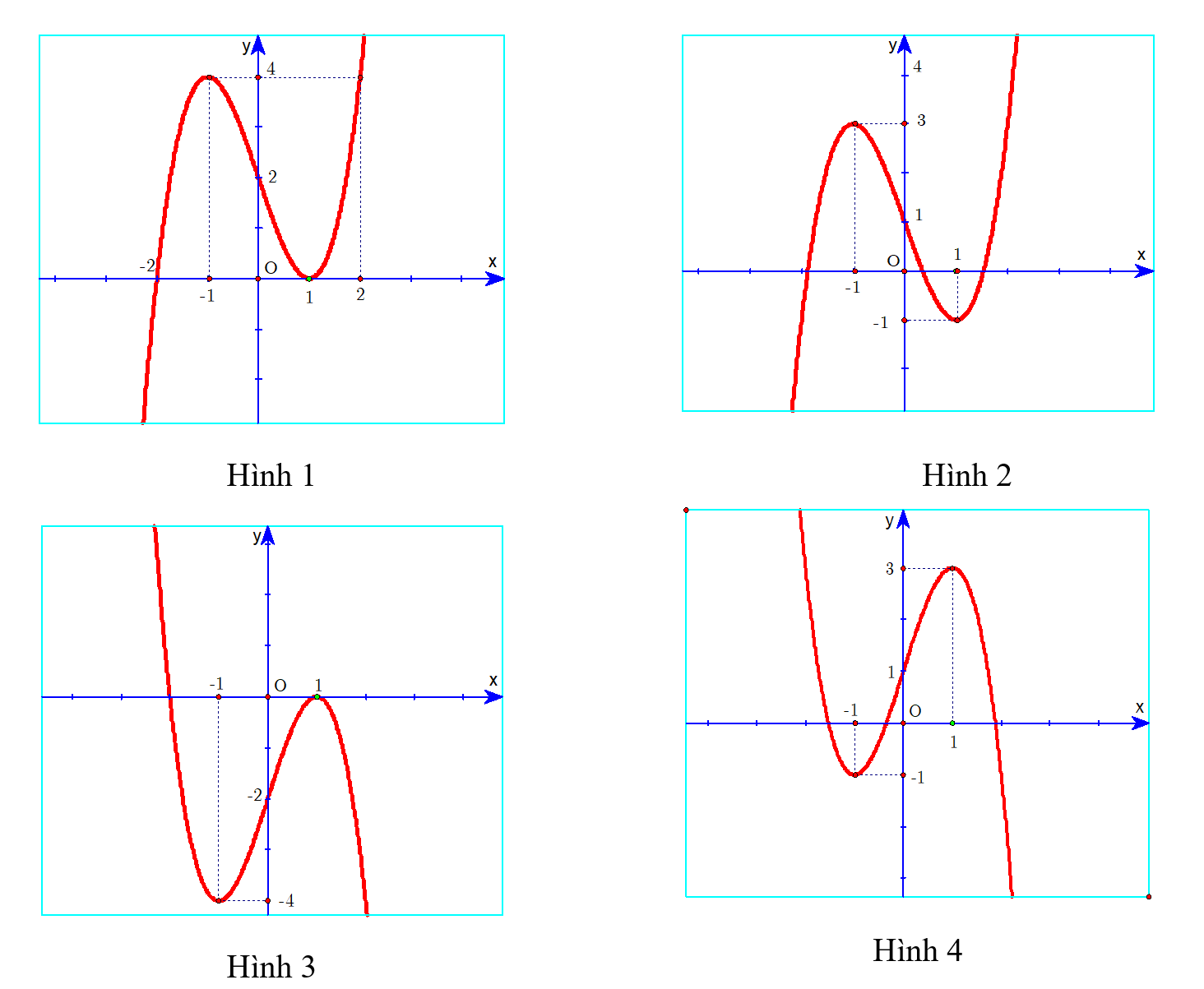
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\] có đồ thị như hình vẽ bên dưới.
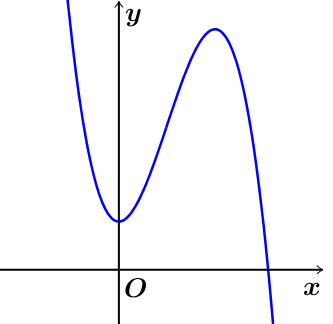
Mệnh đề nào dưới đây đúng?
\[a < 0,b > 0,c > 0,d > 0\].
\[a < 0,b < 0,c = 0,d > 0\].
\[a > 0,b < 0,c > 0,d > 0\].
\[a < 0,b > 0,c = 0,d > 0\].
Cho hàm số \(y = \frac{{x + b}}{{cx + d}}\) có đồ thị như hình vẽ bên
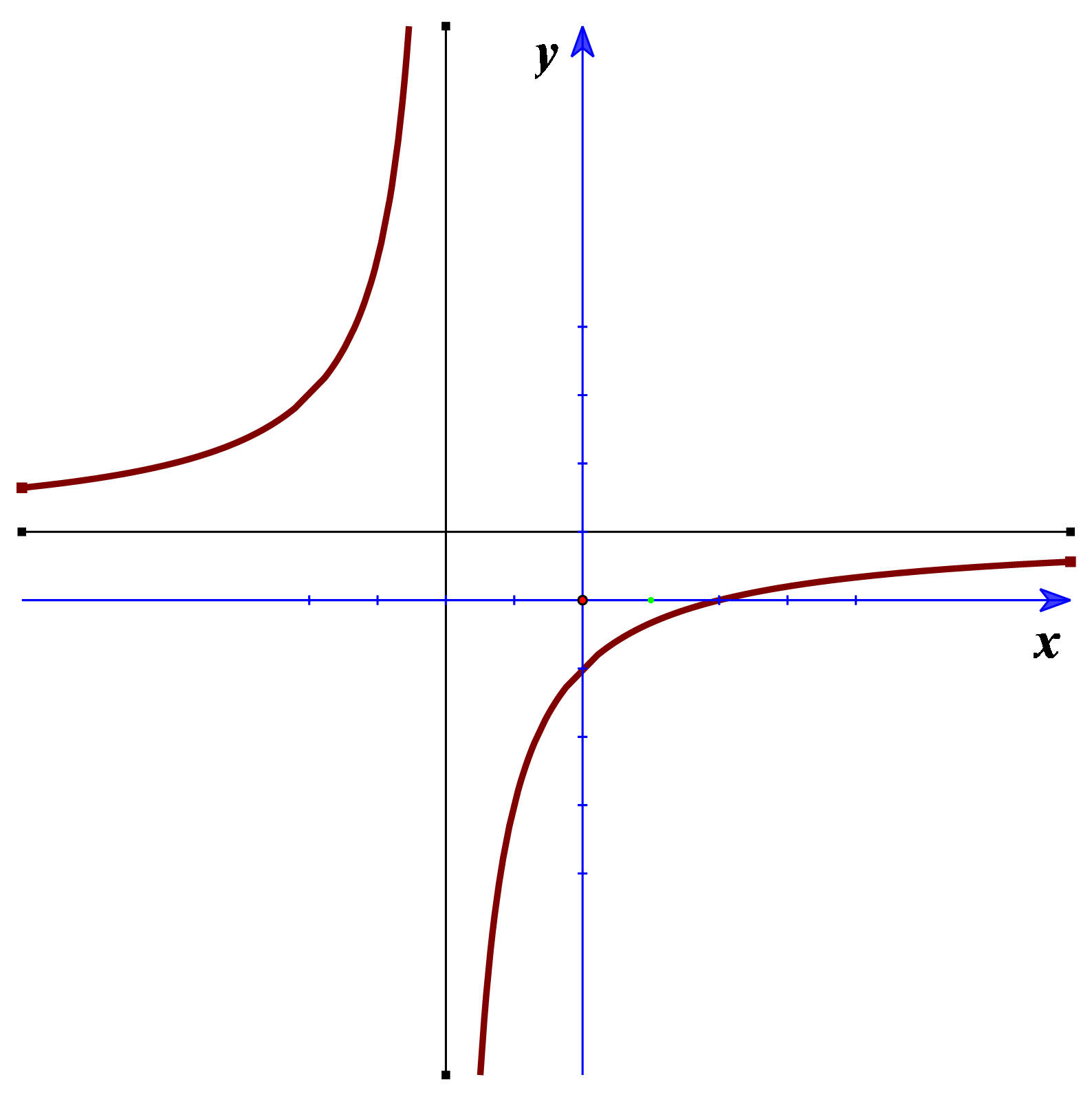
Xác định dấu của các hệ số \(b\), \(c\), \(d\).
\(b < 0,\,c > 0,\,d > 0\).
\(b < 0,\,c > 0,\,d < 0\).
\(b > 0,\,c < 0,\,d > 0\).
\(b > 0,\,c < 0,\,d < 0\).
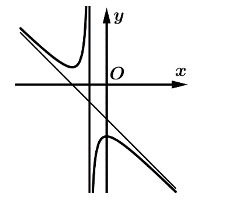
Đường cong trong hình là đồ thị của hàm số nào dưới đây?
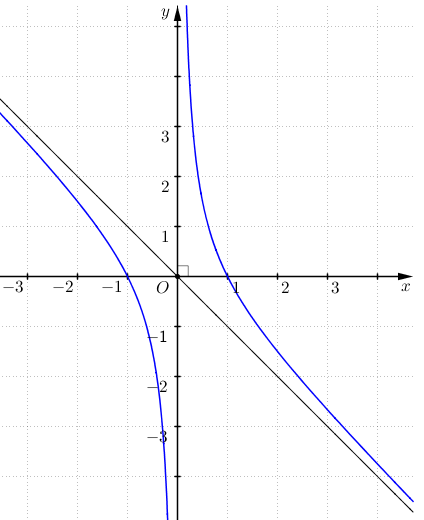
\(y = \frac{{ - {x^2} + 1}}{x}\).
\(y = \frac{{ - 2x + 1}}{{2x + 2}}\).
\(y = \frac{{{x^2} - x + 1}}{{x - 1}}\).
\(y = {x^3} - 3{x^2}\).
Bảng biến thiên sau là của một trong bốn hàm số sau.
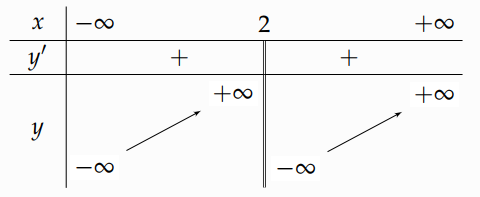
Hỏi đó là hàm số nào?
\(y = \frac{{{x^2} - 3}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\).
\(y = \frac{{{x^2} - x}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\).
Một chất điểm chuyển động có phương trình \(S = {t^3} - 3{t^2} - 9t + 2\), trong đó t được tính bằng giây và S được tính bằng mét. Gia tốc tại thời điểm vận tốc bị triệt tiêu là:
\[ - 9{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[9{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[ - 12{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[12{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng \(10{\rm{ }}{{\rm{m}}^{\rm{3}}}\). Thùng tôn là hình hộp chữ nhật có chiều dài đáy bằng hai lần chiều rộng và không có nắp. Trên thị trường giá tôn làm đáy thùng là \(75000/{{\rm{m}}^{\rm{2}}}\) và giá tôn làm thành xung quanh thùng là \(55000/{{\rm{m}}^{\rm{2}}}\). Tính chi phí thấp nhất để làm thùng đựng gạo. (Làm tròn đến hàng đơn vị)
\(1418000\) đồng.
\(1403000\) đồng.
\(1402000\) đồng.
\(1417000\) đồng.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - {x^2} + x + 1}}{{x + 1}}\) có đồ thị (C).
a) Hàm số đồng biến trên khoảng \(( - 2, - 1)\)và \(( - 1,0)\).
b) Hàm số có hai điểm cực trị.
c) Đồ thị \((C)\) không cắt trục \(Ox\).
d) Đồ thị \((C)\) có tiệm cận xiên đi qua điểm \(A(1;2)\)
Cho hàm số \(y = \frac{{m{x^2} + (3{m^2} - 2)x - 2}}{{x + 3m}}\) (1), với \(m\) là số thực.
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số có đường tiệm cận xiên là \(y = x - 2\).
c) Khi \(m = 1\) giao điểm của đường tiệm cận xiên và tiệm cận đứng của đồ thị hàm số là \(I\left( {3; - 5} \right)\).
d) Có 2 giá trị \(m\) để góc giữa hai tiệm cận của đồ thị hàm số (1) bằng \(45^\circ \).
Cho hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
a) Hàm số đã cho đồng biến trên các khoảng \(( - \infty ; - 2)\) và \((0; + \infty )\).
b) Hàm số đã cho không có cực trị.
c) Đồ thị hàm số có đường tiệm cận xiên là \(y = x\).
d) Đồ thị hàm số có tâm đối xứng là \(I( - 1; - 1)\).
Xét một chất điểm chuyển động dọc theo trục \(Ox\). Toạ độ của chất điểm tại thời điểm \(t\) được xác định bởi hàm số \(x(t) = {t^3} - 6{t^2} + 9t\) với \(t \ge 0\). Khi đó \(x'(t)\) là vận tốc của chất điểm tại thời điểm \(t\), kí hiệu \(v(t);v'(t)\) là gia tốc chuyển động của chất điểm tại thời điểm \(t\), kí hiệu \(a(t)\).
a) Hàm \(v(t) = 3{t^2} - 12t + 9\).
b) Hàm \(a(t) = 6t - 12\).
c) Trong khoảng từ \[t = 0\] đến \(t = 2\) thì vận tốc của chất điểm tăng.
d) Từ \(t = 2\) trở đi thì vận tốc của chất điểm giảm.
Cho hàm số \(y = x + \frac{4}{x}\).
a) Đạo hàm của hàm số đã cho là \(y' = 1 + \frac{4}{{{x^2}}}\).
b) Đạo hàm của hàm số đã cho nhận giá trị âm trên các khoảng \(\left( { - 2;\,0} \right) \cup \left( {0;\,2} \right)\) và nhận giá trị dương trên các khoảng \(\left( { - \infty ;\, - 2} \right) \cup \left( {2;\, + \infty } \right)\).
c) Bảng biến thiên của hàm số đã cho là:
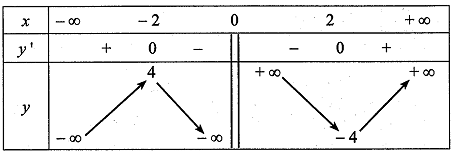
d) Đồ thị hàm số đã cho như hình
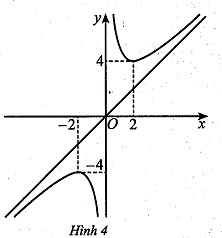
Phần III. Trắc nghiệm trả lời ngắn
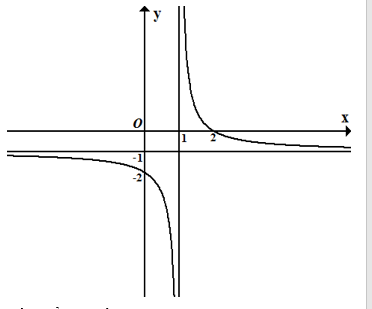
Cho hàm số \(y = \frac{{ax + b}}{{x + c}}\) có đồ thị như hình bên dưới, với \(a\), \(b\), \(c \in \mathbb{Z}\). Tính giá trị của biểu thức \(T = a + 2b + 3c\).
Đồ thị trong hình bên dưới là của hàm số \(y = \frac{{ax + b}}{{x + c}}\) (với \(a,b,c \in \mathbb{R}\)).
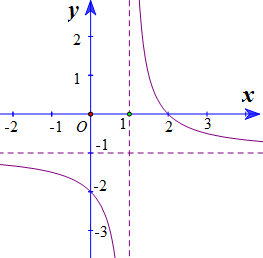
Tính\(a + b + c\).
Đồ thị trong hình bên dưới là của hàm số \(y = ax + b + \frac{1}{{x + c}}\).
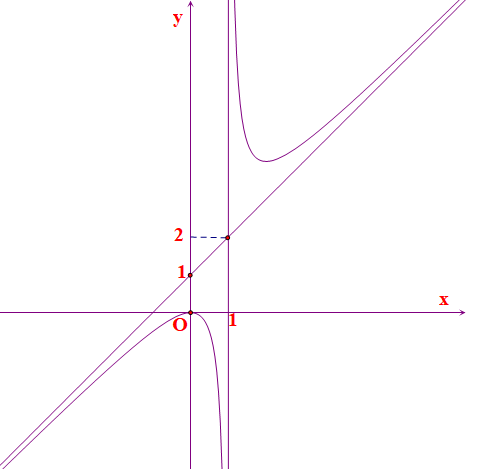
Tính \(a + b + c\).
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{x + d}}(a,b,c,d \in \mathbb{R})\) có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số \(a,b,c,d\)?
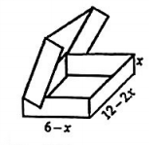
Một hộp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên của hộp được rải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi \(x = {x_0}\) là giá trị làm cho hộp kim loại có thể tích lớn nhất. Khi đó thể tích chocolate nguyên chất có giá trị là bao nhiêu?