Đề cương ôn tập cuối kì 1 Toán 12 Chân trời sáng tạo (có tự luận) có đáp án - Bài 1. Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm
11 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Kết quả khảo sát cân nặng của 1 thùng táo ở một lô hàng cho trong bảng sau:
Cân nặng (g) | \(\left[ {150;\,155} \right)\) | \(\left[ {155;\,160} \right)\) | \(\left[ {160;\,165} \right)\) | \(\left[ {165;\,170} \right)\) | \(\left[ {170;\,175} \right)\) |
Số quả táo | \(4\) | \(7\) | \(12\) | \[6\] | \(2\) |
Khoảng biến thiên \(R\) của mẫu số liệu ghép nhóm trên là.
\(R = 5\).
\(R = 24\).
\(R = 25\).
\(R = 10\).
Bạn Linh thống kê chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp \(12A\) và lớp \(12\,B\) ở bảng sau:
Chiều cao (cm) | \(\left[ {150;155} \right)\) | \(\left[ {155;160} \right)\) | \(\left[ {160;165} \right)\) | \(\left[ {165;170} \right)\) | \(\left[ {170;175} \right)\) | \(\left[ {175;180} \right)\) |
Số học sinh nữ lớp 12 A | 2 | 7 | 12 | 3 | 0 | 1 |
Số học sinh nữ lớp 12 B | 0 | 9 | 8 | 2 | 1 | 5 |
Gọi \({R_1}\); \({R_2}\)lần lượt là khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp \(12A\) và \(12\,B\). Tìm \({R_1}\); \({R_2}\).
\({R_1} = 30\,\,\left( {{\rm{cm}}} \right)\,;\,\,{R_2} = 25\,\,\left( {{\rm{cm}}} \right)\).
\({R_1} = 30\,\,\left( {{\rm{cm}}} \right)\,;\,\,{R_2} = 30\,\,\left( {{\rm{cm}}} \right)\).
\({R_1} = 25\,\,\left( {{\rm{cm}}} \right)\,;\,\,{R_2} = 25\,\,\left( {{\rm{cm}}} \right)\).
\({R_1} = 12\,\,\left( {{\rm{cm}}} \right)\,;\,\,{R_2} = 9\,\,\left( {{\rm{cm}}} \right)\).
Số lượng đặt bàn của một nhà hàng được cho bởi bảng sau:
Số lượt đặt bàn | Tần số | Tần số tích lũy |
[1; 6) | 14 | 14 |
[6; 11) | 30 | 44 |
[11; 16) | 25 | 69 |
[16; 21) | 18 | 87 |
[21; 26) | 5 | 92 |
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi bảng trên.
\({\Delta _Q} = \frac{{11}}{6}\).
\[{\Delta _Q}\; = \frac{{17}}{2}\].
\({\Delta _Q} = \frac{5}{2}\).
\({\Delta _Q} = \frac{{17}}{6}\).
Gọi \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của một mẫu số liệu ghép nhóm. Khi đó khoảng tứ phân vị \({\Delta _Q}\) của mẫu số liệu trên được xác định bởi công thức
\[{\Delta _Q}\; = {Q_2} - {Q_1}\].
\[{\Delta _Q}\; = {Q_3} - {Q_1}\].
\[{\Delta _Q}\; = {Q_2} - {Q_3}\].
\[{\Delta _Q}\; = {Q_1} - {Q_3}\].
Điều tra về khối lượng \[27\] củ khoai tây (đơn vị: gam) thu hoạch tại nông trường, ta có kết quả sau:
Nhóm | Tần số |
\(\left[ {74;\;80} \right)\) | \(4\) |
\(\left[ {80;\;86} \right)\) | \(6\) |
\(\left[ {86;\;92} \right)\) | \(3\) |
\(\left[ {92;\;98} \right)\) | \(4\) |
\(\left[ {98;\;104} \right)\) | \(3\) |
\(\left[ {104;\;110} \right)\) | \(7\) |
| \[n = 27\] |
Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên lần lượt là
\(36;\,\,21,45\).
\(7;\,\,23\).
\(11;\,\,\,25,3\).
\(33;\,\,20,5\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Thời gian tập đàn mỗi ngày (tính theo phút) của bạn Thu trong thời gian gần đây được thống kê như sau:
Nhóm | Tần số |
\[\left[ {20;25} \right)\] | \[6\] |
\[\left[ {25;30} \right)\] | \[5\] |
\[\left[ {30;35} \right)\] | \[7\] |
\[\left[ {35;40} \right)\] | \[8\] |
\[\left[ {40;45} \right)\] | \[2\] |
a)Khoảng biến thiên của mẫu số liệu ghép nhóm là \[R = 25\].
b)Nhóm chứa tứ phân vị thứ nhất là nhóm \[\left[ {20;25} \right)\].
c)Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \[{Q_3} = 37\].
d)Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \[{\Delta _Q} = \frac{{87}}{8}\].
Bạn Trang thống kê lại chiều cao (đơn vị cm) của các bạn học sinh nữ lớp 12C và 12D ở bảng sau.
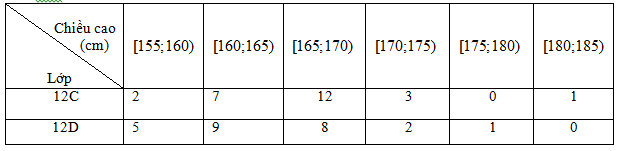
a)Chiều cao cao nhất của các bạn học sinh trong lớp 12D là 185(cm).
b) Khoảng biến thiên của chiều cao của các bạn học sinh nữ lớp 12C là 30(cm).
c) Khoảng biến thiên của chiều cao các bạn học sinh nữ lớp 12D là 25(cm).
d)Chiều cao của học sinh lớp 12C có độ phân tán bé hơn.
Bảng sau biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị:triệu đồng)
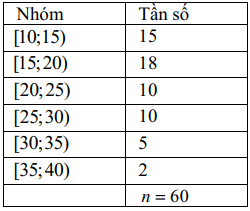
a)Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \[R = 30\].
b) Số phần tử của mẫu là \[n = 60\].
c) Tứ phân vị thứ nhất là \[{Q_1} = 15\].
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \[{\Delta _Q} = 3\].
Phần III. Trắc nghiệm trả lời ngắn
Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau:
Tuổi thọ (ngày) | \(\left[ {0\,;20} \right)\) | \(\left[ {20\,;40} \right)\) | \(\left[ {40\,;60} \right)\) | \(\left[ {60\,;80} \right)\) | \(\left[ {80\,;100} \right)\) |
Số lượng | 5 | 12 | 23 | 31 | 29 |
Tìm khoảng tứ phân vị của mẫu số liệu (làm tròn kết quả đến hàng phần mười).
Một cửa hàng trang sức khảo sát khách hàng xem họ dự định mua trang sức với mức giá nào (đơn vị: triệu đồng). Kết quả khảo sát được ghi lại ở bảng sau:
Mức giá | \([6;9)\) | \([9;12)\) | \([12;15)\) | \([15;18)\) | \([18;21)\) |
Số khác hàng | 20 | 78 | 45 | 23 | 12 |
Tìm khoảng biến thiên của mẫu số liệu ghép nhóm.
Khảo sát thời gian (phút) tập thể dục trong ngày của một số học sinh lớp 12 thu được mẫu số liệu ghép nhóm sau:

Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần mười).