Đề cương ôn tập giữa kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 3. Đường tiệm cận của đồ thị hàm số
18 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho hàm số \[y = f(x)\] xác định trên \[\mathbb{R}\backslash \left\{ 0 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
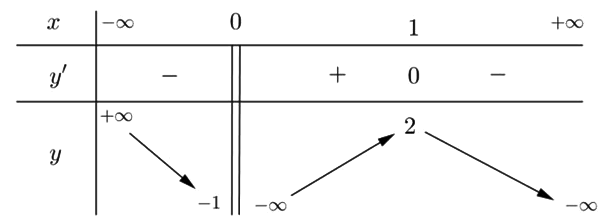
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận?
0.
1.
2.
3
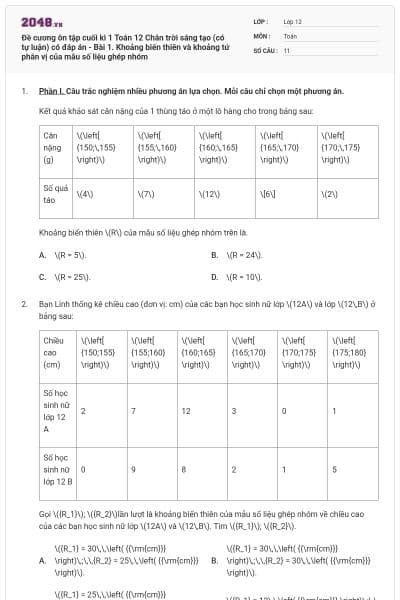
Hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ dưới đây.
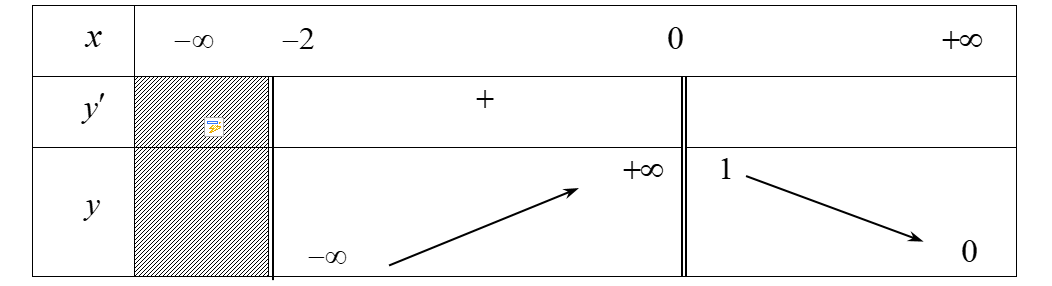
Cho các khẳng định sau:
(1) Đồ thị hàm số có tiệm cận đứng \(x = - 2.\)
(2) Hàm số đạt giá trị cực đại tại \(x = 0.\)
(3) Hàm số đồng biến trên \(\left( { - 2;\,0} \right)\).
(4) Hàm số có tiệm cận ngang \(y = 1.\)
Số khẳng định đúng là:
1.
4.
2.
0.
Hàm số \(y = f\left( x \right)\) liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ dưới đây.
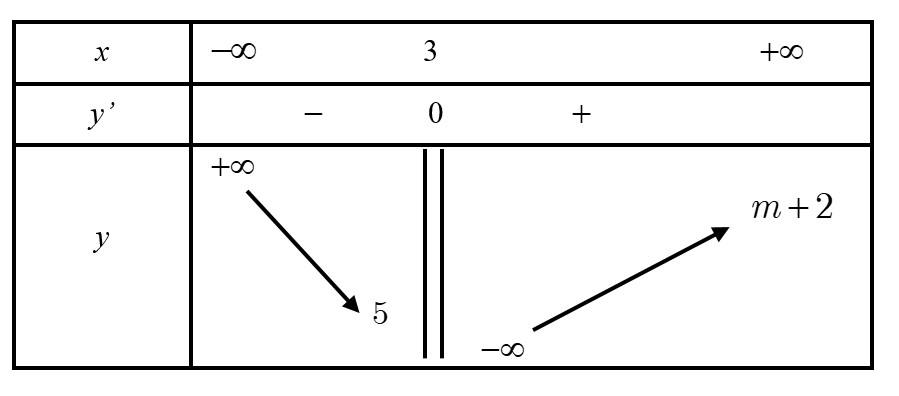
Tìm m để \[\mathop {\lim }\limits_{x\, \to \, + \infty } \,f\left( x \right)\, < 10.\]
\(m < 1\).
\(m < 10\).
\(m < 8\).
\(m > 8\)
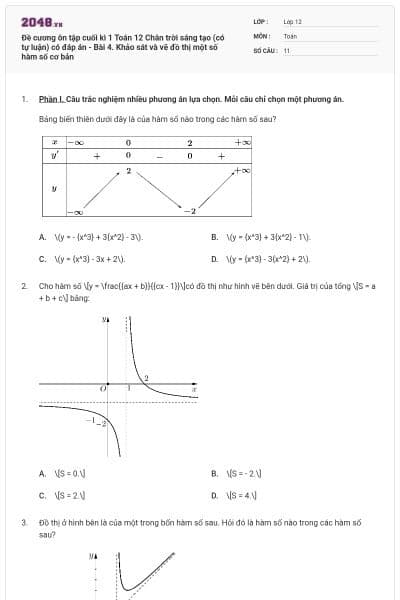
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau:

Tìm tổng số các giá trị nguyên dương của tham số \(m \in \left( { - 10\,;\,10} \right)\) để đồ thị hàm số \(y = f\left( x \right)\) có tổng số đường tiệm cận đứng và đường tiệm cận ngang là \(4\).
\(42\).
\(45\).
\( - 3\).
\(0\).
Đường thẳng \[y = - 1\]là tiệm cận ngang của đồ thị hàm số nào sao đây?
\(y = \frac{{1 + x}}{{1 - x}}\).
\[y = \frac{{x - 2}}{{x + 2}}\].
\[y = \frac{{ - {x^2} + 2}}{{x + 1}}\].
\[y = \frac{{ - 1 - x}}{{1 - x}}\].
Cho hàm số \(y = \frac{{3x - 1}}{{x + 1}}\). Chọn phát biểu đúng?
Đồ thị hàm số có \(y = 3\) là tiệm cận đứng.
Giao điểm hai tiệm cận là \(\left( {3; - 1} \right)\).
Đồ thị có tiệm cận đứng có phương trình là \(x + 1 = 0\).
Hai tiệm cận tạo với hai trục tọa độ một hình vuông có diện tích là 3.
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ dưới. Chọn khẳng định sai.
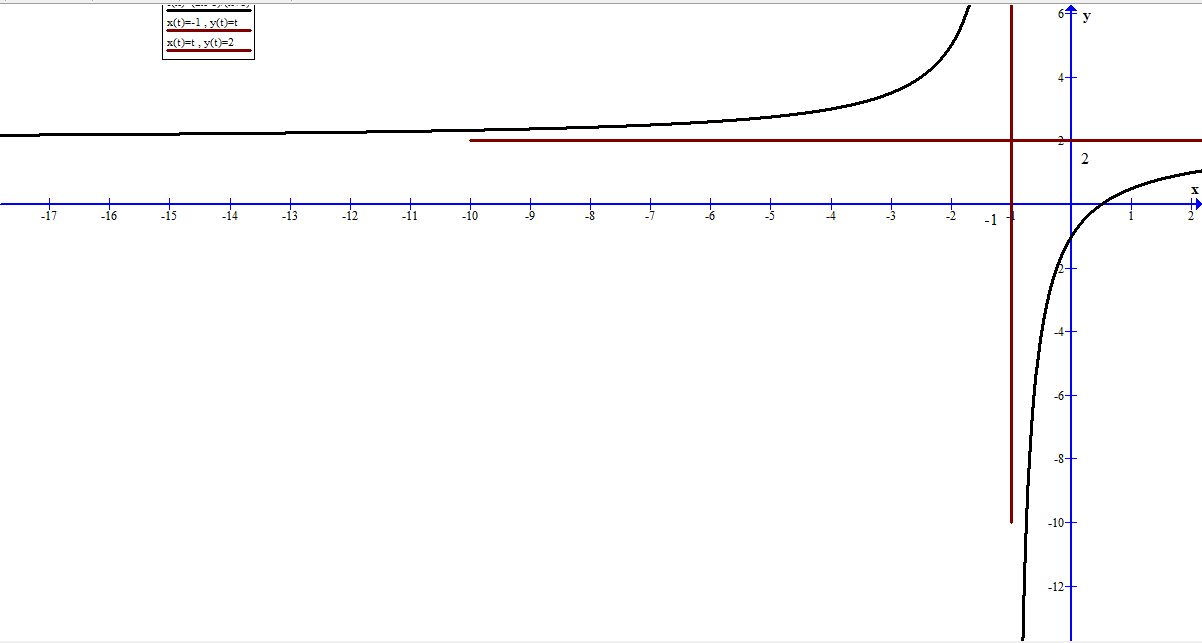
Đồ thị hàm số có tiệm cận đứng \(x = - 1.\)
Đồ thị hàm số có tiệm cận ngang \(y = 2.\)
Đồ thị hàm số có tâm đối xứng là \(I\left( {2; - 1} \right)\).
Đồ thị hàm số có hai đường tiệm cận.
Hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
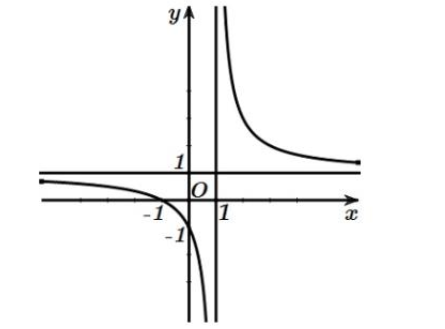
\(y = \frac{{2 - x}}{{x - 1}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = \frac{{x - 2}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
Đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = x + 3 + \frac{1}{{2x + 1}}\) có phương trình là
\(y = 2x + 1\).
\(y = x - 3\).
\(y = x + 3\).
\(y = 2x - 1\).
Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} + 3x}}{{x - 2}}\).
\(y = 2x - 5\).
\(y = x - 2\).
\(y = x + 5\).
\(y = x - 5\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới
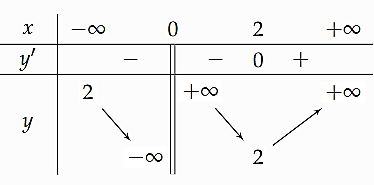
a) \(f\left( { - 5} \right) < f\left( 4 \right)\).
b) Hàm số có giá trị nhỏ nhất bằng 2.
c) Đồ thị hàm số có tiệm cận đứng \(x = 0\).
d) Đồ thị hàm số không có tiệm cận ngang.
Cho hàm số \(y = \frac{{2x - 3}}{{ - x + 1}}\).
a) Bảng biến thiên của hàm số là
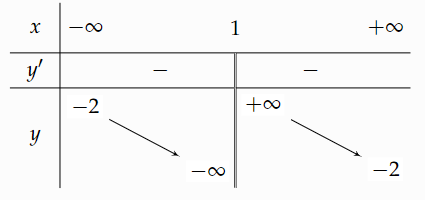
b) Tâm đối xứng của đồ thị hàm số là \(I\left( {1; - 2} \right)\).
c) Đường tiệm cận đứng của đồ thị hàm số là \(x = - 2\).
d) Đường tiệm cận ngang của hàm số là \(y = 1\).
Cho đồ thị hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\).
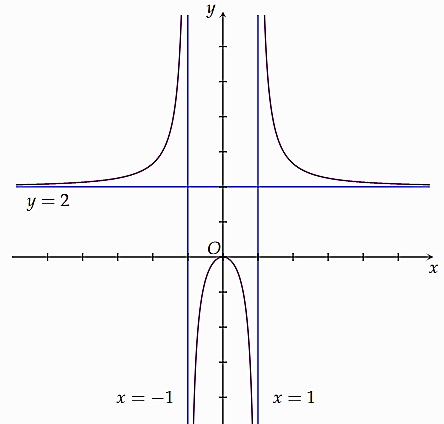
a) Đồ thị hàm số có 3 điểm cực trị.
b)\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2;\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \).
c) Đồ thị hàm số có 3 đường tiệm cận đứng là \(x = - 1;x = 0;x = 1\).
d) Đồ thị hàm số có hai đường tiệm cận ngang \(y = 2\) và \(y = 0\).
Cho hàm số \[y = f\left( x \right)\] xác định và có đạo hàm trên \[\mathbb{R}\backslash \left\{ { \pm 2} \right\}\]. Hàm số \[f\left( x \right)\] có bảng biến thiên như hình vẽ dưới đây
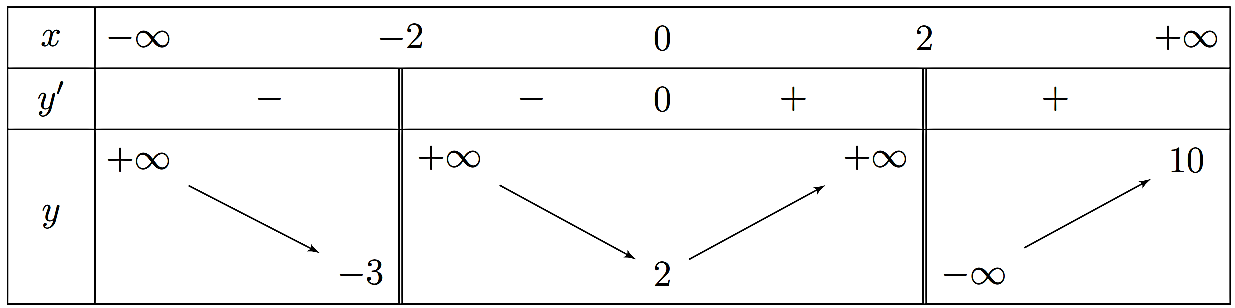
a) Đường tiệm cận ngang của đồ thị hàm số \[y = f\left( x \right)\]là đường thẳng \(y = 10\).
b) Một đường tiệm cận đứng của đồ thị hàm số \[y = f\left( x \right)\]là đường thẳng \(x = - 3\).
c) Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = f\left( x \right)\]là 3.
d) Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = \frac{1}{{2f\left( x \right) + 6}}\] là 4.
Cho hàm số \(y = \frac{{x - 1}}{{x + 1}}\) có đồ thị (C). Khi đó:
a) Đạo hàm hàm số là \(y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}}\).
b) Tiệm cận ngang của đồ thị hàm số là y = 1.
c) Tâm đối xứng của đồ thị hàm số là \(\left( {1; - 1} \right)\).
d) Với mọi \(M \in \left( C \right)\) tích khoảng cách từ M đến các đường tiệm cận bằng 3.
Phần III. Trắc nghiệm trả lời ngắn
Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}\). Khi đó \(a + b\) bằng bao nhiêu để đồ thị của hàm số trên nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = \frac{1}{2}\) làm tiệm cận ngang.
Có bao nhiêu giá trị của tham số thực m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng hai đường tiệm cận?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ
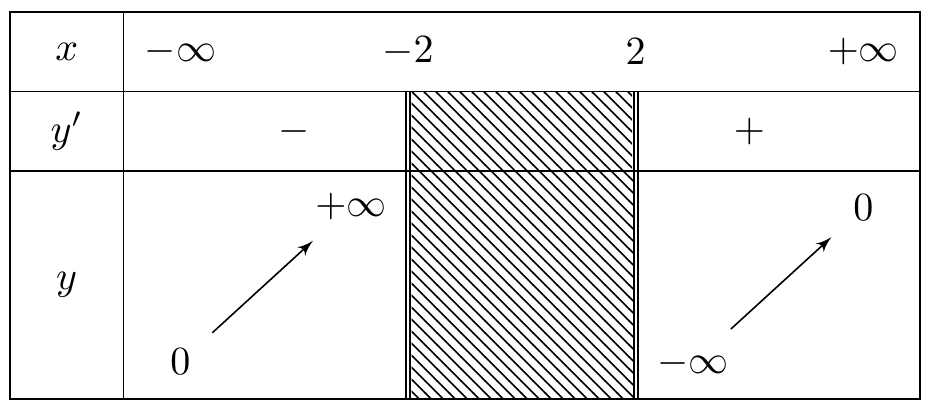
Tính tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số.