Đề cương ôn tập giữa kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
20 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Giá trị nhỏ nhất của hàm sốcó bảng biến thiên sau trên khoảng \(\left[ { - 2;3} \right]\) là:
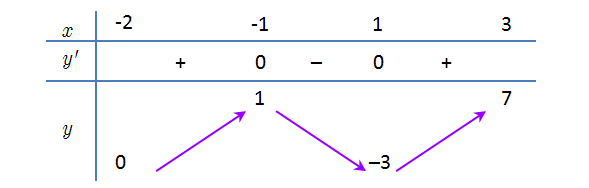
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = 0\].
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = - 3\].
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = 1\].
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = 7\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 5;\,3} \right)\) và có bảng biến thiên như sau
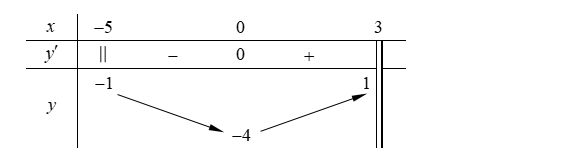
Mệnh đề nào sau đây đúng?
Hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất và không có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất và có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất và có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục và có bảng biến thiên trong đoạn \(\left[ { - 2;\,4} \right]\) như sau
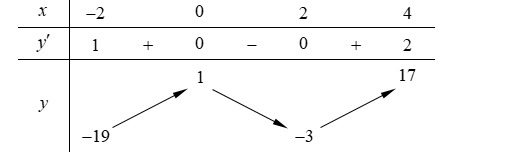
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;\,4} \right]\) bằng
\[ - 19\].
1.
\[ - 3\].
\[17\].
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là:
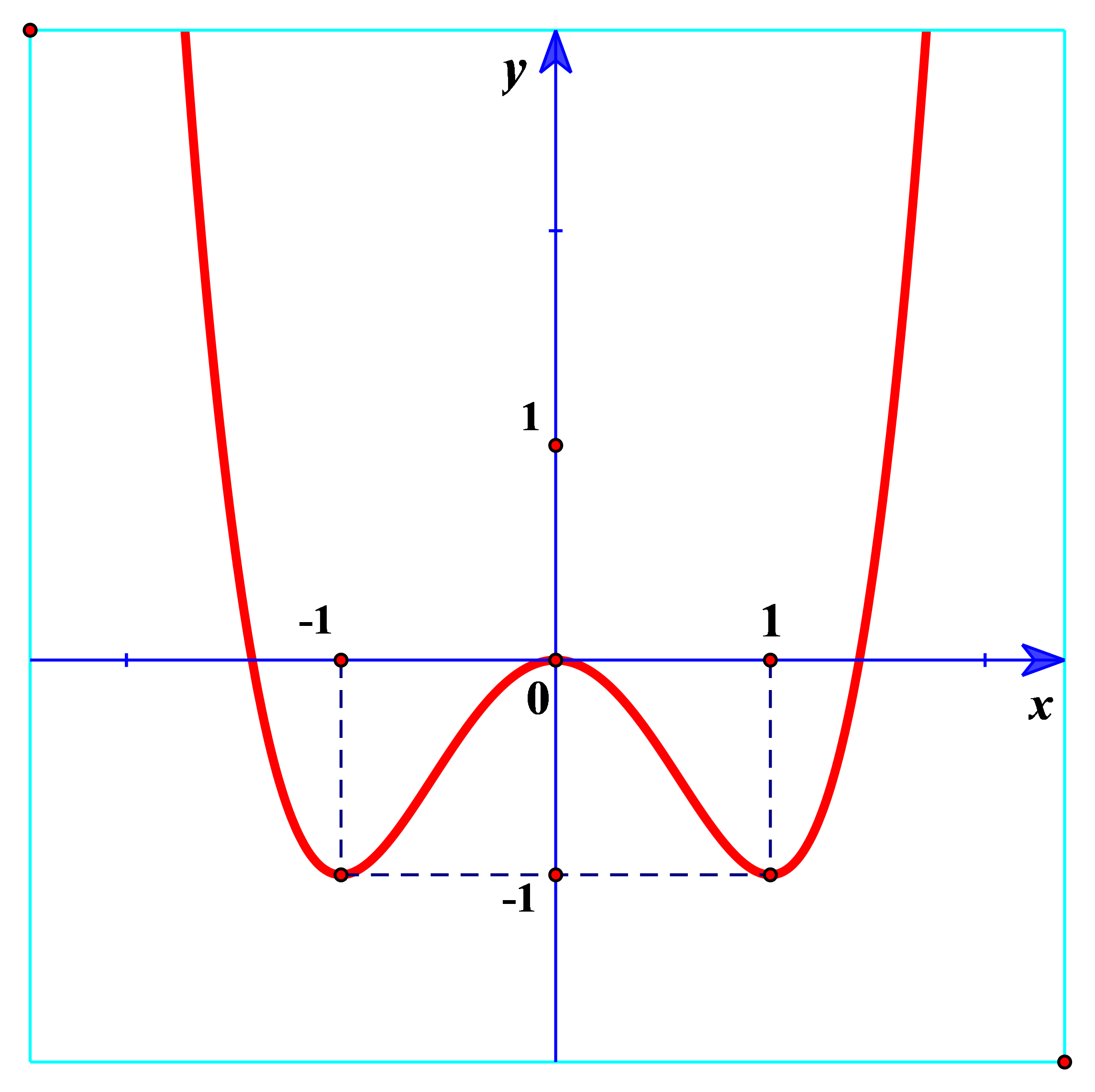
\[\mathop {\min }\limits_{} y = - 1.\]
\[\mathop {\min }\limits_{} y = 1\].
\[\mathop {\min }\limits_{} y = 0\].
\[\mathop {\min }\limits_{} y = - 2\].
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = {x^3} - 3{x^2} - 9x + 2\] trên \[\left[ { - 2;\,2} \right]\] lần lượt là:
7 và 2.
7 và \[ - 1\].
7 và 0.
7 và \[ - 20\].
Giá trị nhỏ nhất của hàm \(y = {e^{{x^2} - 2x}}\) trên đoạn \(\left[ {0;2} \right]\) là
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = 1\).
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = e\).
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = \frac{1}{{{e^2}}}\).
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = \frac{1}{e}\).
Gọi giá trị lớn nhất, nhỏ nhất của hàm số \[y = x - 5 + \frac{1}{x}\] trên khoảng \[\left( {0; + \infty } \right)\] là \[M;m\]. Khi đó, các giá trị \[M;m\]lần lượt là :
Không có \(M\); \[m = - 3\].
\[M = - 3\]; \[m = 1\].
\[M = 0\]; \[m = 1\].
Không có \[M;m\].
Cho đồ thị hàm số \(y = f'(x)\) như hình vẽ.
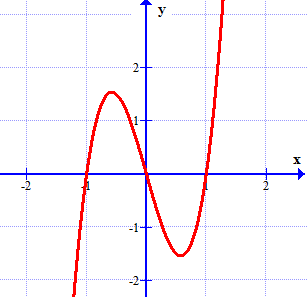
Hàm số \(y = f(x)\) đạt giá trị nhỏ nhất trên khoảng \(\left[ {0;2} \right]\) tại \[x\] bằng bao nhiêu?
\[x = \frac{2}{3}\].
\[x = 0\].
\[x = 1\].
\[x = 2\].
Cho đồ thị hàm số \(y = f'(x)\) như hình vẽ.
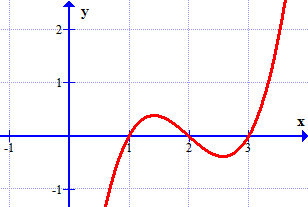
Hàm số \(y = f(x)\) đạt giá trị lớn nhất trên khoảng \(\left[ {1;3} \right]\) tại \[{x_0}\]. Khi đó giá trị của \[x_0^2 - 2{x_0} + 2018\] bằng bao nhiêu?
\[2018\].
\[2017\].
\[2021\].
\[2026\].
Một chất điểm chuyển động theo quy luật \(s\left( t \right) = {t^2} - \frac{1}{6}{t^3}\left( {\rm{m}} \right).\) Tìm thời điểm \(t\) (giây) mà tại đó vận tốc \(v\left( {{\rm{m/s}}} \right)\) của chuyển động đạt giá trị lớn nhất.
\(t = 2\).
\(t = 0,5\).
\(t = 2,5\).
\(t = 1\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = {x^3} - 3{x^2} + 1\).
a) Hàm số đồng biến trên khoảng \(\left( {3; + \infty } \right)\).
b) Hàm số đạt cực tiểu tại \(x = - 3\).
c) Hàm số đạt giá trị lớn nhất trên đoạn \(\left[ {1;3} \right]\) tại \(x = 1\).
d) Đồ thị hàm số đối xứng qua điểm \(I\left( {1; - 1} \right)\).
Cho hàm số \(y = {x^3} - 3{x^2} - 9x + 1\).
a) Hàm số đồng biến trên khoảng \(\left( { - 26; + \infty } \right)\).
b) Hàm số đạt cực đại tại \(x = - 1\).
c) Giá trị nhỏ nhất của hàm trên \(\left( { - 1; + \infty } \right)\) là −26.
d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho là \(4\sqrt {65} \).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị của hàm số \(f'\left( x \right)\) trên đoạn \(\left[ { - 2;6} \right]\) như hình vẽ bên dưới.
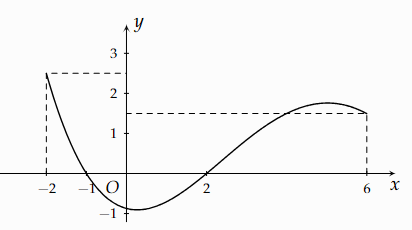
a) \(\mathop {\max }\limits_{\left[ { - 2;6} \right]} f\left( x \right) = f\left( { - 1} \right)\).
b)\(\mathop {\max }\limits_{\left[ { - 2;6} \right]} f\left( x \right) = f\left( 6 \right)\).
c)\(\mathop {\max }\limits_{\left[ { - 2;6} \right]} f\left( x \right) = f\left( { - 2} \right)\).
d)\(\mathop {\max }\limits_{\left[ { - 2;6} \right]} f\left( x \right) = \max \left\{ {f\left( { - 1} \right),f\left( 6 \right)} \right\}\).
Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được \(x\) mét vải lụa \((1 \le x \le 18)\). Tổng chi phí sản xuất \(x\) mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:\(C(x) = {x^3} - 3{x^2} - 20x + 500.\) Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng/mét. Gọi \(B(x)\) là số tiền bán được và \(L(x)\) là lợi nhuận thu được khi bán \(x\) mét vải lụa.
a) Biểu thức tính \(B(x)\) theo \(x\) là \(B(x) = 220x\)(nghìn đồng).
b) Biểu thức tính \(L(x)\) theo \(x\)là \(L(x) = - {x^3} + 3{x^2} + 220x - 500\) (nghìn đồng).
c) Hộ làm nghề dệt này cần sản xuất và bán ra mỗi ngày 10 mét vải lụa để thu được lợi nhuận tối đa.
d) Lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm có thể đạt được là 1000 nghìn đồng.
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị bên dưới. Gọi \[M,{\rm{ }}m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {1\,;\,3} \right]\].
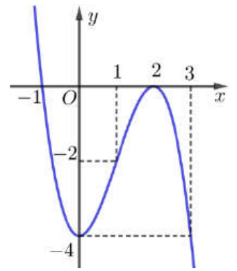
a)\(m = - 4\).
b) \(M = - 2\).
c) \(M + m = - 4\).
d)Giá trị lớn nhất của hàm số \(y = f\left( x \right) + 4\) trên nửa khoảng \(\left[ { - 1\,;\, + \infty } \right)\) là \(0\).
Phần III. Trắc nghiệm trả lời ngắn
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số\(f(t) = \frac{{5000}}{{1 + 5{e^{ - t}}}},t \ge 0,\)trong đó thời gian \(t\) được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm \(f'(t)\) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất? (kết quả làm tròn đến hàng phần mười).
Có bao nhiêu giá trị m để giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{x - {m^2} + m}}{{x + 1}}\) trên đoạn \(\left[ {0;1} \right]\) bằng \( - 2\)?
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số \(N\left( t \right) = - {t^3} + 12{t^2},0 \le t \le 12\), trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần). Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.
Hộp sữa 1 lít được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh \(x\) cm. Tìm \(x\) để diện tích toàn phần của hộp nhỏ nhất.
Ông A muốn mua một mảnh đất hình chữ nhật có diện tích bằng \(100\,{{\rm{m}}^{\rm{2}}}\)để làm khu vườn. Để chi phí xây dựng bờ rào xung quanh khu vườn là ít tốn kém nhất thì ông A đã mua mảnh đất có kích thước \(a({\rm{m}})\, \times \,b({\rm{m}})\)(với \(a\) là chiều dài, \(b\) là chiều rộng của khu vườn). Khi đó kết quả của \(a + 2b\) bằng bao nhiêu?