Đề cương ôn tập giữa kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 1. Tính đơn điệu và cực trị của hàm số
20 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tìm khoảng đồng biến của hàm số: \[y = - {x^4} + 4{x^2} - 3\].
\((0; + \infty )\).
\(( - \infty ;0)\).
\(( - \infty ; - \sqrt 2 )\)và \((0;\sqrt 2 )\).
\((\sqrt 2 ; + \infty )\).
Tìm khoảng nghịch biến của hàm số: \[y = \frac{{3 - 2x}}{{x + 7}}\].
\(( - \infty ;7)\).
\(( - \infty ; + \infty )\).
\(( - \infty ; - 7)\)và \(( - 7; + \infty )\).
\(( - 10; + \infty )\).
Hàm số \(y = \sqrt {2x - {x^2}} \) nghịch biến trên khoảng nào.
\(\left( {0;1} \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( {1;2} \right)\).
\(\left( {1; + \infty } \right)\).
Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
\[y = \frac{{x - 1}}{{x + 2}}\].
\[y = {x^3} + 4{x^2} + 3x--1\].
\[y = {x^4}--2{x^2}--1\].
\[y = \frac{1}{3}{x^3} - \frac{1}{2}{x^2} + 3x + 1\].
Cho các hàm số sau:
\(\left( I \right):y = - {x^3} + 3{x^2} - 3x + 1;\left( {II} \right):y = \sin x - 2x;\)\(\left( {III} \right):y = - \sqrt {{x^3} + 2} ;\left( {IV} \right):y = \frac{{x - 2}}{{1 - x}}\).
Hỏi hàm số nào nghịch biến trên toàn trục số?
(I), (II).
(I), (II) và (III).
(I), (II) và (IV).
(II), (III).
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Hỏi điểm cực tiểu của đồ thị hàm số \[y = f\left( x \right)\]là điểm nào?
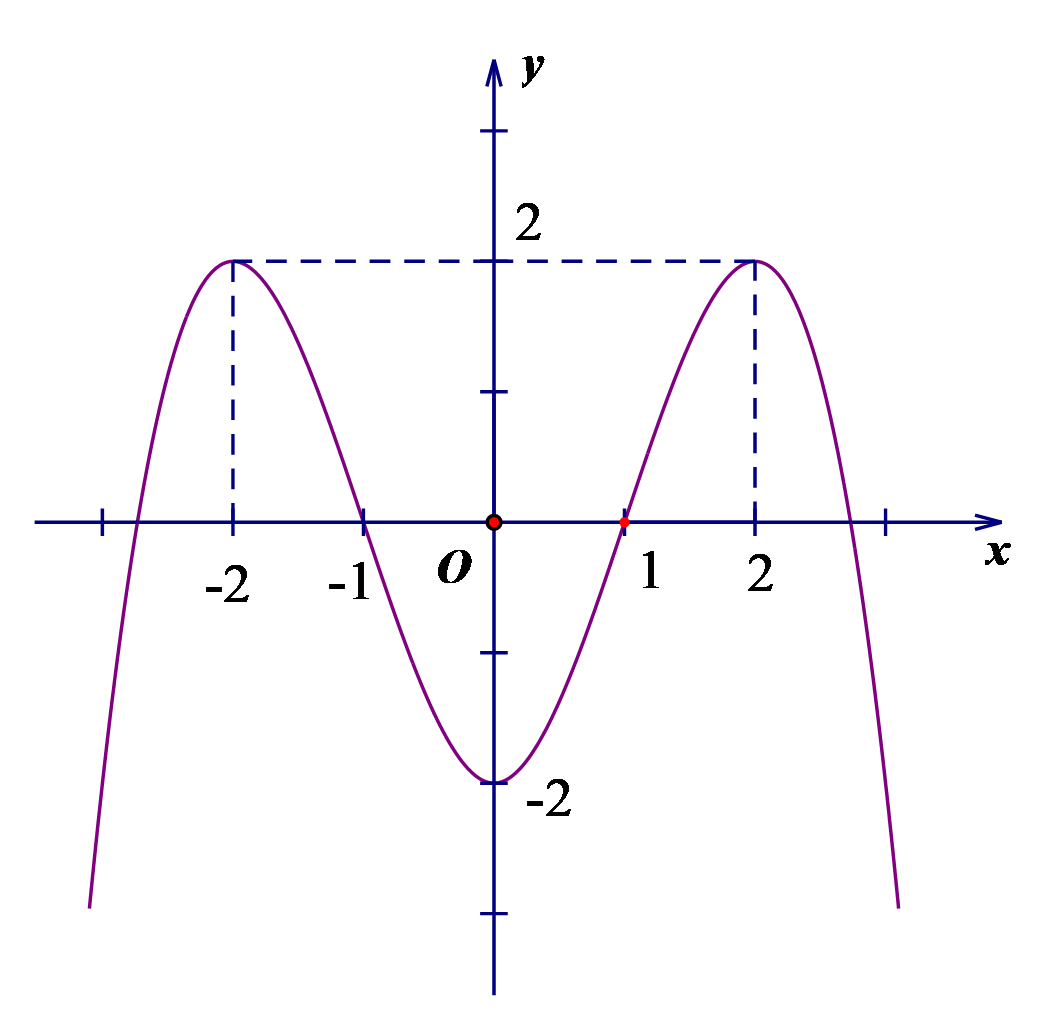
\[x = - 2.\]
\[y = - 2.\]
\[M\left( {0; - 2} \right).\]
\[N\left( {2\,;2} \right).\]
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {0;4} \right]\) có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
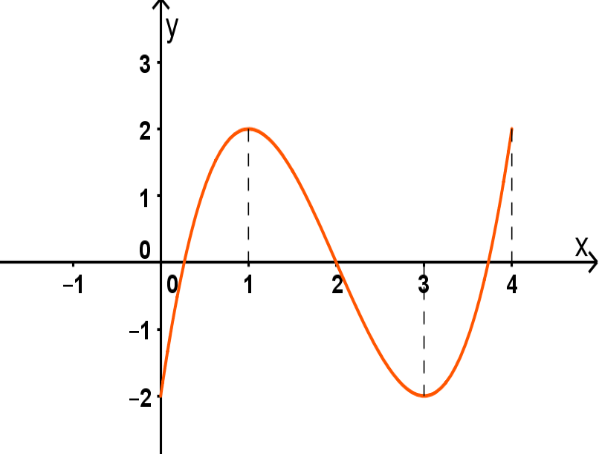
Hàm số đạt cực đại tại \(x = 4.\)
Hàm số đạt cực tiểu tại \(x = 0.\)
Hàm số đạt cực đại tại \(x = 2.\)
Hàm số đạt cực tiểu tại \(x = 3.\)
Gọi \(M,n\) lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) . Khi đó giá trị của biểu thức \({M^2} - 2n\) bằng:
8.
7.
9.
6.
Hàm số nào sau đây không có cực trị?
\(y = 2x + \frac{2}{{x + 1}}.\)
\(y = {x^3} + 3{x^2}.\)
\(y = - {x^4} + 2{x^2} + 3.\)
\(y = \frac{{x + 1}}{{x - 2}}.\)
Cho hàm số \(y = f(x)\)có bảng biến thiên như sau:
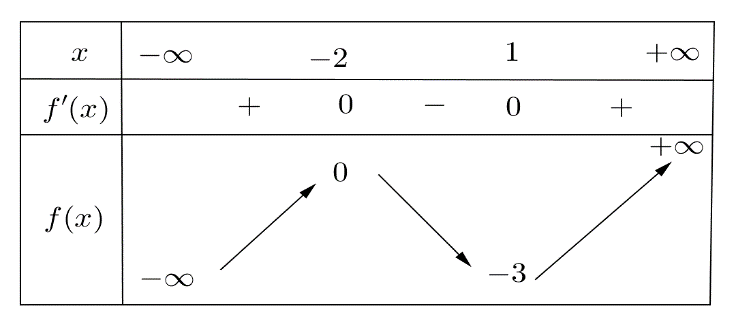
Giá trị cực tiểu của hàm số đã cho là:
\( - 2\).
\(1\).
\( - 3\) .
\(0\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

a) Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
b) Hàm số đồng biến trên khoảng \(\left( { - 2;0} \right)\).
c) Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).
d) Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Cho hàm số \(y = \frac{{x + 3}}{{x + 2}}\).
a) Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).
b) Hàm số nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
c) Hàm số đồng biến trên \(\mathbb{R}\).
d) Hàm số nghịch biến trên \(\left( { - 4; - 3} \right)\).
Cho hàm số \(y = {x^4} - 2{x^2} + 1\).
a) Hàm số có 3 điểm cực trị.
b) Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
c) Hàm số có 1 điểm cực trị.
d) Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
Cho hàm số \(y = \sqrt {8 + 2x - {x^2}} \).
a) Tập xác định của hàm số là \(D = \left[ { - 2;4} \right]\).
b) Hàm số có \(y' = \frac{{1 - x}}{{\sqrt {8 + 2x - {x^2}} }}\).
c) Hàm số nghịch biến trên khoảng \(\left( {1;4} \right)\).
d) Giá trị cực đại của hàm số là 0.
Cho hàm số bậc ba \(y = f(x)\) có đồ thị là đường cong như hình vẽ sau
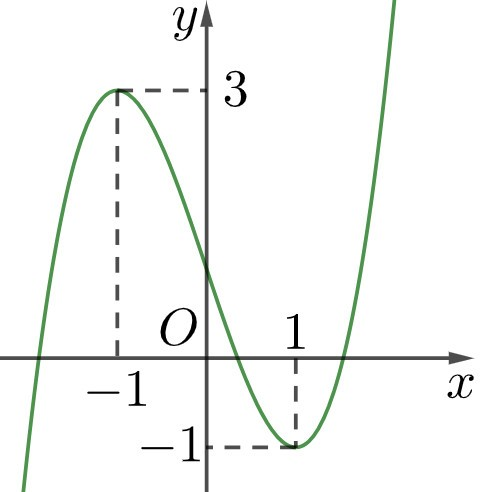
a) Hàm số \(y = f(x)\)đồng biến trên khoảng \(( - \infty ;3).\)
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số là 2.
c) Hàm số \(y = f(x)\)có hai cực trị trái dấu.
d) Phương trình đường thẳng qua 2 điểm cực trị của đồ thị hàm số \(y = f(x)\) là \[d:y = - 3x\].
Phần III. Trắc nghiệm trả lời ngắn
Cho hàm số \(y = f\left( x \right) = {x^3} + 2{x^2} + x - 3\) đạt cực tiểu tại \(x = a\), cực đại tại \(x = b\). Tính\(3a + 6b\).
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số \(N\left( t \right) = - {t^3} + 12{t^2},0 \le t \le 12\), trong đó N là số người bị nhiễm bệnh (đơn vị là trăm người) và t là thời gian (tuần). Gọi \(\left( {a;b} \right)\) là khoảng thời gian lâu nhất mà số người bị nhiễm bệnh tăng lên. Tính\(P = 2{a^2} - {b^2}.\)
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó t là thời gian tính bằng giây. Hỏi thời gian bằng bao nhiêu để số lượng vi khuẩn đạt cực đại.
Một chất điểm chuyển động theo phương trình \(s\left( t \right) = - \frac{{{t^3}}}{3} + 18{t^2} - 35t + 10\), trong đó \(t\) tính bằng giây và \(s\)tính bằng mét. Trong 40 giây đầu tiên, chất điểm có vận tốc tức thời giảm trong khoảng thời gian \(\left( {a;b} \right)\). Tính giá trị của biểu thức \(P = 2b - 3a\).
Hằng ngày mực nước của một con kênh lên xuống theo thủy triều. Độ sâu \(h\,\,\left( {\rm{m}} \right)\) của mực nước trong kênh tại thời điểm \(t\,\,\left( {\rm{h}} \right)\,\,\left( {0 \le t \le 24} \right)\) trong ngày được xác định bởi công thức \(h = 2\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 5\). Gọi \(\left( {a\,;\,b} \right)\) là khoảng thời gian trong ngày mà độ sâu của mực nước trong kênh tăng dần. Tính giá trị của \(a + b\).