Đề cương ôn tập giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Bài 9: Các số đặc trưng đo xu thế trung tâm
31 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa mốtcủamẫu số liệutrênlà
\[[40;60)\].
\[[20;40)\].
\[[60;80)\].
\[[80;100)\].
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa tứ phân vị thứ bacủamẫu số liệutrênlà
\[[40;60)\].
\[[20;40)\].
\[[60;80)\].
\[[80;100)\].
Doanhthubánhàngtrong20ngàyđượclựachọn ngẫu nhiêncủamột củahàngđượcghilạiởbảngsau(đơnvị:triệu đồng)

Sốtrungbìnhcủamẫu số liệutrênthuộckhoảngnàotrongcáckhoảngdướiđây?
\[\left[ {7;{\rm{ }}9} \right)\].
\[\left[ {9;{\rm{ }}11} \right)\].
\[\left[ {11;{\rm{ }}13} \right)\].
\[\left[ {13;{\rm{ }}15} \right)\].
Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Số trung vị của mẫu số liệu ghép nhóm ở bảng trên là
\[18,1\].
\[18,2\].
\[18,3\].
\[18,4\] .
Doanhthubánhàngtrong20ngàyđượclựachọn ngẫu nhiêncủamột củahàngđượcghilạiởbảngsau(đơnvị:triệu đồng):

Tứ phânvị thứ nhấtcủamẫu số liệugần nhất với giá trị nào trong các giá trịdướiđây?
\[7\].
\[7,6\].
\[8\].
\[8,6\].
Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
Thời gian | \(\left[ {15;20} \right)\) | \(\left[ {20;25} \right)\) | \(\left[ {25;30} \right)\) | \(\left[ {30;35} \right)\) | \(\left[ {35;40} \right)\) | \(\left[ {40;45} \right)\) | \(\left[ {45;50} \right)\) |
Số nhân viên | 7 | 14 | 25 | 37 | 21 | 14 | 10 |
Tứ phân vị thứ nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm này là
\({Q_1} = \frac{{1360}}{{37}},{Q_3} = \frac{{800}}{{21}}\).
\({Q_1} = \frac{{1360}}{{37}},{Q_3} = \frac{{3280}}{{83}}\).
\({Q_1} = \frac{{136}}{5},{Q_3} = \frac{{3280}}{{83}}\).
\({Q_1} = \frac{{136}}{5},{Q_3} = \frac{{800}}{{21}}\).
Đo chiều cao (tính bằng cm) của \[500\] học sinh trong một trường THPT ta thu được kết quả như sau:
Chiều cao | \[\left[ {150;\,155} \right)\] | \[\left[ {155;\,160} \right)\] | \[\left[ {160;\,165} \right)\] | \[\left[ {165;\,170} \right)\] | \[\left[ {170;\,175} \right)\] | \[\left[ {175;\,180} \right)\] |
Số học sinh | 25 | 50 | 200 | 165 | 50 | 10 |
Tính mốt của mẫu số liệu ghép nhóm trên.
160.
164,05.
162,5.
160,94.
Trong hoạt động bảo vệ môi trường, các học sinh lớp 11A1 tiến hành trồng cây. Kết quả sau hoạt động được ghi lại ở bảng sau:
Số cây | \(\left[ {1;8} \right)\) | \(\left[ {8;15} \right)\) | \(\left[ {15;22} \right)\) | \(\left[ {22;29} \right)\) | \(\left[ {29;36} \right)\) |
Số học sinh | 7 | 15 | 6 | 10 | 3 |
Hãy tìm số trung vị của mẫu số liệu ghép nhóm trên.
14,3.
25,5.
18 .
26.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho mẫu số liệu ghép nhóm về thống kê chiều cao của 35 cây bạch đàn trong rừng, ta có bảng số liệu sau:
Khoảng chiều cao (m) | [6,5; 7,0) | [7,0; 7,5) | [7,5; 8,0) | [8,0; 8,5) |
Số cây | 6 | 15 | 11 | 3 |
a) Cỡ mẫu của mẫu số liệu là 35.
b) Nhóm chứa trung vị của mẫu số liệu là [7,5; 8,0).
c) Điểm trung bình của các học sinh là 7,9 (kết quả làm tròn đến hàng phần chục).
d) Mốt của mẫu số liệu là 7,35 (kết quả làm tròn đến hàng phần trăm).
Cho mẫu số liệu ghép nhóm về lương của nhân viên trong một công ty như sau
Lương (triệu đồng) | [9; 12) | [12; 15) | [15; 18) | [18; 21) | [21; 24) |
Số nhân viên | 6 | 12 | 4 | 2 | 1 |
a) Giá trị đại diện của nhóm [9; 12) là 10,5.
b) Trung bình lương các nhân viên là 16,5 triệu đồng.
c) Nhóm chứa trung vị là [15; 18).
d) Tứ phân vị thứ ba gần bằng 15,56.
Một bảng xếp hạng đã tính điểm chuẩn hóa cho chỉ số nghiên cứu của một số trường đại học ở Việt Nam và thu được kết quả sau:
Điểm | [10; 20) | [20; 30) | [30; 40) | [40; 50) | [50; 60) | [60;70) |
Số trường | 4 | 19 | 6 | 2 | 3 | 1 |
Khi đó:
a) Số liệu đã cho có 35 trường.
b) Số trung vị của mẫu số liệu là \({M_e} = 12\).
c) Số trung bình của mẫu số liệu đã cho là 28.
d) Ngưỡng điểm đề ra danh sách 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam là trên 35,42.
Phần III. Trắc nghiệm trả lời ngắn
Điểm thi giữa kì 1 môn Toán của một lớp học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Điểm thi | [1,5; 4,5) | [4,5; 7,5) | [7,5; 10,5) |
Số học sinh | 7 | 18 | 10 |
Tìm số trung vị của mẫu số liệu ghép nhóm trên.
Kết quả đo khối lượng của 30 củ khoai tây ở nông trường được biểu diễn ở biểu đồ dưới đây
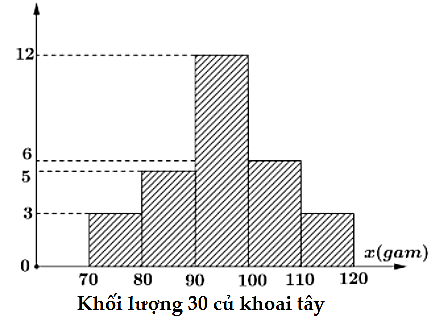
Tính gần đúng đến hàng phần chục mốt của mẫu số liệu trên.
Kết quả khảo sát độ cận thị mắt của 100 học sinh trường tiểu học X được cho như bảng
Độ cận | [0,25; 0,75) | [0,75; 1,25) | [1,25; 1,75) | [1,75; 2,25) | [2,25; 2,75) | [2,75; 3,25) |
Số học sinh | 25 | 38 | 21 | 12 | 3 | 1 |
Bác sĩ sẽ chọn ra 25% học sinh có độ cận cao nhất để tư vấn phụ huynh trong vấn đề chăm sóc đôi mắt, giảm khả năng tăng độ nhanh. Học sinh có độ cận từ bao nhiêu độ thì bác sĩ sẽ mời tư vấn phụ huynh? (làm tròn kết quả đến hàng phần trăm).
B. TỰ LUẬN
a) Cho \[\sin \alpha = \frac{2}{3}\], tính giá trị của biểu thức \[P = (1 - 3\cos \alpha )(1 + 3\cos \alpha )\].
b) Cho \(\sin \alpha = \frac{3}{5}\)và \({\rm{90}}^\circ < \alpha < 180^\circ \). Tính giá trị của biểu thức \(E = \frac{{\cot \alpha - 2\tan \alpha }}{{\tan \alpha + 3\cot \alpha }}\) .
Tìm tập xác định của các hàm số sau
a) \(y = \tan \left( {2x + \frac{\pi }{6}} \right)\) ; b) \(y = \cot \left( { - 2x - \frac{\pi }{3}} \right)\); c) \(y = \frac{2}{{\sin 2x}}\) .
Giải các phương trình sau
a) \(\sin \left( {3x - \frac{{3\pi }}{4}} \right) = \sin \left( {\frac{\pi }{6} - x} \right)\); b) \(\cos \left( {2x + 25^\circ } \right) = - \frac{{\sqrt 2 }}{2}\).
Giải các phương trình sau
a) \(\tan \left( {2x - 1} \right) = \tan \left( { - x + \frac{\pi }{3}} \right)\); b) \(\cot \left( {2x - \frac{\pi }{3}} \right) = 1\).
Giải các phương trình sau
a) \(\frac{3}{2} - 3\cos 4x = 6\sin x.\sin 3x\); b) \(\sin 4x + 1 - 2\cos 2x = \sin 2x\).
Tìm nghiệm lớn nhất của phương trình \(2\cos 2x - 1 = 0\) trong đoạn \(\left[ {0;\pi } \right]\).
Tìm m để phương trình \[2{\sin ^2}\frac{x}{2} + \sqrt 3 \sin x - 5m = 0\]luôn có nghiệm.
Xét tính tăng giảm của các dãy số sau:
a) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {3^n} - n.\) b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{n}{{{n^2} + 1}}\).
Chứng minh dãy số \(\left( {{u_n}} \right)\), với\({u_n} = \frac{{7n + 5}}{{5n + 7}}\) là một dãy số tăng và bị chặn.
Tìm số hạng đầu tiên, công sai, số hạng thứ \(20\) và tổng của \(20\) số hạng đầu tiên của các cấp số cộng sau, biết rằng:
a) \(\left\{ \begin{array}{l}{u_5} = 19\\{u_9} = 35\end{array} \right.\);
b) \(\left\{ \begin{array}{l}{u_3} + {u_5} = 14\\{s_{12}} = 129\end{array} \right.\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 4\). Tìm giá trị nhỏ nhất của \({u_1}{u_2} + {u_2}{u_3} + {u_3}{u_1}\)?
Cho cấp số nhân\(\left( {{u_n}} \right)\) có các số hạng thỏa mãn: \(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right.\)
a) Tìm số hạng đầu và công bội của cấp số nhân.
b)Hỏi tổng bao nhiêu số hạng đầu tiên bằng 3069?
c) Số 12288 là số hạng thứ mấy?
Tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu là \(\frac{1}{2}\), số hạng thứ tư là \(32\) và số hạng cuối là \(2048\)?
Một đa giác có chu vi là \[158\;{\rm{cm}}\], độ dài các cạnh của nó lập thành một cấp số cộng. Biết cạnh lớn nhất có độ dài là \[44\;{\rm{cm}}\]. Tìm số cạnh của đa giác đó?
Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt \(20000\) đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc trước. Người đó thua \(9\) lần liên tiếp và thắng ở lần thứ \(10.\) Hỏi du khác trên thắng hay thua bao nhiêu?
Cho bảng tần số ghép nhóm số liệu thống kê chiều cao của 40 mẫu cây ở một vườn thực vật (đơn vị: centimét).
Nhóm | Tần số |
\(\left[ {30;40} \right)\) | \(4\) |
\(\left[ {40;50} \right)\) | \(10\) |
\(\left[ {50;60} \right)\) | \(14\) |
\(\left[ {60;70} \right)\) | \(6\) |
\(\left[ {70;80} \right)\) | \(4\) |
\(\left[ {80;90} \right)\) | \(2\) |
| \(n = 40\) |
a) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
b) Mốt của mẫu số liệu trên là bao nhiêu?
Một câu lạc bộ thể dục thể thao đã ghi lại số giờ các thành viên của mình sử dụng cơ sở vậtchất của câu lạc bộ để tập luyện trong một tháng. Thu được mẫu số liệu ghép nhóm sau
Thời gian (giờ) | \(\left[ {1;5} \right)\) | \(\left[ {5;9} \right)\) | \(\left[ {9;13} \right)\) | \(\left[ {13;17} \right)\) | \(\left[ {17;21} \right)\) | \(\left[ {21;25} \right)\) |
Tần số (Số người) | 10 | 14 | 31 | 2 | 5 | 23 |
Hãy tính (làm tròn kết quả đến hàng phần mười)
a) Trung vị của mẫu số liệu.
b) Trung bình của mẫu số liệu. Trong trường hợp này thì trung bình hay trung vị đại diện tốt hơn cho mẫu số liệu?