Đề cương ôn tập giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Bài 2: Công thức lượng giác
16 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Trong các công thức dưới đây, công thức nào đúng?
\(\cos a - \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}.\)
\(\cos a - \cos b = 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}.\)
\(\cos a - \cos b = - 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}.\)
\(\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}.\)
Trong các công thức dưới đây, công thức nào đúng?
\(\cos \left( {a + b} \right) = \sin a.\cos b - \cos a.\sin b\).
\(\cos \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\).
\(\cos \left( {a + b} \right) = \cos a.\cos b + \sin a.\sin b\).
\(\cos \left( {a + b} \right) = \cos a.\cos b - \sin a.\sin b\).
Cho \[{\rm{cos}}\alpha \,\,{\rm{ = }}\,\,\frac{1}{3}\]. Tính \[{\rm{cos}}2\alpha \].
\[{\rm{cos}}2\alpha = \frac{7}{9}\].
\[{\rm{cos}}2\alpha = \frac{1}{3}\].
\[{\rm{cos}}2\alpha = - \frac{7}{9}\].
\[{\rm{cos}}2\alpha = \frac{2}{3}\].
Rút gọn biểu thức \[T = \sin \left( {\frac{\pi }{3} + x} \right) - \sin \left( {\frac{\pi }{3} - x} \right)\] ta được kết quả là
\[T = \sqrt 3 \cos x\].
\[T = \sin x\].
\[\frac{{\sqrt 3 }}{2}\].
\[T = \sin 2x\].
Cho \[\tan \alpha = 2\]. Tính \[\tan \left( {\alpha - \frac{\pi }{4}} \right)\].
\[ - \frac{1}{3}\].
\[1\].
\[\frac{2}{3}\].
\[\frac{1}{3}\].
Trong bốn khẳng định sau, có bao nhiêu khẳng định đúng?
(1): \(\cos 4a = {\cos ^2}2a - {\sin ^2}2a.\)
(2): \(\cos 4a = 1 - 2{\sin ^2}2a.\)
(3): \(\cos 4a = 2{\cos ^2}2a - 1.\)
(4): \(\cos 4a = 1 - 2{\sin ^2}4a.\)
\[4\].
\[3\].
\[2\].
\[1\].
Tính giá trị biểu thức \(P = \sin 30^\circ \cos 90^\circ + \sin 90^\circ \cos 30^\circ .\)
\[P = 1\].
\[P = 0\].
\[P = - \frac{{\sqrt 3 }}{2}\].
\[P = \frac{{\sqrt 3 }}{2}\].
Rút gọn biểu thức \(A = \frac{{\cos x + \cos 2x + \cos 3x}}{{\sin x + \sin 2x + \sin 3x}}\) ta được
\[A = \tan 2x\].
\[A = - \tan 2x\].
\[A = - \cot 2x\].
\[A = \cot 2x\].
Biết \(\frac{{\cos 4x + \cos 2x + 1}}{{\sin 4x + \sin 2x}} = m\cot 2x\). Khẳng định nào dưới đây là đúng.
\[m \in \left( {0;2} \right]\].
\[m \in \left( {0;1} \right)\].
\[m \in \left( {2;4} \right)\].
\[m \in \left( {1;2} \right]\].
Cho \(\sin \alpha = \frac{1}{3}\) và \(\frac{\pi }{2} < \alpha < \pi \). Biết giá trị của \(\cos \left( {\alpha - \frac{\pi }{6}} \right) = \frac{{1 - a\sqrt 6 }}{b}\) với \(a,b \in \mathbb{N}\). Tính \(a + b.\)
\[4\].
\[10\].
\[7\].
\[8\].
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Trong vật lí, phương trình tổng quát của một dao động điều hòa cho bởi công thức \(x\left( t \right) = A\cos \left( {\omega t + \varphi } \right)\), trong đó \(t\) là thời điểm (tính bằng giây), \(x\left( t \right)\) là li độ của vật tại thời điểm \(t\), \(A\) là biên độ dao động (\(A > 0\)) và \(\varphi \in \left[ { - \pi ;\pi } \right]\) là pha ban đầu của dao động. Xét hai dao động điều hòa có phương trình là \({x_1}\left( t \right) = 3\cos \left( {\frac{\pi }{4}t + \frac{{5\pi }}{6}} \right)\) cm; \({x_2}\left( t \right) = 3\cos \left( {\frac{\pi }{4}t + \frac{\pi }{3}} \right)\) cm.
a) Biên độ của dao động thứ nhất bằng 3 cm.
b) Pha ban đầu của dao động thứ hai bằng \( - \frac{\pi }{3}\).
c) Với \(a,b \in \mathbb{R}\) ta có \(\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\).
d) Biên độ và pha ban đầu của dao động tổng hợp \(x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right)\) lần lượt bằng \(3\sqrt 2 \)cm và \(\frac{{7\pi }}{{12}}\).
Cho \(\sin \alpha = \frac{2}{3}\) với \(0 < \alpha < \frac{\pi }{2}\).
a) \(\sin 2\alpha = \frac{{4\sqrt 5 }}{9}\).
b)\(\cos \left( {\alpha + \frac{{3\pi }}{2}} \right) = \frac{2}{3}\).
c) \(\sqrt 2 \cos \left( {\alpha + \frac{\pi }{4}} \right) = \frac{{2 + \sqrt 5 }}{3}\).
d) \(D = \frac{{\cot \alpha + \tan \alpha }}{{\cot \alpha - \tan \alpha }} = \frac{1}{9}\).
Cho \(\cos 2\alpha = - \frac{1}{9},\alpha \in \left( { - \frac{\pi }{2};0} \right)\).
a)\({\sin ^2}\alpha = \frac{{1 + \sin 2\alpha }}{2}\).
b)\(\cos \alpha = \frac{2}{3}\).
c) \(\sin 4\alpha = \frac{{80}}{{81}}\).
d) Biết \(\tan \left( {\alpha + \frac{\pi }{4}} \right) = a + b\sqrt c ,\left( {a,b,c \in \mathbb{Z},c \ge 0} \right)\). Khi đó \(a + b + c = 0\).
Phần III. Trắc nghiệm trả lời ngắn
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m.
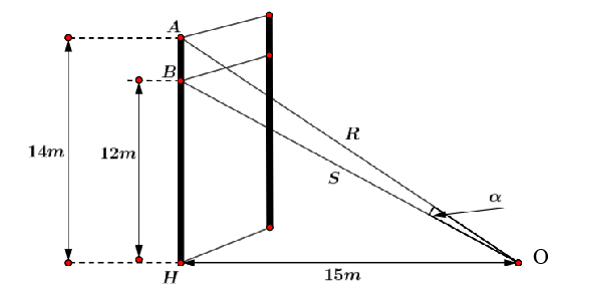
Với α là góc giữa hai sợi cáp trên thỏa mãn \(\tan \alpha = \frac{a}{b}\left( {a,b \in \mathbb{N}} \right)\); \(\frac{a}{b}\) là phân số tối giản. Tính a + b.
Cho tam giác \(ABC\) có \(\cos A = \frac{4}{5}\) và \(\cos B = \frac{5}{{13}}\). Tính giá trị của biểu thức \(A = 130\cos C - 1\).
Tính giá trị của biểu thức \(A = \cos \left( {\frac{\pi }{3} - x} \right)\cos \left( {\frac{\pi }{4} + x} \right) + \cos \left( {\frac{\pi }{6} + x} \right)\cos \left( {\frac{{3\pi }}{4} + x} \right)\) ta được \(A = \cos \frac{a}{b}\pi \) với \(\frac{a}{b}\) là phân số tối giản, \(a,b \in \mathbb{Z}\). Tính \(\frac{a}{b}\) (kết quả làm tròn đến hàng phần trăm).