10 câu hỏi
Xét các khẳng định sau :
A: “Qua ba điểm xác định một mặt phẳng”.
B: “Qua một điểm và một đường thẳng xác định một mặt phẳng”.
C: “Qua hai đường thẳng xác định một mặt phẳng”.
D: “Qua ba đường thẳng a, b, c phân biệt đồng qui tại một điểm thì xác định một mặt phẳng”.
Chọn khẳng định đúng :
A, B đúng; C, D sai.
A, B, C đúng; D sai.
A đúng; B, C, D sai.
A, B, C, D sai.
Các khẳng định dưới đây, khẳng định nào đúng?
Qua 2 điểm phân biệt có duy nhất một mặt phẳng\[.\]
Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng\[.\]
Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng\[.\]
Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng\[.\]
Một hình tứ diện có số mặt và số cạnh là
4 mặt, 6 cạnh.
\[5\] mặt, \[10\] cạnh.
\[5\] mặt, \[5\] cạnh.
\[6\] mặt, 4 cạnh.
Trong các mệnh đề sau mệnh đề nào sai?
Dùng nét đứt biểu diễn cho đường bị che khuất.
Hình biểu diễn của đường thẳng là đường thẳng.
Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng..
Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song.
Cho hình chóp \(S.ABCD\) (đáy là một tứ giác lồi). Gọi \(\left( P \right)\) là mặt phẳng bất kì cắt hình chóp. Khi đó, thiết diện do mặt phẳng \(\left( P \right)\) cắt hình chóp là một đa giác có số cạnh tối đa là bao nhiêu?
\(3\).
\(4\).
\(5\).
\(6\).
Cho tứ diện \(ABCD\). \(G\) là trọng tâm của tam giác \(BCD\). Giao tuyến của mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\) là:
\(AM\) (\(M\) là trung điểm của \(AB\)).
\(AN\) (\(N\) là trung điểm của \(CD\)).
\(AH\) (\(H\) là hình chiếu của \(B\) trên \(CD\)).
\(AK\) (\(K\) là hình chiếu của \(C\) trên \(BD\)).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(SB\). Khẳng định nào sau đây là sai?
\(IJCD\) là hình thang.
\(\left( {SAB} \right) \cap \left( {IBC} \right) = IB\).
\(\left( {SBD} \right) \cap \left( {JCD} \right) = JD\).
\(\left( {IAC} \right) \cap \left( {JBD} \right) = AO\) (\(O\) là tâm \(ABCD\)).
Cho hình chóp \(S.ABCD\)có đáy là hình bình hành. Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(AB,AD,SC\). Khi đó giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\)và \(\left( {SBC} \right)\)là đường thẳng \(d\)có đặc điểm gì?
Đường thẳng \[d\] đi qua điểm \(P\).
Đường thẳng \[d\] trùng với đường thẳng\(PM\).
Đường thẳng \[d\] trùng với đường thẳng\(PN\).
Đường thẳng \[d\] đi qua điểm \(P\)và giao điểm của \(BC\) với \(MN\).
Cho hình chóp \(S.ABCD\) có \(AC \cap BD = O\) và \(AD \cap BC = I.\)
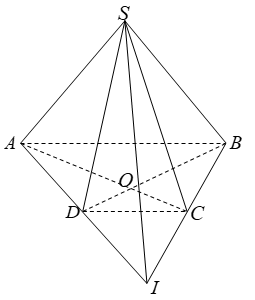
Giao tuyến của mặt phẳng \(\left( {SAD} \right)\) và mặt phẳng \(\left( {SBC} \right)\) là đường thẳng:
\(SI\)
\(SA.\)
\(OI.\)
\(SO.\)
Cho hình chóp \(S.ABCD\), O là giao điểm của \(AC\) và \(BD\). Trên \(SC\) lấy điểm \(M\)không trùng với \(S,C\). Tìm giao điểm của \(SD\) và \(\left( {ABM} \right)\)?
Giao điểm của \(SD\) và \(AB\).
Giao điểm của \(SD\) và \(AM\).
Giao điểm của \(SD\) và \(BK\) với \(K = AM \cap SO\).
Giao điểm của \(SD\) và \(MK\) với \(K = AM \cap SO\).
