Đề cương ôn tập giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Bài 5. Tích của một số với một vectơ
11 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho số \(k \ne 0\) và \(\overrightarrow a \ne \overrightarrow 0 \). Tìm khẳng định sai trong các khẳng định sau.
\[0.\overrightarrow a = \overrightarrow 0 \].
\[ - k.\overrightarrow 0 = \overrightarrow 0 \].
\[0.\overrightarrow a = 0\].
\[k.\overrightarrow 0 = \overrightarrow 0 \].
Cho đoạn thẳng \[AB\]và điểm I thỏa mãn \[\overrightarrow {IB} + 3\overrightarrow {IA} = \overrightarrow 0 \]. Hình nào sau đây mô tả đúng giả thiết này?
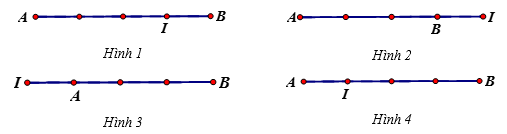
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho tam giác \[ABC\] có \[G\] là trọng tâm và \[I\] là trung điểm của \[BC.\] Đẳng thức nào sau đây đúng ?
\[\overrightarrow {GA} = 2\,\overrightarrow {GI} .\]
\[\overrightarrow {IG} = - \frac{1}{3}\overrightarrow {IA} .\]
\[\overrightarrow {GB} + \overrightarrow {GC} = 2\,\overrightarrow {GI} .\]
\[\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} .\]
Cho tam giác \[ABC\] có \[M\] là trung điểm của \[BC,\,\,\,I\] là trung điểm của \[AM.\] Khẳng định nào sau đây đúng ?
\[\overrightarrow {IB} + 2\overrightarrow {IC} + \overrightarrow {IA} = \overrightarrow 0 .\]
\[\overrightarrow {IB} + \overrightarrow {IC} + 2\overrightarrow {IA} = \overrightarrow 0 .\]
\[2\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {IA} = \overrightarrow 0 .\]
\[\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {IA} = \overrightarrow 0 .\]
Cho tam giác \(ABC\), có bao nhiêu điểm \(M\) thỏa \[\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 5\]?
\(1\).
\(2\).
vô số.
Không có điểm nào.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho tam giác ABC có trọng tâm G, gọi M là trung điểm BC. B' là điểm đối xứng của B qua G.
a) Tứ giác AGCB' là hình bình hành.
b) \(\overrightarrow {CB'} = - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
c) \(\overrightarrow {AB'} = - \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \).
d) \(\overrightarrow {MB'} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Cho DABC. Gọi M, N lần lượt là trung điểm của AB, AC.
a) \(2\overrightarrow {CM} = \overrightarrow {CB} + \overrightarrow {CA} \).
b) \(\overrightarrow {AB} = - \frac{2}{3}\overrightarrow {CM} - \frac{4}{3}\overrightarrow {BN} \).
c) \(\overrightarrow {AC} = \frac{4}{3}\overrightarrow {CM} + \frac{2}{3}\overrightarrow {BN} \).
d) \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {BN} - \frac{1}{3}\overrightarrow {CM} \).
Cho DABC có trọng tâm G. Gọi M là trung điểm BC.
a) \(\overrightarrow {BC} = 2\overrightarrow {BM} \).
b) \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AM} \).
c) \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} \).
d) \(\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
Phần III. Trắc nghiệm trả lời ngắn
Cho tam giác ABC. Tia đối của tia CB lấy điểm D sao cho \(CD = \frac{1}{2}CB\). Gọi \(x,y\) là các số thực thỏa mãn \(\overrightarrow {AD} = x\overrightarrow {AB} + y\overrightarrow {AC} \). Tính giá trị của \(\left| {xy} \right|\).
Cho tam giác ABC, gọi D là điểm trên cạnh BC sao cho \(\overrightarrow {BD} = \frac{2}{3}\overrightarrow {BC} \) và I là trung điểm của AD. Gọi M là điểm thỏa mãn \(\overrightarrow {AM} = \frac{2}{5}\overrightarrow {AC} \). Biết rằng \(\overrightarrow {BI} = k\overrightarrow {BM} \). Tính giá trị của \(T = 6k\).
Cho tam giác vuông ABC có AB = 1, AC = 2. Điểm N thỏa mãn \(\overrightarrow {CN} = \overrightarrow {CA} + \overrightarrow {CB} + \overrightarrow {CI} \) với I là trung điểm AB. Tính độ dài vectơ \(\overrightarrow {CN} \) (kết quả làm tròn đến hàng phần trăm).



