CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN

Biết rằng hàm số \({\rm{y}} = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{x}} - 1}}\) có đồ thị như Hình 2. Giá trị của \({\rm{a}} + {\rm{b}}\) là bao nhiêu?

Biết rằng hàm số $\mathrm{y}=\mathrm{a}\mathrm{x}+\mathrm{b}+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{d}}(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\in \mathbb{R})$ có đồ thị như Hình 3.

Giá trị của $\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}$ là bao nhiêu?

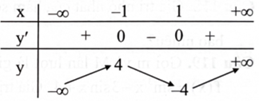
Cho hàm số \({\rm{y}} = {\rm{a}}{{\rm{x}}^3} + {\rm{b}}{{\rm{x}}^2} + {\rm{cx}} + {\rm{d}}\)\(({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R})\) có bảng biến thiên như hình bên. Giá trị của \({\rm{a}} + {\rm{b}} + {\rm{c}} + {\rm{d}}\) là bao nhiêu?

Cho hàm số \(y = \frac{{ax + 2}}{{x + b}}(a,b \in \mathbb{R})\) có bảng biến thiên như hình bên. Giá trị của \({\rm{a}} + {\rm{b}}\) là bao nhiêu?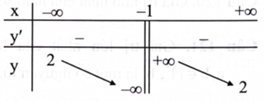 

Hệ số góc của tiếp tuyến của đồ thị hàm số \({\rm{y}} = {{\rm{x}}^3} - {\rm{x}} - 1\) tại điểm có hoành độ bằng 3 bằng bao nhiêu?

Phương trình tiếp tuyến của đồ thị hàm số \({\rm{y}} = \frac{{\rm{x}}}{{{\rm{x}} - 1}}\) tại điểm có hoành độ bằng 2 là \({\rm{y}} = {\rm{ax}} + {\rm{b}}\) với \({\rm{a}},{\rm{b}} \in \mathbb{R}.\) Giá trị của biểu thức \({\rm{S}} = 4{\rm{a}} - 5\;{\rm{b}}\) là bao nhiêu?

Cho hàm số \(y = f(x)\) có \({f^\prime }(x) = {x^2} - 3x - 4.\) Tập nghiệm của bất phương trình \({{\rm{f}}^\prime }({\rm{x}}) < 0\) là \(({\rm{a}};{\rm{b}})\) với \({\rm{a}},{\rm{b}} \in \mathbb{R}.\) Giá trị của biểu thức \({\rm{A}} = {\rm{b}} - {\rm{a}}\) là bao nhiêu?

Cho hàm số \(y = f(x)\) có \({f^\prime }(x) = \frac{{ - {x^2} + 10x - 24}}{{{{(x - 5)}^2}}}.\) Tập nghiệm của bất phương trình \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\) là \([{\rm{a}};{\rm{c}}) \cup ({\rm{c}};{\rm{b}}]\) với \({\rm{a}},{\rm{b}},{\rm{c}} \in \mathbb{R}.\) Giá trị của biểu thức \({\rm{B}} = {\rm{a}} + 2\;{\rm{b}} + 3{\rm{c}}\) là bao nhiêu?

Cho đồ thị hàm số \({\rm{y}} = \frac{{3{\rm{x}} + 2}}{{{\rm{x}} - 4}}\) có đường tiệm cận đứng \({\rm{x}} = {\rm{a}}\) và đường tiệm cận ngang \({\rm{y}} = {\rm{b}}\) với \({\rm{a}},{\rm{b}} \in \mathbb{R}.\) Giá trị của biểu thức \({\rm{C}} = 5{\rm{a}} + 6\;{\rm{b}}\) là bao nhiêu?

Cho đồ thị hàm số \({\rm{y}} = \frac{{{{\rm{x}}^2}}}{{{\rm{x}} - 3}}\) có đường tiệm cận xiên \({\rm{y}} = {\rm{ax}} + {\rm{b}}\) với \({\rm{a}},{\rm{b}} \in \mathbb{R}.\) Giá trị của biểu thức \({\rm{D}} = {\rm{a}} - {{\rm{b}}^2}\) là bao nhiêu?

Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) thoả mãn \({{\rm{f}}^\prime }({\rm{x}}) = ({\rm{x}} - 1){({\rm{x}} - 2)^2}({\rm{x}} - 3).\) Tổng các điểm cực trị của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) là bao nhiêu?

Giá trị nhỏ nhất của hàm số \({\rm{f}}({\rm{x}}) = {\rm{x}} + \frac{1}{{\rm{x}}}\) trên nửa khoảng \([5; + \infty )\) bằng bao nhiêu?

Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f(x) = {\sin ^3}x - 3\sin x + 4.\) Giá trị của \(2m + 3M\) là bao nhiêu?

Giá trị nhỏ nhất của hàm số \(P = {\log ^2}x + \frac{1}{{{{\log }^2}x + 2}}\) bằng bao nhiêu?

Giá trị lớn nhất của hàm số \({\rm{f}}({\rm{x}}) = {\rm{x}} + \sqrt {4 - {{\rm{x}}^2}} \) bằng \({\rm{a}}\sqrt {\rm{b}} \) với \({\rm{a}},{\rm{b}} \in {\mathbb{N}^*},\;{\rm{b}}\) là một số nguyên tố. Giá trị của \({\rm{a}} + {\rm{b}}\) là bao nhiêu?

Giá trị lớn nhất của hàm số \({\rm{f}}({\rm{x}}) = 2\sin {\rm{x}} - \frac{4}{3}{\sin ^3}{\rm{x}}\) trên \([0;\pi ]\) bằng \(\frac{{\rm{a}}}{{\rm{b}}}\sqrt {\rm{c}} \) với \({\rm{a}},{\rm{b}},{\rm{c}} \in {\mathbb{N}^*},\;{\rm{b}} < 6,{\rm{c}}\) là một số nguyên tố. Giá trị của \({\rm{a}} + {\rm{b}} + {\rm{c}}\) là bao nhiêu?

Biết rằng đồ thị hàm số \({\rm{f}}({\rm{x}}) = {\rm{x}} + \frac{1}{{\rm{x}}}\) có một tâm đối xứng là \({\rm{I}}({\rm{a}};{\rm{b}}).\) Giá trị của \({\rm{a}} + {\rm{b}}\) là bao nhiêu?

Biết rằng đồ thị hàm số \({\rm{f}}({\rm{x}}) = {{\rm{x}}^4} - {{\rm{x}}^2}\) có một trục đối xứng là đường thẳng \({\rm{x}} = {\rm{a}}.\) Giá trị của a là bao nhiêu?

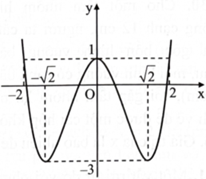
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Biết rằng hàm số đồng biến trên \(( - \sqrt 2 ;{\rm{a}})\) và nghịch biến trên \(({\rm{a}};\sqrt 2 ).\)Giá trị của a là bao nhiêu?

Một sợi dây kim loại được treo giữa hai bức tường. Độ cao so với mặt đất của chiếc dây này được cho bởi hàm số:

\(h(x) = {e^{ - 2x}} + {e^x},0 \le x \le 2\)

trong đó  là khoảng cách dọc theo mặt đất từ bức tường bên trái. Hỏi sợi dây sẽ gần với mặt đất một khoảng ngắn nhất là bao nhiêu mét? (Làm tròn kết quả đến hàng phần trăm)

Một nhà sản xuất áo sơ mi bán \(x\) chiếc mỗi ngày với hàm số biểu thị doanh thu: \({\rm{R}}({\rm{x}}) = 200\ln \left( {1 + \frac{{\rm{x}}}{{100}}} \right) + 1000\) (đô la). Chi phí sản xuất được xác định bởi hàm: \({\rm{C}}({\rm{x}}) = {({\rm{x}} - 100)^2} + 200\) (đô la). Lợi nhuận tối đa mỗi ngày của nhà sản xuất là bao nhiêu? (Làm tròn kết quả đến hàng đơn vị)

Một nhà sản xuất ấm điện thực hiện một nghiên cứu kiểm soát chi phí và phát hiện ra rằng để sản xuất \(x\) ấm đun nước mỗi ngày, chi phí cho mỗi ấm \({\rm{C}}({\rm{x}})\) được xác định bởi công thức: \({\rm{C}}({\rm{x}}) = 4\ln {\rm{x}} + {\left( {\frac{{30 - {\rm{x}}}}{{10}}} \right)^2}\) (trăm đô la) với công suất sản xuất tối thiểu 10 ấm/ngày. Cần sản xuất bao nhiêu ấm đun nước để giữ giá thành mỗi ấm ở mức tối thiểu?

Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật có đáy là hình vuông sao cho thể tích khối hộp được tạo thành là \(8{\rm{d}}{{\rm{m}}^3}\) và diện tích toàn phần đạt giá trị nhỏ nhất. Độ dài cạnh đáy của mỗi hộp muốn thiết kế là bao nhiêu decimét?

Cho một tấm nhôm hình vuông cạnh 12 cm, người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x(\;{\rm{cm}})\), rồi gập tấm nhôm lại như hình vẽ để được một cái hộp không nắp. Giá trị của \(x\) là bao nhiêu để hộp nhận được có thể tích lớn nhất?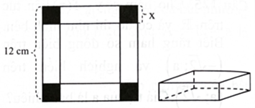 

Một vật rơi tự do với phương trình chuyển động \({\rm{S}} = \frac{1}{2}{\rm{g}}{{\rm{t}}^2}\), trong đó t tính bằng giây \(({\rm{s}})\) và \({\rm{g}} = 9,8\;{\rm{m}}/{{\rm{s}}^2}.\) Vận tốc của vật tại thời điểm \({\rm{t}} = 5\;{\rm{s}}\) là bai nhiêu \({\rm{m}}/{\rm{s}}\) ?

Một chất điểm chuyển động thẳng theo phương trình \({\rm{S}} = {{\rm{t}}^3} - 3{{\rm{t}}^2} + 4{\rm{t}}\), trong đó t tính bằng giây \(({\rm{s}})\) và S tính bằng mét \(({\rm{m}}).\) Thời điểm vận tốc của chất điểm đạt giá trị \(4\;{\rm{m}}/{\rm{s}}\) là bao nhiêu giây?

Một chất điểm chuyển động theo phương trình \({\rm{S}} =  - {{\rm{t}}^3} + 9{{\rm{t}}^2} + {\rm{t}} + 10\), trong đó t tính bằng giây \(({\rm{s}})\) và S tính bằng mét \(({\rm{m}}).\) Thời điểm t mà tại đó vận tốc \(({\rm{m}}/{\rm{s}})\) của chất điểm đạt giá trị lớn nhất là bao nhiêu giây?

Một chất điểm chuyển động theo quy luật \(S = 6{{\rm{t}}^2} - {{\rm{t}}^3}\) (trong đó t là khoảng thời gian tính bằng giây ( s ) từ lúc chất điểm bắt đầu chuyển động). Thời điểm t mà tại đó vận tốc \(({\rm{m}}/{\rm{s}})\) của chất điểm đạt giá trị lớn nhất là bao nhiêu giây?

Một vật chuyển động theo quy luật \(s = \frac{{ - {t^3}}}{2} + 9{{\rm{t}}^2}\), với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 12 giây, kể từ lúc vật bắt đầu chuyển động, tại thời điểm \(t\) bằng bao nhiêu giây thì vận tốc của vật đạt giá trị lớn nhất?

Cho chuyển động thẳng xác định bởi phương trình \({\rm{S}} = {{\rm{t}}^3} + 3{{\rm{t}}^2} - 9{\rm{t}} + 27\), trong đó t tính bằng giây \(({\rm{s}})\) và S tính bằng mét \(({\rm{m}}).\) Gia tốc của chuyển động tại thời điểm vận tốc triệt tiêu là bao nhiêu \({\rm{m}}/{{\rm{s}}^2}\) ?

Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \({\rm{f}}({\rm{t}}) = 45{{\rm{t}}^2} - {{\rm{t}}^3}\) (kết quả khảo sát được trong 8 tháng gần đây). Nếu xem \({{\rm{f}}^\prime }({\rm{t}})\) là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\) thì tốc độ truyền bệnh lớn nhất vào ngày thứ bao nhiêu?

Một vật chuyển động theo quy luật \(s = \frac{{ - 1}}{3}{t^3} + 9{t^2}\), với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(s\) (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đẩu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu \({\rm{m}}/{\rm{s}}\) ?

Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là \(V = 250\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\), các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ đó bằng \({\rm{V}} = 250\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\) và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu centimét?

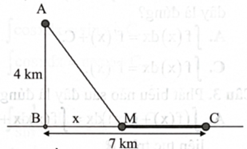
Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng \({\rm{AB}} = 4\;{\rm{km}}.\) Trên bờ biển có một cái kho ở vị trí C cách B một khoảng \({\rm{BC}} = 7\;{\rm{km}}.\) Người canh hải đăng chèo đò từ vị trí A đến vị trí M trên bờ biển với vận tốc \(6\;{\rm{km}}/{\rm{h}}\) rồi đi xe đạp từ M đến C

với vận tốc \(10\;{\rm{km}}/{\rm{h}}.\) Người đó nên chèo thuyền trong bao nhiêu ki-lô-mét nếu anh ta muốn đến nơi trong thời gian ngắn nhất?