CÂU TRẮC NGHIỆM ĐÚNG SAI

b) \({f^\prime }(1) = 2.\)

c) \(f(1) = 0.\)

d) Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ \({{\rm{x}}_0} = 1\) là \({\rm{y}} = 2{\rm{x}} - 2.\)

a) \({f^\prime }(x) =  - {x^2} + 1.\)

b) \({{\rm{f}}^\prime }({\rm{x}}) > 0 \Leftrightarrow {\rm{x}} \in ( - 1;1),{{\rm{f}}^\prime }({\rm{x}}) < 0 \Leftrightarrow {\rm{x}} \in ( - \infty ; - 1) \cup (1; + \infty ).\)

c) \({\rm{f}}(1) = 12,{\rm{f}}( - 1) = 8.\)

d) Hàm số đạt giá trị nhỏ nhất bằng 8 tại \({x_1} =  - 1\), đạt giá trị lớn nhất bằng 12 tại \({{\rm{x}}_2} = 1.\)

a) \({f^\prime }(x) = a{x^2} + bx + c.\)

b) Nếu biểu thức \({\Delta ^\prime } = {{\rm{b}}^2} - 3{\rm{ac}}\) nhận giá trị dương thì phương trình \({{\rm{f}}^\prime }({\rm{x}}) = 0\) có hai nghiệm \({x_1},{x_2}\) phân biệt.

c) Nếu phương trình \({{\rm{f}}^\prime }({\rm{x}}) = 0\) có hai nghiệm \({{\rm{x}}_1},{{\rm{x}}_2}\) phân biệt \(\left( {{{\rm{x}}_1} < {{\rm{x}}_2}} \right)\) thì hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có bảng biến thiên là

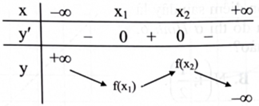
d) Nếu phương trình \({{\rm{f}}^\prime }({\rm{x}}) = 0\) có hai nghiệm \({{\rm{x}}_1},{{\rm{x}}_2}\) phân biệt \(\left( {{{\rm{x}}_1} < {{\rm{x}}_2}} \right)\) thì \({{\rm{x}}_1}\) là điểm cực tiểu, \({{\rm{x}}_2}\) là điểm cực đại của hàm số.

a) \({f^\prime }(x) = 6{x^2} - 6x.\)

b) Phương trình \({{\rm{f}}^\prime }({\rm{x}}) = 0\) có hai nghiệm phân biệt là 0 và 1.

c) Hàm số đã cho có bảng biến thiên như sau

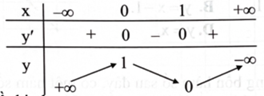
d) Hàm số đã cho có đồ thị như sau

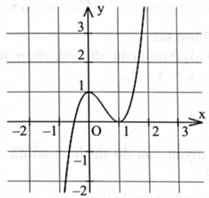
a) \({f^\prime }(x) = 1 - \frac{1}{{{{(x - 1)}^2}}}.\)

b) Phương trình \({{\rm{f}}^\prime }({\rm{x}}) = 0\) có hai nghiệm phân biệt là 0 và 2.

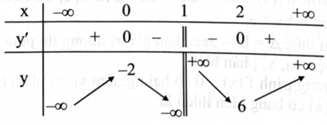
c) Hàm số đã cho có bảng biến thiên như sau

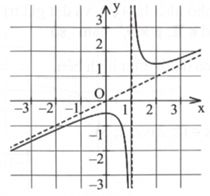
d) Hàm số đã cho có đồ thị như sau

a) \(f(x) = \frac{3}{{{{(2x - 1)}^2}}}.\)

b) \({{\rm{f}}^\prime }({\rm{x}})\) nhận giá trị dương với mọi \(x\) thuộc tập xác định.

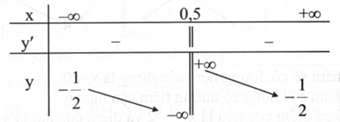
c) Hàm số đã cho có bảng biến thiên như sau

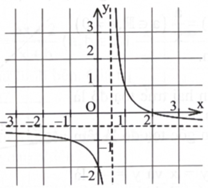
d) Hàm số đã cho có đồ thị như sau

a) Tập xác định của hàm số là [0; 32].

b)\({f^\prime }(x) = \frac{1}{{2\sqrt x }} - \frac{1}{{2\sqrt {32 - x} }}.\)

c) Phương trình \({{\rm{f}}^\prime }({\rm{x}}) = 0\) có hai nghiệm phân biệt.

d) Hàm số đạt giá trị nhỏ nhất là \(4\sqrt 2 \) và đạt giá trị lớn nhất là 8.

a) \({\rm{d}} =  - 2.\)

b) \({\rm{a}} - \frac{{\rm{c}}}{{{{({\rm{x}} + {\rm{d}})}^2}}} > 0\quad \forall {\rm{x}} \in (1;2) \cup (2;3).\)

c) \({\rm{a}} = 1,\;{\rm{b}} = - 1.\)

d) \({\rm{c}} =  - 2.\)

a) Đồ thị hàm số có đường tiệm cận đứng là \(x = 0.\)

b) Đồ thị hàm số không có đường tiệm cận ngang.

c) Hàm số có điểm cực tiểu là \({x_1} =  - 2\) và điểm cực đại là \({x_2} = 2.\)

d) Hàm số có giá trị cực tiểu là 4 và giá trị cực đại là -4.

a) \({\rm{a}} = - 4.\)

b) Đồ thị hàm số nhận hai trục tọa độ là hai đường tiệm cận.

c) Đồ thị hàm số nhận gốc toạ độ là tâm đối xứng

d) Các đường thẳng \({\rm{y}} = {\rm{x}}\) và \({\rm{y}} =  - {\rm{x}}\) là các trục đối xứng của đồ thị hàm số.