12 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Với \(a\) là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
\({a^{\frac{5}{2}}}\).
\(a\).
\({a^{\frac{3}{2}}}\).
\({a^{\frac{1}{4}}}\).
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
\(\frac{5}{{2a}}\).
\(\frac{{5a}}{2}\).
\(\frac{2}{{5a}}\).
\(\frac{{2a}}{5}\).
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{e}} \right)^x}\).
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\).
\(y = {\left( {\frac{1}{3}} \right)^x}\).
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\).
Tập nghiệm \(S\) của bất phương trình \(\log x < 1\) là
\(S = \left( { - \infty ;10} \right)\).
\(S = \left( {0;10} \right)\).
\(S = \left( {10; + \infty } \right)\).
\(S = \left( { - \infty ;1} \right)\).
Cho \({\log _a}b = 2\) với \(a,b\) là số thực dương và \(a\) khác 1. Tính giá trị biểu thức \(T = {\log _{{a^2}}}{b^6} + {\log _a}\sqrt b \).
\(T = 7\).
\(T = 6\).
\(T = 5\).
\(T = 8\).
Trong hình vẽ bên có đồ thị các hàm số \(y = {a^x},y = {b^x},y = {\log _c}x\). Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
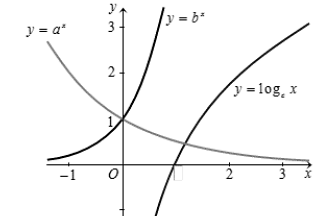
\(a < c < b\).
\(c < a < b\).
\(a < b = c\).
\(b < c < a\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Góc giữa hai đường thẳng \(SD\) và \(BC\) bằng
Góc giữa hai đường thẳng \(SD\) và \(DC\).
Góc giữa hai đường thẳng \(SD\) và \(AD\).
Góc giữa hai đường thẳng \(SD\) và \(BD\).
Góc giữa hai đường thẳng \(SD\) và \(SC\).
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình vuông tâm \(O\). Hình chiếu của điểm \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là điểm
\(B\).
\(D\).
\(O\).
\(A\).
Cho các đường thẳng \(a,b\) và các mặt phẳng \(\left( \alpha \right),\left( \beta \right)\). Chọn mệnh đề đúng trong các mệnh đề sau
\(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\a \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
\(\left\{ \begin{array}{l}a \bot b\\a \bot \left( \alpha \right)\end{array} \right. \Rightarrow b//\left( \alpha \right)\).
\(\left\{ \begin{array}{l}a \bot b\\a \subset \left( \alpha \right)\\b \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
\(\left\{ \begin{array}{l}\left( \alpha \right) \bot \left( \beta \right)\\a \subset \left( \alpha \right)\\b \subset \left( \beta \right)\end{array} \right. \Rightarrow a \bot b\).
Một khối lăng trụ có diện tích đáy bằng 3 và thể tích bằng 6 thì chiều cao bằng
\(6\).
\(4\).
\(2\).
\(3\).
Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\), chiều cao bằng \(\frac{a}{2}\). Gọi \(M\) là trung điểm \(CD\) như hình vẽ. Tính số đo góc phẳng nhị diện \(\left[ {S,CD,O} \right]\).
![Cho hình chóp tứ giác đều có cạnh đáy bằng a , chiều cao bằng a 2 . Gọi M là trung điểm C D như hình vẽ. Tính số đo góc phẳng nhị diện [ S , C D , O ] . (ảnh 1)](https://video.vietjack.com/upload2/images/1736661471/1736662222-image3.png)
\(45^\circ \).
\(90^\circ \).
\(30^\circ \).
\(60^\circ \).
Cho tứ diện \[ABCD\] có \[AD \bot (ABC)\], \[AC = AD = 2\], \[AB = 1\] và \[BC = \sqrt 5 \]. Tính khoảng cách \[d\] từ \[A\] đến mặt phẳng \[\left( {BCD} \right)\].
\[d = \frac{{\sqrt 6 }}{3}\].
\[d = \frac{{\sqrt 6 }}{2}\].
\[d = \frac{{2\sqrt 5 }}{5}\].
\[d = \frac{{\sqrt 2 }}{2}\].
