12 CÂU HỎI
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{2}{{x - 1}}\;{\rm{khi}}\;x \ge 2\\{x^2} + 1\;{\rm{khi}}\;x < 2\end{array} \right.\). Khi đó, \(f\left( 2 \right) + f\left( { - 2} \right)\) bằng
A. 7.
B. \(4\).
C. \(\frac{8}{3}\).
D. \( - 1\).
Cho hàm số \(y = - 3{x^2} - 4x + 3\) có đồ thị \(\left( P \right)\). Trục đối xứng của \(\left( P \right)\) là đường thẳng có phương trình là
A. \(x = \frac{2}{3}\).
B. \(x = - \frac{2}{3}\).
C. \(x = \frac{4}{3}\).
D. \(x = - \frac{4}{3}\).
Cho tam thức \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta < 0\). Tìm tất cả các giá trị của \(a\) để \(f\left( x \right) > 0,\forall x \in \mathbb{R}\).
A. \(a \le 0\).
B. \(a < 0\).
C. \(a > 0\).
D. \(a \ge 0\).
Nghiệm của phương trình \(\sqrt {2x - 1} = \sqrt {3 - x} \) là
A. \(x = \frac{3}{4}\).
B. \(x = \frac{2}{3}\).
C. \(x = \frac{4}{3}\).
D. \(x = \frac{3}{2}\).
Trong mặt phẳng \(Oxy\), cho hai điểm \(A\left( {1;3} \right),B\left( {2;7} \right)\). Một vectơ chỉ phương của đường thẳng \(AB\) là:
A. \(\overrightarrow {{u_1}} = \left( { - 4;1} \right)\).
B. \(\overrightarrow {{u_2}} = \left( { - 2;1} \right)\).
C. \(\overrightarrow {{u_3}} = \left( { - 3;2} \right)\).
D. \(\overrightarrow {{u_4}} = \left( {1;4} \right)\).
Trong mặt phẳng \(Oxy\), cho điểm \(M\left( {{x_0};{y_0}} \right)\) và đường thẳng \(\Delta :ax + by + c = 0\). Khoảng cách từ điểm \(M\) đến \(\Delta \) được tính bằng công thức:
A. \(d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0}} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
B. \(d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
C. \(d\left( {M,\Delta } \right) = \frac{{a{x_0} + b{y_0}}}{{\sqrt {{a^2} + {b^2}} }}\).
D. \(d\left( {M,\Delta } \right) = \frac{{a{x_0} + b{y_0} + c}}{{\sqrt {{a^2} + {b^2}} }}\).
Trong mặt phẳng \(Oxy\), bán kính của đường tròn \(\left( C \right):{x^2} + {y^2} - 10x - 11 = 0\) là
A. \(R = 36\).
B. \(R = 6\).
C. \(R = 14\).
D. \(R = \sqrt {14} \).
Cho elip \(\left( E \right)\) có phương trình chính tắc là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\). Gọi \(2c\) là tiêu cự của \(\left( E \right)\). Mệnh đề nào sau đây là đúng?
A. \({c^2} = 12\).
B. \({c^2} = 16\).
C. \({c^2} = 20\).
D. \({c^2} = 4\).
Cho hàm số bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có đồ thị là parabol như hình vẽ. Giá trị nhỏ nhất của hàm số trên tập số thực là
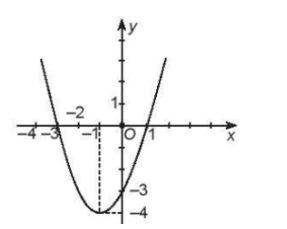
A.\( - 4\).
B. \(1\).
C. \( - 3\).
D. \( - 1\).
Tập nghiệm của bất phương trình \({x^2} - 3x + 2 < 0\) là
A. \(\left( {1;2} \right)\).
B. \(\left( {2; + \infty } \right)\).
C. \(\left( { - \infty ;1} \right) \cup \left( {2; + \infty } \right)\).
D. \(\left( { - \infty ;1} \right)\).
Trong mặt phẳng \(Oxy\), tìm cosin góc giữa hai đường thẳng \({d_1}:x + 2y - 7 = 0\), \({d_2}:2x - 4y + 9 = 0\).
A. \(\frac{3}{5}\).
B. \(\frac{2}{{\sqrt 5 }}\).
C. \(\frac{1}{5}\).
D. \( - \frac{3}{5}\).
Trong mặt phẳng \(Oxy\), tọa độ giao điểm của hai đường thẳng \({d_1}:2x + 3y - 19 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = 22 + 2t\\y = 55 + 5t\end{array} \right.\) là
A. \(\left( {5;2} \right)\).
B. \(\left( { - 1;7} \right)\).
C. \(\left( {2;5} \right)\).
D. \(\left( {10;25} \right)\).
Gợi ý cho bạn
Đề luyện thi số 03
Đề luyện thi số 03
Đề ôn luyện số 2
Đề luyện thi số 01
Toán 12 trung văn Quiz 1