Bộ 3 đề KSCL đầu năm Toán 9 có đáp án - Đề 2
18 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn
(Thí sinh trả lời từ Câu 1 đến Câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án)
Biểuthức\(\left( {2x - 1} \right)\left( {2x + 1} \right)\) viết gọn thành
\(2{x^2} - 1.\)
\({\left( {4x - 1} \right)^2}.\)
\(4{x^2} - 1.\)
\({\left( {2x - 1} \right)^2}.\)
Kếtquảphépnhân\(\frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{3x}} \cdot \frac{{6x}}{{{{\left( {x - 3} \right)}^2}}}\) là
\(\frac{2}{{x - 3}}.\)
\(\frac{{2\left( {x + 3} \right)}}{{x - 3}}.\)
\(\frac{2}{{x + 3}}.\)
\(\frac{2}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.\)
Sốnàosauđâylànghiệmcủaphươngtrình\[ - 5x + 10 = 0?\]
2.
1.
\[ - 1.\]
5.
Mộthộpcó4tấmthẻcùngloạiđượcđánhsốlầnlượt:\[2\,;\,\,3\,;\,\,4\,;\,\,5.\]Chọnngẫunhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ lớn hơn 3” là
Thẻghisố2vàthẻghisố3.
Thẻghisố2vàthẻ ghisố5.
Thẻghisố4vàthẻghisố5.
Thẻghisố3vàthẻghisố4.
Điểmnàosauđâythuộcđồthịhàmsố\[y = 2x - 5?\]
\[\left( {4\,;\,\,3} \right).\]
\[\left( {3\,;\,\, - 1} \right).\]
\[\left( { - 4\,;\,\, - 3} \right).\]
\[\left( {2\,;\,\,1} \right).\]
Hàmsốnàosauđâylàhàmsốbậcnhất?
\[y = \frac{1}{{2x}}.\]
\[y = \frac{1}{2}x - 1.\]
\[y = - 2{x^2} + 1.\]
\[y = \frac{1}{x} + 1.\]
Chotamgiác \[ABC,\,\,M\]và\[N\]thứtựlàtrungđiểmcủa \[AB,\,\,AC.\]Biết\[MN = 8\,\,{\rm{cm}},\]độ dài cạnh \[BC\] là
4cm.
8cm.
16cm.
32cm
Chohìnhvẽ,biết\[DE\,{\rm{//}}\,BC,\]độdài\[EC\](làmtrònđếnchữsốthậpphân thứ hai)là
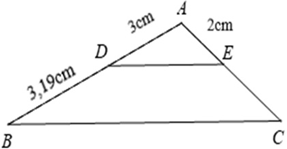
\[2,13\,\,{\rm{cm}}.\]
\[2,15\,\,{\rm{cm}}.\]
\[2,12\,\,{\rm{cm}}.\]
\[2,14\,\,{\rm{cm}}.\]
Phântíchđathức\[5x\left( {x-y} \right) - \left( {y - x} \right)\]thànhnhântửtađược
\[\left( {x-y} \right)(5x + 1).\]
\[5x\left( {x-y} \right).\]
\[\left( {x-y} \right)(5x-1).\]
\[\left( {x{\rm{ }} + y} \right)(5x-1).\]
Đườngthẳng\[y = 2x + 1\]vàđườngthẳng\[y = ax + m\]cắt nhaukhi
\[a = 2.\]
\[a \ne 2.\]
\[m \ne 1.\]
\[m = 1.\]
Hình chóp tam giác đều có diện tích đáy bằng \[15\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\] và chiều cao bằng 8 cm thì thể tích của hình chóp đều đó bằng
\[60\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\]
\[40\,\,{\rm{c}}{{\rm{m}}^2}.\]
\[120\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}{\rm{.}}\]
\[40\,\,{\rm{c}}{{\rm{m}}^3}.\]
Hìnhchóptứgiácđềucóbaonhiêumặt?
3.
2.
1.
5.
Phần II. Tự luận (7,0 điểm)
Cho biểu thức\(A = \left( {\frac{1}{{x + 1}} + \frac{1}{{{x^2} - 1}}} \right) \cdot \frac{{x - 1}}{x},\) với \(x \ne 0,\,\,x \ne 1,\,\,x \ne - 1.\)
1) Giải các phương trình sau:
a) \[3x - 5 = - 17.\] b) \(\frac{{3x + 2}}{2} - \frac{{3x + 1}}{6} = 2x + \frac{5}{3}.\)
2) Trong mặt phẳng tọa độ \[Oxy,\] vẽ đồ thị hàm số\[y = x + 2.\]
Một hộp quà trung thu có dạng hình chóp tứ giác đềucó độ dài cạnh đáy là \[6\,\,{\rm{cm}},\] độ dài trung đoạn là \[5\,\,{\rm{cm}}.\] Tính diện tích xung quanh của hộp quà đó. |  |
Một ô tô đi từ A đến B với vận tốc trung bình 50 km/h. Lúc từ B về A ô tô đi vớivận tốc nhỏ hơn vận tốc lúc đi 20 km/h nên thời gian về nhiều hơn thời gian đi là 40 phút. Tính quãng đường từ A đến B.
Cho \[\Delta ABC\]nhọn \[\left( {AB < AC} \right),\] ba đường cao \[AE,\,\,BD,\,\,CF\] cắt nhau tại \[H.\]
a) Chứng minh:
b) Chứng minh: \[AB \cdot DF = AD \cdot BC.\]
c) Chứng minh: \[BH \cdot BD + CH \cdot CF = B{C^2}\] và \(\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}} = 1.\)
Tìm giá trị nhỏ nhất của biểu thức: \[D = 2{x^2} + {y^2} - 6x + 2xy - 2y + 7.\]


