Bộ 3 đề KSCL đầu năm Toán 9 có đáp án - Đề 1
22 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn
(Thí sinh trả lời từ Câu 1 đến Câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án)
Biểu thức nào sau đây không phải là phân thức đại số?
\(\frac{{3x}}{y}.\)
\(\frac{{x - 2}}{0}.\)
\(\frac{1}{2}x + 1.\)
\(\frac{3}{{x + 4}}.\)
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
\[0x + 3 = 0.\]
\[{x^2} - 2 = 0.\]
\(\frac{1}{2}x - 3 = 0.\)
\(\frac{5}{x} + 1 = 0.\)
Đồ thị của hai hàm số \(y = 2025x + 1\) và \(y = 2026x + 1\) là hai đường thẳng có vị trí như thế nào?
Trùng nhau.
Song song.
Không cắt nhau.
Cắt nhau.
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\[2{x^2} + \;2 = \;0.\]
\[3y - 1 = \;5\left( {y - \;2} \right).\]
\(2x + \frac{y}{2} = 1.\)
\(3\sqrt x + {y^2} = 0.\)
Cho hình chóp tứ giác đều \[S.ABCD\] (hình bên), \[SH\] được gọi là
![Cho hình chóp tứ giác đều \[S.ABCD\] (hình bên), \[SH\] được gọi là (ảnh 1)](https://video.vietjack.com/upload2/images/1755653258/1755653342-image1.png)
đường cao.
cạnh bên.
cạnh đáy.
đường chéo
Cho \(\Delta ABC\) vuông tại \(A\) có \(AC = 4\,\,{\rm{cm}},\,\,AB = 3\,\,\,{\rm{cm}}.\) Khi đó \[\tan B\] bằng
\(\frac{3}{4}\).
\(\frac{3}{5}\).
\(\frac{4}{5}\).
\(\frac{4}{3}\).
Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 2” là
Thẻ ghi số 2 và thẻ ghi số 3.
Thẻ ghi số 2 và thẻ ghi số 4.
Thẻ ghi số 2 và thẻ ghi số 5.
Thẻ ghi số 3 và thẻ ghi số 4.
Cho tam giác \[ABC\] đồng dạng với tam giác \[MNP\] theo tỉ số 2. Khẳng định nào sau đây là đúng?
\[MN = 2AB.\]
\[AC = 2NP.\]
\[MP = 2BC.\]
\[BC = 2NP.\]
Cặp số \[\left( { - 2\,;\,\, - 3} \right)\] là nghiệm của hệ phương trình nào sau đây?
\[\left\{ \begin{array}{l}x - 2y = 3\\2x + y = 4\end{array} \right..\]
\[\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 8\end{array} \right..\]
\[\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 7\end{array} \right..\]
\[\left\{ \begin{array}{l}4x - 2y = 0\\x - 3y = 5\end{array} \right..\]
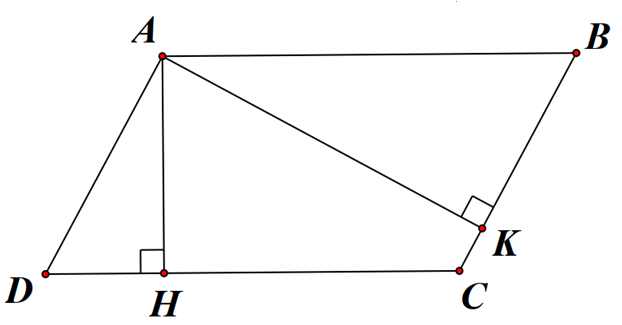
Cho hình bình hành \[ABCD,\] kẻ \[AH \bot CD\] tại \[H,\] \[AK \bot BC\] tại \[K.\] Khẳng định nào sau đây là đúng?
Bạn An gieo một con xúc xắc 50 lần và thống kê lại kết quả các lần gieo ở bảng sau:
Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần xuất hiện | 8 | 9 | 9 | 5 | 6 | 13 |
Xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ” sau 50 lần thử trên là
\[0,46.\]
\[0,52.\]
\[0,54.\]
\[0,48.\]
Cho \[\Delta ABC\] vuông tại \[A,\] đường cao \[AH\] có \[AC = 15\,\,{\rm{cm}},\,\,CH = 6\,\,{\rm{cm}}.\] Tỉ số lượng giác \(\cos B\) bằng
\[\frac{5}{{\sqrt {21} }}.\]
\[\frac{{\sqrt {21} }}{5}.\]
\[\frac{5}{2}.\]
\[\frac{2}{5}.\]
Phần II. Câu trắc nghiệm đúng sai
(Thí sinh trả lời từ Câu 13 đến Câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Cho biểu thức \[P = \frac{{{x^2} - 6x + 9}}{{9 - {x^2}}} + \frac{{4x + 8}}{{x + 3}}.\]
a) Điều kiện xác định của biểu thức \[P\]là \[x \ne 3.\]
b) Rút gọn \[P = \frac{{3x + 11}}{{x + 3}}.\]
c) Giá trị của P tại \[x = - 2\]là 5.
d) \[x \in \left\{ { - 2\,;\,\, - 1\,;\,\, - 4} \right\}\]thì biểu thức \[P\]nhận giá trị nguyên.
Một hộp có 25 thẻ cùng loại, mỗi thẻ được ghi một trong các số \[1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\, \ldots \,;\,\,25\,;\]hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Gọi \[A\]là biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5” và \[B\]là biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5”.
a) Có 3 kết quả thuận lợi cho biến cố \[A\].
b) Có 2 kết quả thuận lợi cho biến cố \[B\].
c) \[P\left( A \right) = \frac{1}{5}.\]
d) \[P\left( B \right) = \frac{2}{{25}}.\]
Cho phương trình \[x + 2y = 3.\]
a) Phương trình đã cho là phương trình bậc nhất một ẩn.
b) Cặp số \[\left( {5\,;\,\, - 1} \right)\]là một nghiệm của phương trình đã cho.
c) Tất cả nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng \(y = 3 - \frac{1}{2}x.\)
d) Phương trình đã cho có vô số nghiệm, nghiệm tổng quát là \[\left( {3 - 2y\,;\,\,y} \right)\]với \[y \in \mathbb{R}\] tùy ý.
Cho tam giác \[ABC\]cân tại \[A\]có \[AB = 2a\]và \[\widehat B = \;\alpha .\] Kẻ đường trung tuyến \[AM.\] Khi đó:
a) \[\sin \widehat {BAM} = \cos \alpha .\]
b) \[BM = 2a \cdot \sin a.\]
c) \[AM = 2a \cdot \cos \alpha .\]
d) Diện tích tam giác \[ABC\]là: \[S = 4{a^2} \cdot \sin \alpha \cdot \cos \alpha .\]
PHẦNIII.Câutrắcnghiệmtrảlờingắn(ThísinhtrảlờitừCâu17đếnCâu22)
Cho hệ phương trình \(\left\{ \begin{array}{l}ax + 6y = 5\\5x + by = 4\end{array} \right.\)nhận cặp số \[\left( {2\,;\,\, - 1} \right)\] làm nghiệm. Tính tổng bình phương của \[a\]và \[b\](làm tròn đến hàng phần mười).
Camera quan sát tại đường X trong 365 ngày liên tiếp ghi nhận 217 bị tắc đường vào giờ cao điểm buổi sáng (từ 7 giờ 30 phút đến 8 giờ). Từ số liệu thống kê đó, hãy dự đoán xem trong 100 ngày có khoảng bao nhiêu ngày bị tắc đường vào giờ cao điểm buổi sáng tại đường X?
Mộtkhốirubikcódạnghìnhchóptamgiácđềuvớidiệntíchđáylà \[22,45\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\]vàthểtíchcủakhốiđólà\[44,002\,\,{\rm{c}}{{\rm{m}}^3}.\]Tínhchiều cao của khốirubikđó.(đơnvị: cm) |  |
Mộtngườiđixemáytừ\[A\]đến\[B\]vớivậntốc40km/h.Lúcvềngườiđótăngvận tốcthêm5 km/h,biếtthờigianlúcvềíthơnthờigianlúcđilà20phút.Tínhquãngđường \[AB.\](đơnvị: km)
Tạihaiđiểm\[A,\,\,B\]cáchnhau \[500{\rm{ m}},\]người tanhìnthấyđỉnhnúivớigócnânglầnlượtlà\[34^\circ \]và\[38^\circ .\]Tínhchiềucaocủangọnnúi. (đơnvị:m; kếtquảlàmtrònđếnhàngđơnvị)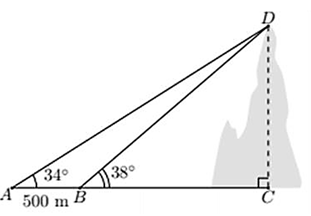
Tại\({a^3} + {b^3} + {c^3} = 3abc\) và \(a + b + c \ne 0.\)Tínhgiátrịcủabiểuthức \(N = \frac{{{a^2} + {b^2} + {c^2}}}{{{{\left( {a + b + c} \right)}^2}}}.\)(kếtquảlàmtrònđếnhàngphần trăm)


