12 câu hỏi
Biểu thức nào sau đây không phải là biểu thức đại số?
\(5xy.\)
\[4x-2{y^3}.\]
\(\frac{{3x}}{0}.\)
\(5 \cdot \frac{1}{2} - 7.\)
Biểu thức nào sau đây là đa thức một biến?
\[x + 7xy.\]
\({x^5}-5y.\)
\[{x^2} + 9.\]
\(\frac{1}{x} + 13x - 5.\)
Tổng của hai đa thức \({y^2} + 2y\) và \(4y - {y^2}\) là
\(2{y^2} - 6y.\)
\(6y{\rm{.}}\)
\( - 2y{\rm{.}}\)
\(2y{\rm{.}}\)
Kết quả của phép tính \[3{x^2}:\;x\] là
\(3x.\)B. \(3{x^3}.\)C. \(x.\)D. \[3.\]
Cho tam giác \[ABC\] có số đo \(\widehat A,\,\,\widehat B,\,\,\widehat C\) theo thứ tự là \[80^\circ ;{\rm{ }}60^\circ ;{\rm{ }}40^\circ .\] Khẳng định nào sau đây là đúng?
\(BC > AC > AB.\)
\(BC < AC < AB.\)
</>
\[BC > AB > AC.\]
\(AB < BC < AC.\)
</>
Cho ba điểm \[A,{\rm{ }}B,{\rm{ }}C\] thẳng hàng và \[B\] nằm giữa \[A\] và \[C.\] Trên đường thẳng vuông góc với \[AC\] tại \[B\] ta lấy điểm \[H.\] Khi đó
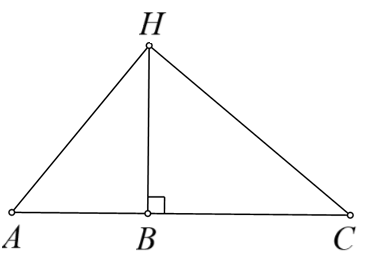
\(AH < BH.\)
</>
\(AH < AB.\)
</>
\[AH > BH.\]
\(AH = BH.\)
Gieo ngẫu nhiên xúc xắc một lần, kết quả có thể xảy ra đối với mặt xuất hiện là mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 4 chấm, mặt 5 chấm, mặt 6 chấm. Xét biến cố A: “Mặt xuất hiện của xúc xắc có số chấm là số lẻ” thì xác suất của biến cố này là
\(\frac{1}{3}\).
\(\frac{1}{6}\).
\(\frac{2}{3}\).
\(\frac{1}{2}\).
Tam giác \[ABC\] có độ dài cạnh đáy là \[a\,\,({\rm{cm}})\] và chiều cao tương ứng là \[h\,\,({\rm{cm}}).\] Biểu thức đại số tính diện tích tam giác \[ABC\] là
\[\frac{{a + h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
\[\frac{{a \cdot h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
\[a + h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
\[a \cdot h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Kết quả của phép tính \(2{x^2} \cdot \left( {3x + {x^2} - 5{x^3}} \right)\,\) là
\(6{x^3}\, + 2{x^4}\, - 10{x^5}.\)
\(5{x^3}\, + 2{x^4}\, - 10{x^5}.\)
\(6{x^3}\, + 2{x^4}\, - 10{x^6}.\)
\(6{x^3}\, - 2{x^4}\, - 10{x^5}.\)
Cho \(\Delta ABC\) có các đường trung tuyến \(AN\) và \(BM\) cắt nhau tại \(G\). Phát biểu nào sau là sai?
\(G\) là trọng tâm của \(\Delta ABC\).
\(CG\) đi qua trung điểm của \(AB\).
\(\frac{{GM}}{{AM}} = \frac{2}{3}\).
\[BG = 2GN\].
Hiệu của hai đa thức \[{x^2}--2x + 1\] và \[ - 2{x^2}--2x - 1\] là
\[3{x^2} + 2.\]
\[{x^2}.\]
\[3{x^2} - 2.\]
\[{x^2} - 2.\]
Bạn Nam xuất phát từ điểm \[M\] bên hồ bơi. Bạn ấy muốn bơi theo đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Nam phải bơi theo đường nào?
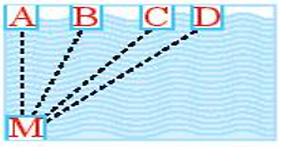
\[MA.\]
\[MB.\]
\[MC.\]
\[MD.\]
