12 câu hỏi
Trên tia số, cho hai điểm \[A\] và \[B\] lần lượt biểu diễn số 6 và 10. Gọi \[M\] là tập hợp các số tự nhiên biểu diễn thuộc đoạn \[AB,\] khi đó \[M\] là tập hợp nào dưới đây?
\(M = \left\{ {7;\,\,8;\,\,9} \right\}.\)
\(M = \left\{ {6;\,\,7;\,\,8;\,\,9} \right\}.\)
\(M = \left\{ {7;\,\,8;\,\,9;\,\,10} \right\}.\)
\(M = \left\{ {6;\,\,7;\,\,8;\,\,9;\,\,10} \right\}.\)
Với hai số tự nhiên \(m,\,\,n\) thì
\({a^m} + {a^n} = {a^{m\,\, \cdot \,\,n}}.\)
\({a^m} - {a^n} = {a^{m\,\,:\,\,n}}.\)
\({a^m} \cdot {a^n} = {a^{m\, + \,n}}.\)
\({a^m}:{a^n} = {a^{m\,\,\,:\,\,\,n}}.\)
Tập hợp nào sau đây có các phần tử đều là số nguyên tố?
\(\left\{ {1;\,\,3;\,\,5;\,\,7} \right\}.\)
\(\left\{ {13;\,\,15;\,\,17;\,\,29} \right\}.\)
\(\left\{ {3;\,\,5;\,\,7;\,\,51} \right\}.\)
\(\left\{ {5;\,\,11;\,\,17;\,\,23} \right\}.\)
Trong các khẳng định sau, khẳng định nào là đúng?
BCNN của \(a\) và \(b\) là số nhỏ nhất trong tập hợp bội chung của \(a\) và \(b.\)
BCNN\(\left( {a,\,\,b,\,\,1} \right) = \)BCNN\(\left( {a,\,\,b} \right).\)
Nếu \(m\,\, \vdots \,\,n\) thì BCNN\(\left( {m,\,\,n} \right) = n.\)
Nếu ƯCLN\(\left( {x,\,\,y} \right) = 1\) thì BCNN\(\left( {x,\,\,y} \right) = 1.\)
Cách viết nào sau đây là đúng?
\( - 6 \in \mathbb{N}.\)
\( - 9 \notin \mathbb{Z}.\)
\( - 9 \in \mathbb{N}.\)
\( - 1 \in \mathbb{Z}.\)
Một chiếc tàu ngầm đang ở độ cao \( - 20\) m so với mực nước biển. Tàu tiếp tục lặn sâu xuống thêm 30 m. Khi đó, độ cao của tàu ngầm so với mực nước biển là
10 m.
\( - 10\) m.
50 m.
\( - 50\) m.
Tổng tất cả các số nguyên \(x\) mà \( - 4 \le x < 6\) là
0.
1.
5.
\( - 10.\)
Cho lục giác đều \(ABCDEG\) có tâm \(O.\) Có bao nhiêu đoạn thẳng bằng với đoạn thẳng \(OA?\)
6.
8.
9.
11.
Cho hình thang \(ABCD\) như hình vẽ bên. Diện tích của hình thang \(ABCD\) là
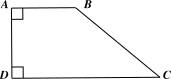
\(\left( {AB + CD} \right) \cdot AD.\)
\(\frac{{\left( {AB + CD} \right) \cdot AD}}{2}.\)
\(2\left( {AB + CD} \right) \cdot AD.\)
\(\frac{{AB \cdot CD \cdot AD}}{2}.\)
Cho các chữ cái sau đây:

Có bao nhiêu chữ cái có trục đối xứng?
5.
6.
7.
8.
Khẳng định nào sau đây là sai?
Hình tròn vừa có trục đối xứng vừa có tâm đối xứng.
Hình vuông có tâm đối xứng là giao điểm của hai đường chéo.
Hình chữ nhật vừa có trục đối xứng vừa có tâm đối xứng.
Hình bình hành vừa có trục đối xứng vừa có tâm đối xứng.
Khẳng định nào sau đây là đúng?
Tính đối xứng chỉ thể hiện trong Toán học.
Tính đối xứng không thể hiện trong Sinh học.
Tính đối xứng không thể hiện trong Kiến trúc.
Tính đối xứng thể hiện trong Toán học, Tự nhiên, Kiến trúc, Nghệ thuật, Công nghệ chế tạo, ...
