Bài tập ôn tập Toán 9 Chân trời sáng tạo Chương 1 có đáp án
60 câu hỏi
A. Trắc nghiệm
Dạng 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Điều kiện xác định của phương trình \(\frac{{4x - 1}}{{x + 2}} + 1 = \frac{3}{{x - 3}}\) là
\(x \ne - 2\).
\(x \ne 3\).
\(x \ne - 2\) và \(x \ne 3\).
\(x = - 2\) và \(x = 3\).
Trong các phương trình sau, phương trình nào là phương trình tích?
\(\left( {2x + 1} \right)\left( {x - 2} \right) = 1\).
\(x\left( {x - 2} \right) + \left( {6x + 5} \right)\left( {x + 1} \right) = 0\).
\(x - 5 = - 2x + 3\).
\(\left( {x + 4} \right)\left( {5 - 2x} \right) = 0\).
Mẫu thức chung đơn giản nhất khi quy đồng mẫu thức hai vế của phương trình \(\frac{{x + 3}}{{x - 3}} + \frac{{2x - 1}}{{3 - x}} = 5\) là
\({\left( {x - 3} \right)^2}\).
\(\left( {x - 3} \right)\left( {3 - x} \right)\).
\(x - 3\).
\(5\left( {x - 3} \right)\).
Phương trình \[\frac{{x + 6}}{{x + 5}} + \frac{3}{2} = 2\] có nghiệm là
\[x = - 7.\]
\[x = 7.\]
\[x = - \frac{7}{3}.\]
\[x = - \frac{3}{7}.\]
Giá trị của \[m\] để phương trình \[\left( {2m - 5} \right)x - 2{m^2} + 8 = 43\] có nghiệm \(x = - 7\) là
\[m = 0\] hoặc \[m = 7\].
\[m = 1\] hoặc \[m = - 7\].
\[m = 0\] hoặc \[m = - 7\].
\[m = - 7\].
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\[2{x^2} + 2 = 0\].
\[3y - 1 = 5\left( {y - 2} \right)\].
\[2x + \frac{y}{2} - 1 = 0\].
\[3\sqrt x + {y^2} = 0\].
Hệ số \(a,\,\,b\) và \(c\) tương ứng của phương trình bậc nhất hai ẩn \( - 2x = 13\) là
\(a = - 2\,;\,\,b = 0\) và \(c = 13\).
\(a = - 2\,;\,\,b = 13\) và \(c = 0\).
\(a = 0\,;\,\,b = - 2\) và \(c = 13\).
\(a = 13\,;\,\,b = 0\) và \(c = - 2\).
Trong các hệ thức sau, hệ thức nào không phải là phương trình bậc nhất hai ẩn?
\(x - 2y = 3\).
\(0x - 0y = 5\).
\(0x + 3y = 1\).
\( - 3x + 0y = 3\).
Phương trình nào dưới đây nhận cặp số \(\left( { - 2\,;\,\,4} \right)\) làm nghiệm?
\[x - 2y = 0\].
\[2x + y = 0\].
\[x - y = 2\].
\[x + 2y + 1 = 0\].
Cặp số nào không là nghiệm của phương trình \(x + 2y = - 3\)?
\(\left( {1\,;\,\, - 2} \right)\).
\(\left( { - 2\,;\,\, - 0,5} \right)\).
\(\left( {3\,;\,\,3} \right)\).
\(\left( { - 5\,;\,\,1} \right)\).
Cặp số \[\left( { - 2;\,\,3} \right)\] là nghiệm của phương trình nào dưới đây?
\(x - y = 1\).
\(2x - y = - 7\).
\(2x + y = 2\).
\(x - 3y = - 10\).
Cho phương trình \[ax + by = c\] với \[a \ne 0\,,\,\,b \ne 0\]. Nghiệm của phương trình được biểu diễn bởi
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\y = - \frac{a}{b}x + \frac{c}{b}\end{array} \right.\].
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\y = - \frac{a}{b}x - \frac{c}{b}\end{array} \right.\].
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{c}{b}\end{array} \right.\].
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\y = - \frac{c}{b}\end{array} \right.\].
Công thức nghiệm tổng quát của phương trình \[0x + 4y = - 16\] là
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\y = - 4\end{array} \right.\].
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 4\end{array} \right.\].
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\x = - 4\end{array} \right.\].
\[\left\{ \begin{array}{l}x \in \mathbb{R}\\x = 4\end{array} \right.\].
Tập nghiệm của phương trình \(5x + 0y = 2\) được biểu diễn bởi
đường thẳng \(y = 5x + 2\).
đường thẳng \(y = \frac{2}{5}\).
đường thẳng \(x = \frac{2}{5}\).
đường thẳng \(y = 2 - 5x\).
Tập nghiệm của phương trình \[4x--3y = - 1\] được biểu diễn bằng đường thẳng nào dưới đây?
\(y = - 4x - 1\)
\(y = \frac{4}{3}x + \frac{1}{3}\).
\(y = 4x + 1\).
\(y = \frac{4}{3}x - \frac{1}{3}\).
Giá trị nào của \({x_0}\) để cặp số \(\left( {{x_0}\,;\,\, - 1} \right)\) là nghiệm của phương trình \(3x + y = 2\)?
\({x_0} = - 1.\)
\({x_0} = 1.\)
\({x_0} = 2.\)
\({x_0} = 3.\)
Giá trị nào của \({y_0}\) để cặp số \(\left( {0,5\,;\,\,{y_0}} \right)\) là nghiệm của phương trình \( - 2x + 2y = 3\)?
\({y_0} = - 1\).
\({y_0} = - 2\).
\({y_0} = 2.\)
\({y_0} = 3\).
Giá trị dương của \(m\) để phương trình \[2x - {(m - 2)^2}y = 5\] nhận cặp số \(\left( { - 10\,;\,\, - 1} \right)\) làm nghiệm là
\[m = 5\].
\[m = 7\].
\[m = - 3\].
\[m = 7\,;\,\,m = - 3\].
Cho đường thẳng \(d\) có phương trình \[\left( {2m - 4} \right)x + \left( {m - 1} \right)y = m - 5\]. Giá trị của tham số \(m\) để đường thẳng \(d\) đi qua gốc tọa độ là
\[m = 2\].
\[m = 1\].
\[m = 5\].
\[m \ne 5\].
Phương trình có nghiệm \(\left( {1\,;\,\,2} \right)\) khi \(m\) có giá trị là
\(m = 3\).
\(m = 1\).
\(m = 5\)
\(m = 0\).
Cho đường thẳng \(d\) có phương trình \(\left( {m - 2} \right)x + \left( {3m - 1} \right)y = 6m - 2\). Giá trị của tham số \[m\] để \[d\] song song với trục hoành là
\[m = 1\].
\[m = 2\].
\[m = 3\].
\[m = 4\].
Cho đường thẳng \(d\) có phương trình \(\left( {m - 2} \right)x + \left( {3m - 1} \right)y = 6m - 2\). Giá trị của tham số \[m\] để \(d\) song song với trục tung là
\[m = \frac{1}{3}\].
\[m = \frac{2}{3}\].
\[m \ne 2\].
\[m \ne \frac{1}{3}\].
Cho đường thẳng nào đưới đây có biểu diễn hình học là đường thẳng song song với trục hoành?
\[5y = 7\].
\[3x = 9\].
\[x + y = 9\].
\[6y + x = 7\].
Các phương trình sau, phương trình nào có nghiệm nguyên?
\(2x - 4y = 7\)
\(3x + 6y = 19\)
\(5x - 10y = 14\)
\(3x + 12y = 6\)
Tìm tất cả nghiệm nguyên của phương trình \[5x - 3y = 8\].
\[\left\{ \begin{array}{l}x = 3t - 8\\y = 5t - 16\end{array} \right.\,\,(t \in \mathbb{Z})\].
\[\left\{ \begin{array}{l}x = 3t - 8\\y = - 5t - 6\end{array} \right.\,\,(t \in \mathbb{Z})\].
\[\left\{ \begin{array}{l}x = 8t - 3\\y = 15t - 16\end{array} \right.\,\,(t \in \mathbb{Z})\].
\[\left\{ \begin{array}{l}x = 3t + 8\\y = 5t + 6\end{array} \right.\,\,(t \in \mathbb{Z})\].
Nghiệm nguyên âm lớn nhất của phương trình \[ - 5x + 2y = 7\] là
\[( - 7\,;\,\, - 14)\].
\[( - 1\,;\,\, - 2)\].
\[( - 3\,;\,\, - 4)\].
\[( - 5\,;\,\, - 9)\].
Nghiệm nguyên âm của phương trình \[3x + 4y = - 10\] là \[(x\,;\,\,y)\]. Tính \(x \cdot y\).
\[2\].
\( - 2\).
\(6\).
\(4\).
Biết hệ phương trình nhận cặp số là một nghiệm. Khi đó, g\[\left\{ \begin{array}{l}ax - 3y = 1\\x + by = - 5\end{array} \right.\]iá trị của \(a,\,\,b\) là
\[a = 4;\] \[b = \frac{7}{3}\].
\[a = - 4;\] \[b = \frac{7}{3}\].
\[a = 4;\] \[b = - \frac{7}{3}\].
\[a = - 4;\] \[b = - \frac{7}{3}\].
Một lạng (0,1 kg) thịt bò chứa \(26\,\,{\rm{g}}\) protein, một lạng (0,1 kg) cá chứa \(22\,\,{\rm{g}}\) protein. Bác An định chỉ bổ sung \(70\,\,{\rm{g}}\) protein từ thịt bò và thịt cá trong một ngày. Gọi \(x,\,\,y\) lần lượt là số lạng thịt bò, số lạng thịt cá mà bác An ăn trong một ngày. Phương trình bậc nhất hai ẩn \(x,\,\,y\) biểu diễn nhu cầu bổ sung protein của bác An là
\(x + 22y = 70\).
\(70x - 22y = 26\).
\(22x + 26y = 70\).
\(26x + 22y = 70\).
Cho \(\left( {x;\,\,y} \right)\) là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}\frac{3}{x} + \frac{2}{y} = 7\\\frac{2}{x} - \frac{5}{y} = - 27\end{array} \right.\] và cùng với các khẳng định sau:
(i) Hệ phương trình cho điều kiện xác định là \(x \ne 0\) và \(y \ne 0.\)
(ii) Hệ phương trình có nghiệm là \(\left( { - 1;\,\,5} \right)\).\(\frac{{19}}{y} = 95,\)
(iii) Tổng bình phương của \(x\) và \(y\) lớn hơn 20.\[\left\{ \begin{array}{l}\frac{6}{x} + \frac{4}{y} = 14\\\frac{6}{x} - \frac{{15}}{y} = - 81.\end{array} \right.\]
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
0.
1.
2.
3.
Để chuẩn bị cho buổi liên hoan của gia đình, bác Ngọc mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là \(130\) nghìn đồng/kg, giá tiền cá chép là \(50\) nghìn đồng/kg. Bác Ngọc đã chi \(295\) nghìn để mua \(3,5\,\,{\rm{kg}}\) hai loại thực phẩm trên. Gọi \(x\) và \(y\) lần lượt là số kilogam thịt lợn và cá chép mà bác Ngọc đã mua. Hệ phương trình bậc nhất hai ẩn \(x\) và \(y\) là
\(\left\{ \begin{array}{l}x + y = 3,5\\130x + 50y = 295\end{array} \right.\).
\(\left\{ \begin{array}{l}x - y = 3,5\\130x + y = 295\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y = 3,5\\x + 50y = 295\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y = 295\\130x + 50y = 3,5\end{array} \right.\)
Đường thẳng \({d_1}:y = \frac{1}{2}x\) và \({d_2}:y = - x + 3\) cắt nhau tại điểm \(M\). Tọa điểm \(M\) là cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 0\\x + y = 3\end{array} \right.\)?
\(M\left( {1\,;\,\,2} \right)\).
\(M\left( {2\,;\,\,0} \right)\).
\(M\left( {2\,;\,\,1} \right)\).
\(M\left( {2\,;\,\, - 1} \right)\).
Giá trị của \(a,\,\,b\) để \(x = 1\,;\,\,y = 4\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + \left( {a - 3} \right)y = - 2\\\left( {b - 2} \right)x + 3y = 13\end{array} \right.\) là
\(a = 2\,;\,\,b = 3\).
\(a = - 2\,;\,\,b = 3\).
\(a = 2\,;\,\,b = - 3\).
\(a = 2\,;\,\,b = - 3.\)
Gọi \(\left( {x\,;\,\,y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2\sqrt x + 3\sqrt {y - 3} = 18\\3\sqrt x - \sqrt {y - 3} = 5\end{array} \right.\). Giá trị của \(x + y\) là
26.
27.
28.
32.
Cho hệ phương trình \[\left\{ \begin{array}{l}2x + y = 5m - 1\\x - 2y = 2\end{array} \right.\]. Có bao nhiêu giá trị của \[m\] để hệ phương trình có nghiệm thỏa mãn \[{x^2} - 2{y^2} = - 2\]?
\(0\).
\(1\)
\(2\).
\(3\).
Dạng 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình \[9{x^2} - 1 - 2x\left( {3x - 1} \right) = 0\], khi đó
a) Phương trình có một nghiệm nguyên.
b) Phương trình có hai nghiệm là \[x = 1\,;\,\,\,x = \frac{1}{3}\].
c) Tổng hai nghiệm của phương trình là \(\frac{{ - 2}}{3}\).
d) Tích hai nghiệm của phương trình là \(\frac{2}{3}\).
Cho phương trình \[\frac{{2x + m}}{{x - 1}} = \frac{{5\left( {x - 1} \right)}}{{x + 1}}\] (với \(m\) là tham số).
a) Phương trình đã cho là phương trình chứa ẩn ở mẫu.
b) Khi \(x = 1\) và \(x = - 1\) thì phương trình đã cho không xác định.
c) Khi \[x = \frac{1}{3}\], ta thay vào phương trình đã cho ta tìm được \(m = - 1\).
d) Với \(m = - 2\) thì phương trình có nghiệm \[x = \frac{7}{3}.\]
Cho phương trình \(2x + 5y = 7\) có công thức nghiệm tổng quát là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = ax + b\end{array} \right.\).
a) Cặp số \(\left( {2;5} \right)\) là nghiệm của phương trình \(2x + 5y = 7\).
b) Áp dụng quy tắc chuyển vế ta thu được phương trình \(2x = 7 - 5y\).
c) Giá trị của hiệu \(a - b\) bằng \( - 1,8\).
d) Giá trị của tích \(ab\) bằng \[ - 5,6\].
Cho phương trình \(2x + y = 4.\)
a) Phương trình đã cho có vô nghiệm.
b) Các cặp số \(\left( {2\,;\,\,0} \right);\,\,\left( {0\,;\,\, - 4} \right)\) là nghiệm của phương trình \(2x + y = 4.\)
c) Phương trình đã cho là đường thẳng \(2x + y = 4\).
d) Đường thẳng \(2x + y = 4\) cắt trục hoành tại điểm có hoành độ là 2.
Cho phương trình \(\frac{1}{2}x - 2y = - 1\).
a) Cặp số \(\left( {2\,;\,\,1} \right)\) là nghiệm của phương trình đã cho.
b) Cặp số \(\left( {1\,;\,\,\frac{1}{4}} \right)\) không là nghiệm của phương trình đã cho.
c) Áp dụng quy tắc chuyển vế ta thu được phương trình \(2y = \frac{1}{2}x + 1\).
d) Công thức nghiệm của phương trình đã cho là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{1}{2}x + 1\end{array} \right.\).
Cho hệ phương trình \(\left\{ \begin{array}{l}x + 2 + \frac{2}{{\sqrt y - 3}} = 9\\2x + 4 - \frac{1}{{\sqrt y - 3}} = 8\end{array} \right.\) (I)
a) Điều kiện xác định của hệ phương trình (I) là \(\left\{ \begin{array}{l}y \ne 9\\y \ge 0\end{array} \right.\).
b) Đặt \(\frac{1}{{\sqrt y - 3}} = a\). Hệ phương trình (I) trở thành: O10-2024-GV154 O10-2024-GV147 \(\left\{ \begin{array}{l}(x + 2) + 2a = 9\\2(x + 2) - a = 8\end{array} \right.\) (II)
c) Giải hệ phương trình (II) ta được \(x = 3\,;\,\,a = 2.\)
d) Hệ phương trình (I) có nghiệm duy nhất \(\left( {x\,;\,\,y} \right) = \left( {3\,;\,\,\frac{7}{2}} \right)\).
Cho hệ phương trình \(\left\{ \begin{array}{l}x - y = m + 1\\2x + y = 5m + 2\end{array} \right.\) (\(m\) là tham số).
a) Phương trình \(x - y = m + 1\) là phương trình bậc nhất hai ẩn.
b) Nghiệm của hệ phương trình khi \(m = 2\) là \((x;\,\,y) = \left( {2;\,\,5} \right)\).
c) Biểu diễn \(x\,;\,\,y\) theo \(m\) được \(\left\{ \begin{array}{l}x = 2m + 1\\y = m\end{array} \right.\).
d) Với \(0 < m < 2\) thì hệ phương trình có nghiệm thoả mãn \(x > 1\,;\,\,y < 2\).
Trên một cánh đồng, người ta cấy 60 ha lúa giống mới và 40 ha lúa giống cũ, thu hoạch được tất cả 660 tấn thóc. Biết rằng 3 ha trồng lúa giống mới thu hoạch được ít hơn 4 ha trồng lúa giống cũ là 3 tấn. Gọi năng suất lúa giống mới và lúa giống cũ trên 1 ha lần lượt là \(x,\,\,y\) (đơn vị: tấn/ha).
a) Điều kiện \(x \in \mathbb{N}*,\,\,y \in \mathbb{N}*.\)
b) Tổng sản lượng thóc thu hoạch theo \(x,\,\,y\) là \(60x + 40y\) (tấn).
c) Phương trình \(3x - 4y = 3\) thể hiện 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 3 tấn.
d) Năng suất lúa mới trên 1 ha là 5 tấn.
Ba xe ô tô chở 118 tấn hàng tổng cộng hết 50 chuyến. Số chuyến xe thứ nhất chở gấp rưỡi số chuyến xe thứ hai. Mỗi chuyến xe thứ nhất chở 2 tấn, xe thứ hai chở 2,5 tấn, xe thứ ba chở 3 tấn.
a) Ô tô thứ nhất chở ít chuyến hơn ô tô thứ hai.
b) Mỗi chuyến, ô tô thứ hai chở được ít hàng nhất.
c) Tổng số hàng (tấn) ô tô thứ ba chở bằng \(\frac{5}{8}\) tổng số hàng ô tô thứ nhất chở.
d) Nếu ô tô thứ ba chở hộ số hàng (tấn) mà ô tô thứ hai chở trong 2 chuyến thì số hàng hai ô tô chở được bằng nhau.
Trong một kì thi, hai trường A, B có tổng cộng 350 học sinh dự thi. Kết quả hai trường đó có 338 học sinh trúng tuyển. Tính ra thì trường A có 97% và trường B có 96% số học sinh trúng tuyển. Hỏi trường B có bao nhiêu học sinh dự thi.
a) Tỉ lệ trúng tuyển của trường A cao hơn trường B.
b) Số học không trúng tuyển của hai trường là 12 học sinh.
c) Phương trình thể hiện số học sinh trúng tuyển của hai trường đạt là \[97x + 96y = 338.\]
d) Trường A có 150 thí sinh dự thi.
Dạng 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Cho phương trình \(\frac{1}{{x + 1}} - \frac{{2{x^2} - m}}{{{x^3} + 1}} = \frac{4}{{{x^2} - x + 1}}\). Biết \(x = 0\) là một nghiệm của phương trình. Hỏi nghiệm còn lại có giá trị bằng bao nhiêu?
Cho hai biểu thức \[A = \frac{3}{{3x + 1}} + \frac{2}{{1 - 3x}}\] và \[B = \frac{{x - 5}}{{9{x^2} - 1}}.\] Có bao nhiêu giá trị nào của \[x\] để hai biểu thức \[A\] và \[B\] có cùng một giá trị?
Bác An có một mảnh đất hình chữ nhật với chiều dài \[14\,\,{\rm{m}}\] và chiều rộng \[12\,\,{\rm{m}}.\] Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích để làm sân vườn như hình vẽ. Biết diện tích đất làm nhà là \(100\,\,{{\rm{m}}^{\rm{2}}}\). Hỏi \(x\) bằng bao nhiêu mét?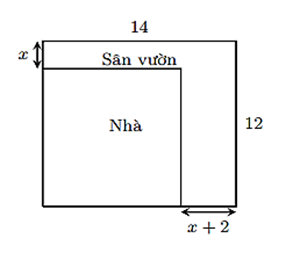
Một doanh nghiệp sử dụng than để sản xuất. Doanh nghiệp đó lập kế hoạch tài chính cho viẹc loại bỏ chất ô nhiễm trong khí thải theo dự kiến sau: Để loại bỏ \(p\% \) chất ô nhiễm trong khí thải thì chi phí \(C\) (triệu đồng) được tính theo công thức \(C = \frac{{80}}{{100 - p}}\), với \(0 \le p < 100\). Với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được bao nhiêu phầm trăm chất gây ô nhiễm trong khí thải (làm tròn kết quả đến hàng phần mười).
Một công nhân dự kiến làm \[33\] sản phẩm trong một thời gian nhất định. Trước khi thực hiện, xí nghiệp giao thêm cho công nhân đó \[29\] sản phẩm nữa. Do đó mặc dù mỗi giờ công nhân đó đã làm thêm \[3\] sản phẩm nhưng vẫn hoàn thành chậm hơn dự kiến \[1\] giờ \[30\] phút. Năng suất dự kiến của công nhân đó là bao nhiêu sản phẩm/giờ?
Cho hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\3x - 2y = 0\end{array} \right.\) có nghiệm là \(\left( {x;y} \right)\). Tính giá trị biểu thức \({x^2} + 2xy + {y^2}.\)
Tìm nghiệm nguyên âm lớn nhất của phương trình \( - 5x + 2y = 7\). Kết quả là \(x = a\,;\,\,y = b\). Tính \[a + b.\]
Phương trình đường thẳng \(\left( d \right):mx + 2y = 4\)O10-2024-GV154O10-2024-GV147 đi qua điểm cố định \(M\). Tính tổng các toạ độ của điểm \(M.\)
Tìm hệ số \[x\] trong phản ứng hoá học đã được cân bằng sau:
\(4{\rm{P}} + x\,{{\rm{O}}_2} \to y\,{{\rm{P}}_2}{{\rm{O}}_5}\).
Cho hệ phương trình \(\left\{ \begin{array}{l}x + y = 6\\{x^2} + {y^2} = 20\end{array} \right.\) biết hệ có hai nghiệm \(\left( {x\,;\,\,y} \right)\) trong đó có một nghiệm là \(\left( {2\,;\,\,4} \right).\) Tính tổng \(3x + 2y\) nếu \(x > y\).
Với giá trị nào của a thì hệ phương trình \[\left\{ \begin{array}{l}x + y = {a^2} + a + 1\\x - y =- {a^2} + a - 1\end{array} \right.\] có nghiệm \(\left( {x\,;\,\,y} \right)\) với \(3x + y\) nhỏ nhất? (viết kết quả dưới dạng số thập phân)
Cho hệ phương trình \(\left\{ \begin{array}{l}x + y = 2m\\{x^2} + {y^2} = 2m + 2\end{array} \right.\)với cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ. Tính giá trị của \(m\) để biểu thức \(P = {x_0}{y_0} - 3\left( {{x_0} + {y_0}} \right)\) đạt giá trị nhỏ nhất (viết kết quả dưới dạng số thập phân).
Qua nghiên cứu, người ta nhận thấy rằng với mỗi người trung bình nhiệt độ môi trường giảm đi \[1^\circ {\rm{C}}\]thì lượng calo cần tăng thêm khoảng \[30\] calo. Tại \[21^\circ {\rm{C}}\], một người làm việc cần sử dụng khoảng 3000 calo mỗi ngày. Người ta thấy mối quan hệ giữa hai đại lượng này là một hàm số bậc nhất \[y = ax + b\] (\[x\] là đại lượng biểu thị cho nhiệt độ môi trường và \[y\]là đại lượng biểu thị cho lượng calo). Nếu một người làm việc ở sa mạc Sahara trong nhiệt độ \[50^\circ {\rm{C}}\] thì cần bao nhiêu calo?
Hai vòi nước cùng chảy vào một bể thì bể sẽ đầy trong \[4\] giờ \(48\) phút. Người ta cho vòi I chảy trong \[4\] giờ rồi khóa vòi thứ nhất, vòi thứ hai tiếp tục chảy trong \(2\) giờ thì được \(\frac{2}{3}\) bể. Thời gian vòi I chảy một mình đầy bể là bao nhiêu?
Một mảnh đất hình chữ nhật có chu vi \[56{\rm{\;m}}{\rm{.}}\] Nếu tăng chiều rộng thêm \[2{\rm{\;m}}\] và giảm chiều dài đi \[{\rm{1\;m}}\] thì diện tích của mảnh đất tăng thêm \[18{\rm{\;}}{{\rm{m}}^2}.\] Tính diện tích mảnh đất đó. (đơn vị: \[{{\rm{m}}^2}).\]


