Bài tập ôn tập Toán 12 Chân trời sáng tạo Chương 6 có đáp án
51 câu hỏi
A. Trắc nghiệm
Dạng 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hai biến cố \(A\) và \(B\) có\(P\left( A \right) = 0,3;P\left( B \right) = 0,6;\,P\left( {A \cap B} \right) = 0,2.\)Xác suất \(P\left( {A|B} \right)\)là
\(\frac{1}{2}\).
\(\frac{1}{3}\).
\(\frac{2}{3}\).
\(\frac{1}{6}\).
Từ một hộp có 4 tấm thẻ cùng loại được ghi số lần lượt từ 1 đến 4. Bạn An lấy ra một cách ngẫu nhiên một thẻ từ hộp, bỏ thẻ đó ra ngoài và lại lấy một cách ngẫu nhiên thêm một thẻ nữa. Xét biến cố \(A\) là “thẻ lấy ra lần thứ nhất ghi số 3”. Số các kết quả thuận lợi của biến cố \(A\) là
\(3\).
\(2\)
\(4\).
\(1\).
Gieo con xúc xắc 1 lần. Gọi A là biến cố xuất hiện mặt 2 chấm, B là biến cố xuất hiện mặt chẵn. Xác suất \(P\left( {A|B} \right)\)là
\(\frac{1}{2}\).
\(\frac{1}{3}\).
\(\frac{2}{3}\).
\(\frac{1}{6}\).
Cho hai biến độc lập \(A,B\) với \(P\left( A \right) = 0,8;{\rm{ }}P\left( B \right) = 0,3\). Khi đó, \(P\left( {A\left| B \right.} \right)\)bằng
\(0,8\).
\(0,3\).
\(0,4\).
\(0,6\).
Nếu hai biến cố \(A,{\kern 1pt} {\kern 1pt} B\) thỏa mãn \(P\left( A \right) = 0,4;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P\left( {B|A} \right) = 0,6\) thì \(P\left( {A \cap B} \right)\) bằng:
\(\frac{6}{{25}}\).
\(\frac{2}{3}\).
\(\frac{1}{5}\).
\(1\).
Nếu hai biến cố \(A,{\kern 1pt} {\kern 1pt} B\) thỏa mãn \(P\left( B \right) = 0,7;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P\left( {A \cap B} \right) = 0,2\) thì \(P\left( {A|B} \right)\) bằng:
\(\frac{5}{7}\).
\(\frac{1}{2}\).
\(\frac{7}{{50}}\).
\(\frac{2}{7}\).
Cho hai biến cố \(A\) và \(B\) với \[P\left( B \right) = 0,5\], \(P\left( {A \cap B} \right) = 0,2\). Tính \(P\left( {\bar A|B} \right)\).
\(0,4\).
\(0,1\).
\(0,6\).
\(0,3\).
Nếu hai biến cố \(A,{\kern 1pt} {\kern 1pt} B\) thỏa mãn \(P\left( B \right) = 0,5;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P\left( {AB} \right) = 0,3\) thì \(P\left( {\overline A B} \right)\) bằng:
\(\frac{3}{{20}}\).
\(\frac{4}{5}\).
\(\frac{1}{5}\).
\(\frac{3}{5}\).
Một công ty xây dựng đấu thầu hai dự án độc lập. Khả năng thắng của dự án thứ nhất là \(0,5\) và dự án thứ hai là \(0,6\). Tính xác suất để công ty thắng thầu dự án thứ hai biết công ty thắng thầu dự án thứ nhất.
\(0,3\).
\(0,7\).
\(0,5\).
\(0,6\).
Gieo một con xúc xắc cân đối và đồng chất. Tính xác suất số chấm trên con xúc xắc không nhỏ hơn \[4\], biết rằng con xúc xắc xuất hiện mặt lẻ.
\[\frac{1}{6}\].
\[\frac{2}{3}\].
\[\frac{1}{3}\].
\[\frac{1}{2}\].
Lớp 10A có 45 học sinh trong đó có 20 học sinh nam và 25 học sinh nữ. Trong bài kiểm tra môn Toán cả lớp có 22 học sinh đạt điểm giỏi (trong đó có 10 học sinh nam và 12 học sinh nữ). Giáo viên chọn ngẫu nhiên một học sinh từ danh sách lớp. Tính xác suất để giáo viên chọn được một học sinh đạt điểm giỏi môn Toán biết học sinh đó là học sinh nam.
\(\frac{1}{2}\).
\(\frac{4}{5}\).
\(\frac{3}{5}\).
\(\frac{4}{{15}}\).
Một cửa hàng thời trang ước lượng rằng có \[86\% \]khách hàng đến cửa hàng mua quần áo là phụ nữ, và có \[25\% \]số khách mua hàng là phụ nữ cần nhân viên tư vấn. Biết một người mua quần áo là phụ nữ, tính xác suất người đó cần nhân viên tư vấn.
\[\frac{1}{4}\].
\[0,86\].
\[\frac{{30}}{{43}}\].
\[\frac{{25}}{{86}}\].
Cho hai biến cố \(A,\,B\)với \(P\left( B \right) = 0,8;P\left( {A|B} \right) = 0,5\).Tính \[P\left( {AB} \right)\].
\(\frac{3}{7}\).
\(0,4\)
\(0,8\).
\(0,5\).
Cho hai biến cố \[A\] và \[B\] có \[P\left( A \right) = 0,3\], \[P\left( B \right) = 0,7\] và \[P\left( {A|B} \right) = 0,5\]. Tính \[P\left( {\overline A B} \right)\].
\[0,35\].
\[0,3\].
\[0,65\].
\[0,55\].
Cho hai biến cố \(A\) và \(B\) có \(P\left( A \right) = 0,2;\,\,\,P\left( B \right) = 0,8\) và \(P\left( {A|B} \right) = 0,5\). Tính \(P\left( {\overline A B} \right)\) có kết quả là
\(P\left( {\overline A B} \right) = 0,9\).
\(P\left( {\overline A B} \right) = 0,6\).
\(P\left( {\overline A B} \right) = 0,04\).
\(P\left( {\overline A B} \right) = 0,4\).
Một hộp chứa 8 bi xanh, 2 bi đỏ. Lần lượt bốc từng bi. Giả sử lần đầu tiên bốc được bi xanh. Xác định xác suất lần thứ 2 bốc được bi đỏ.
\(\frac{1}{{10}}\)
\(\frac{2}{9}\).
\(\frac{8}{9}\).
\(\frac{2}{5}\).
Cho hai biến cố \(A\) và \(B\) với \(0 < P\left( B \right) < 1\). Khẳng định nào sau đây là đúng?
\[P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\overline B } \right)P\left( {A|\overline B } \right)\].
\[P\left( A \right) = P\left( A \right)P\left( {A|B} \right) + P\left( {\overline A } \right)P\left( {A|\overline B } \right)\].
\[P\left( A \right) = P\left( B \right)P\left( {A|\overline B } \right) + P\left( {\overline B } \right)P\left( {A|B} \right)\].
\[P\left( A \right) = P\left( B \right)P\left( {A|B} \right) - P\left( {\overline B } \right)P\left( {A|\overline B } \right)\].
Cho hai biến cố \[A,\,B\] thỏa mãn \[P\left( A \right) = 0,4;\,P\left( {A|B} \right) = 0,5;\,P\left( {\left. A \right|\overline B } \right) = 0,1\]. Khi đó, \[P\left( B \right)\] bằng
\(0,9\).
\(0,25\).
\(0,2\).
\(0,75\).
Cho hai biến cố \[A\] và \[B\]. Biết \[P\left( B \right) = 0,01\]; \[P\left( {A|B} \right) = 0,7\]; \[P\left( {A|\overline B } \right) = 0,09\]. Khi đó \[P\left( A \right)\] bằng
\(0,0079\).
\(0,0961\).
\(0,0916\).
\(0,0970\).
Cho hai biến cố \(A,B\) với \(P\left( B \right) = 0,6\), \(P\left( {A|B} \right) = 0,7\) và \(P\left( {A|\bar B} \right) = 0,4\). Khi đó, \(P\left( A \right)\) bằng
\(0,7\).
\(0,4\).
\(0,58\).
\(0,52\).
Cho hai biến cố \[A\] và \[B\], với \[P\left( A \right) = 0,2\], \[P\left( {B|A} \right) = 0,7\], \[P\left( {B|\overline A } \right) = 0,15\]. Tính \[P\left( {A|B} \right)\].
\[\frac{7}{{13}}\].
\[\frac{6}{{13}}\].
\[\frac{4}{{13}}\].
\[\frac{9}{{13}}\].
Hai máy tự động sản xuất cùng một loại chi tiết, trong đó máy I sản xuất \[35\% ,\]máy II sản xuất \[65\% \]tổng sản lượng. Tỉ lệ phế phẩm của các máy lần lượt là \[0,3\% \]và \[0,7\% .\]Chọn ngẫu nhiên \(1\) sản phẩm từ kho. Tính xác suất để chọn được phế phẩm?
\(0,0056\).
\(0,0065\).
\(0,065\).
\(0,056\).
Giả sử \(A\) và \(B\) là hai biến cố ngẫu nhiên thỏa mãn \(P\left( A \right) > 0\) và \(0 < P\left( B \right) < 1\). Khẳng định nào dưới đây sai?
\(P\left( {B|A} \right) = \frac{{P\left( B \right)P\left( {A|B} \right)}}{{P\left( B \right)P\left( {A|B} \right) + P\left( A \right)P\left( {B|A} \right)}}\).
\(P\left( {B|A} \right) = \frac{{P\left( B \right)P\left( {A|B} \right)}}{{P\left( B \right)P\left( {A|B} \right) + P\left( {\overline B } \right)P\left( {A|\overline B } \right)}}\).
\(P\left( {B|A} \right) = \frac{{P\left( B \right)P\left( {A|B} \right)}}{{P\left( A \right)}}\).
\(P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\overline B } \right)P\left( {A|\overline B } \right)\).
Người ta điều tra thấy ở một địa phương nọ có \(3\% \) tài xế sử dụng điện thoại di động khi lái xe. Người ta nhận thấy khi tài xế lái xe gây ra tai nạn thì có \(21\% \) là do tài xế sử dụng điện thoại. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?
\(3\).
\(7\).
\(5\).
\(6\).
Cho hai biến cố \(A\) và \(B\) sao cho \(P\left( A \right) = 0,6\); \(P\left( B \right) = 0,4\); \(P\left( {A|B} \right) = 0,3\). Khi đó \(P\left( {B|A} \right)\) bằng
\(0,2\).
\(0,3\).
\(0,4\).
\(0,6\).
Cho hai biến cố \[A\] và \[B\]. Biết rằng \[P\left( B \right) = 0,8\]; \[P\left( {A|B} \right) = 0,7\] và \[P\left( {A|\bar B} \right) = 0,45\]. Khi đó giá trị của \[P\left( {B|A} \right)\] bằng
\[0,25\].
\[0,65\].
\[\frac{{56}}{{65}}\].
\[0,5\].
Dạng 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho sơ đồ hình cây như hình dưới đây.
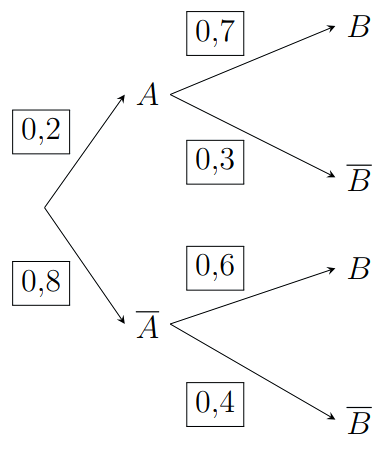
a) \[P\left( B \right) = P\left( A \right).P\left( {B\mid A} \right) + P\left( {\bar A} \right).P\left( {B\mid \bar A} \right)\].
b) \(P\left( {B\mid A} \right) = 0{\rm{,}}6\).
c) \(P\left( B \right) = 0{\rm{,}}62\).
d) \(P\left( {\bar B} \right) = 0{\rm{,}}4\).
Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ còn lại là nam. Có 3 bạn tên Hiền, trong đó có 1 bạn nữ và 2 bạn nam. Thầy giáo gọi ngẫu nhiên 1 bạn lên bảng.
a) Xác suất để gọi một bạn tên Hiền là \(\frac{1}{{10}}\).
b) Xác suất để có tên Hiền, nhưng với điều kiện bạn đó giới tính nữ là \(\frac{3}{{17}}\).
c) Xác suất để có tên Hiền, nhưng với điều kiện bạn đó giới tính nam là \(\frac{2}{{13}}\).
d) Nếu thầy giáo gọi một bạn tên Hiền lên bảng thì xác suất để bạn đó mang giới tính nữ là \(\frac{3}{{17}}\).
Hình dạng hạt của đậu Hà Lan có hai kiểu hình: hạt trơn và hạt nhăn, có hai gene ứng với hai kiểu hình này là gene trội B và gene lặn b. Khi cho lai hai cây đậu Hà Lan, cây con lấy ngẫu nhiên một cách độc lập một gene từ cây bố và một gene từ cây mẹ để hình thành một cặp gene. Giả sử cây bố và cây mẹ được chọn ngẫu nhiên từ một quần thể các cây đậu Hà Lan, ở đó tỉ lệ cây mang kiểu gene bb, Bb tương ứng là \(40\% \) và \(60\% \).
a) Xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene bb là \(0,5\).
b) Xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene Bb là \(0,5\).
c) Xác suất để cây con lấy gene b từ cây bố là \(0,6\).
d) Xác suất để cây con có kiểu gene bb là \(0,49\).
Một cửa hàng chỉ bán hai loại điện thoại là Samsung và Iphone. Tỷ lệ khách hàng mua điện thoại Samsung là \(75\% \). Trong số các khách hàng mua điện thoại Samsung thì có \(60\% \) mua kèm ốp điện thoại. Tỷ lệ khách hàng mua điện thoại Iphone kèm ốp điện thoại trong số những khách hàng mua điện thoại Iphone là \(30\% .\)
a) Xác suất một khách hàng mua điện thoại Samsung là \(0,75\).
b) Xác suất để một khách hàng mua điện thoại Iphone là \(0,15\).
c) Xác suất để một khách hàng mua ốp điện thoại biết rằng khách hàng đó đã mua điện thoại Samsung là \(0,6\), xác suất để một khách hàng mua ốp điện thoại biết rằng khách hàng đó đã mua Iphone là \(0,3\).
d) Xác suất một khách hàng mua điện thoại kèm ốp là \(0,525\).
Có hai chiếc hộp. Hộp thứ nhất có \[5\] viên bi xanh và \[7\] viên bi đỏ. Hộp thứ hai có \[6\] viên bi xanh và \[8\] viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên \[1\] viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời \[2\] viên bi từ hộp thứ hai. Gọi \[A\] là biến cố “Lấy được 1 viên bi màu xanh ở hộp thứ nhất” và \[B\] là biến cố “Lấy được 2 viên bi màu đỏ ở hộp thứ hai”.
a) \(P\left( {\overline A } \right) = \frac{5}{{12}}\).
b) \[P\left( {B|A} \right) = \frac{1}{{15}}\].
c) \[P\left( {B|\overline A } \right) = \frac{{12}}{{35}}\].
d) \(P\left( B \right) = \frac{{14}}{{45}}\).
Trong năm học vừa qua, ở trường đại học X, tỉ lệ sinh viên thi trượt môn Toán là \(30\% \), thi trượt môn Tâm lý là \(22\% \). Trong số các sinh viên trượt môn Toán có \(40\% \)sinh viên trượt môn Tâm lý. Gặp ngẫu nhiên một sinh viên trường X.
a) Xác suất gặp sinh viên trượt cả hai môn Toán và Tâm lý là \(0,066\).
b) Xác suất gặp sinh viên đậu cả hai môn Toán và Tâm lý là \(0,6\).
c) Xác suất gặp sinh viên đậu môn Toán biết rằng sinh viên này trượt môn Tâm lý là \(0,18\).
d) Xác suất gặp sinh viên đậu môn Tâm lý là \(0,726\).
Chạy Marathon là môn thể thao mà tại đó, người chơi sẽ hoàn thành quãng đường 42,195 km trong khoảng thời gian nhất định. FM sub 4 là thành tích dành cho những người chơi hoàn thành quãng đường Marathon dưới 4 giờ. Trong CLB AKR, tỷ lệ thành viên nam là \[72\% \], tỷ lệ thành viên nữ là \[28\% \]. Đối với nam, tỷ lệ VĐV hoàn thành Marathon sub 4 là \[32\% \]; đối với nữ tỷ lệ VĐV hoàn thành sub 4 là \[3\% \]. Chọn ngẫu nhiên 1 thành viên từ CLB AKR.
a) Khi VĐV được chọn là nam, xác suất để VĐV này chưa hoàn thành sub 4 cự ly Marathon là \[68\% \].
b) Xác suất để thành viên được chọn đã hoàn thành sub 4 là \[22\% \].
c) Xác suất để thành viên được chọn là nữ đã hoàn thành sub 4 là \[2\% \].
d) Biết rằng VĐV được chọn đã hoàn thành sub 4, xác suất để VĐV đó là nam bằng \[96\% \].
Có hai đội thi đấu môn bắn súng. Đội I có 8 vận động viên, đội II có 10 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,6 và 0,55. Chọn ngẫu nhiên một vận động viên.
a) Xác suất để vận động viên chọn ra thuộc đội I là \(\frac{5}{9}\).
b) Xác suất không đạt huy chương vàng của mỗi vận động viên đội II là \(0,45\).
c) Xác suất để vận động viên này đạt huy chương vàng là \(\frac{{103}}{{180}}\).
d) Giả sử vận động viên được chọn đạt huy chương vàng. Xác suất để vận động viên này thuộc đội I là \(\frac{{48}}{{103}}\).
Một doanh nghiệp có 45% nhân viên là nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là 7% và 5%. Chọn ngẫu nhiên một nhân viên của doanh nghiệp.
a) Xác suất nhân viên được chọn có mua bảo hiểm nhân thọ là \(0,061\).
b) Biết rằng nhân viên được chọn có mua bảo hiểm nhân thọ. Xác suất nhân viên đó là nam là \(\frac{{55}}{{118}}\).
c) Biết rằng nhân viên được chọn có mua bảo hiểm nhân thọ. Xác suất nhân viên đó là nữ là \(\frac{{63}}{{118}}\)
d) Biết rằng nhân viên được chọn có mua bảo hiểm nhân thọ. Khi đó nhân viên đó là nam nhiều hơn là nữ.
Một kho hàng có 1000 thùng hàng với bề ngoài giống hệt nhau, trong đó có 480 thùng hàng loại I và 520 thùng hàng loại II. Trong số các thùng hàng đó, có \(80\% \) thùng hàng loại I và \(85\% \) thùng hàng loại II đã được kiểm định. Chọn ngẫu nhiên một thùng hàng trong kho.
a) Xác suất chọn được thùng hàng loại I bằng \(48\% \).
b) Xác suất chọn được thùng hàng loại II đã được kiểm định bằng 38,4%.
c) Xác suất chọn được thùng hàng chưa kiểm định bằng 17,4%.
d) Giả sử thùng hàng được lấy ra là thùng hàng chưa được kiểm định, xác suất thùng hàng đó là thùng loại I thấp hơn xác suất thùng hàng đó là thùng loại II.
Dạng 3. Trắc nghiệm trả lời ngắn
Một hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 90% số viên bi màu đỏ được đánh số và 50% số viên bi màu vàng được đánh số, những viên bi còn lại không đánh số. Lấy ra ngẫu nhiên một viên bi trong hộp. Tính xác suất để viên bi được lấy ra có đánh số (kết quả để dưới dạng số thập phân và làm tròn đến hàng phần trăm).
Số khán giả đến xem buổi biểu diễn âm nhạc ngoài trời phụ thuộc vào thời tiết. Giả sử, nếu trời không mưa thì xác suất để bán hết vé là 0,85; còn nếu trời mưa thì xác suất để bán hết vé là 0,45. Dự báo thời tiết cho thấy nếu xác suất để trời mưa vào buổi biểu diễn là 0,6. Tính xác suất để nhà tổ chức sự kiện bán hết vé.
Tỉ lệ bị bệnh cúm tại một địa phương bằng \(0,25\). Khi thực hiện xét nghiệm chẩn đoán, nếu người có bệnh cúm thì khả năng phản ứng dương tính là \(96\% \), nếu người không bị bệnh cúm thì khả năng phản ứng dương tính \(8\% \). Chọn ngẫu nhiên 1 người tại địa phương đó. Xác suất người được chọn có phản ứng dương tính là bao nhiêu?
Có hai hộp bóng bàn, các quả bóng bàn có kích thước và hình dạng như nhau. Hộp thứ nhất có 3 quả bóng bàn màu trắng và 2 quả bóng bàn màu vàng. Hộp thứ hai có 6 quả bóng bàn màu trắng và 4 quả bóng bàn màu vàng. Lấy ngẫu nhiên 4 quả bóng bàn ở hộp thứ nhất bỏ vào hộp thứ hai rồi lấy ngẫu nhiên 1 quả bóng bàn ở hộp thứ hai ra. Tính xác suất để lấy được quả bóng bàn màu vàng từ hộp thứ hai.
Thống kê hồ sơ 250 học sinh khối 10 trong đó có 150 học sinh nữ và 100 học sinh nam. Sau khi thống kê, kết quả có \(60\% \) học sinh nữ là đoàn viên, \(50\% \) học sinh nam là đoàn viên; những học sinh còn lại không là đoàn viên. Chọn ngẫu nhiên một học sinh trong 250 học sinh khối 10. Tính xác suất để học sinh được chọn là đoàn viên.
Một đội bắn súng gồm có 8 nam và 2 nữ. Xác suất bắn trúng của các xạ thủ nam là 0,8 còn của các xạ thủ nữ là 0,9. Chọn ngẫu nhiên một xạ thủ bắn một viên đạn và xạ thủ đó đã bắn trúng. Tính xác suất (làm tròn đến hàng phần trăm) để xạ thủ đó là nữ?
Trước khi đưa sản phẩm ra thị trường, người ta đã phỏng vấn ngẫu nhiên 200 khách hàng về sản phẩm đó và thấy có 50 người trả lời “sẽ mua”, 90 người trả lời “có thể sẽ mua” và 60 người trả lời “không mua”. Kinh nghiệm cho thấy tỷ lệ khách hàng thực sự sẽ mua sản phẩm tương ứng với những cách trả lời trên tương ứng là 60%, 40% và 1%. Trong số khách hàng thực sự mua sản phẩm thì xác suất khách hàng trả lời “sẽ mua” là \[\frac{a}{b}\] (với \[\frac{a}{b}\] là phân số tối giản). Tính giá trị của biểu thức \[T = a + \frac{1}{2}b.\]
Một nhà máy sản xuất pin điện thoại có 2 dây chuyền sản xuất. Dây chuyền I tạo ra 65% sản phẩm của toàn nhà máy; dây chuyền II tạo ra 35% sản phẩm của toàn nhà máy. Trong số các sản phẩm được sản xuất từ dây chuyền I có 3% sản phẩm bị lỗi, trong số các sản phẩm được sản xuất từ dây chuyền II có 2% sản phẩm bị lỗi. Chọn ngẫu nhiên một sản phẩm của nhà máy, gọi xác suất để sản phẩm đó là sản phẩm bị lỗi và được sản xuất từ dây chuyền I bằng P. Tính 1000P.
Một công ty du lịch bố trí chỗ nghỉ cho đoàn khách tại ba khách sạn \[A,\,B,\,C\] theo tỉ lệ \[20\]%, \[50\]%, \[30\]%. Tỉ lệ hỏng điều hòa ở ba khách sạn lần lượt là \[5\]%, \[4\]%, \[8\]%. Tính xác suất để một khách ở khách sạn \[C\], biết khách đó ở phòng điều hòa không bị hỏng (kết quả để dưới dạng số thập phân và làm tròn đến hàng phần trăm).
Trường X có \(20\% \) học sinh tham gia câu lạc bộ thể thao, trong số học sinh đó có \(85\% \) học sinh biết chơi môn bóng bàn. Ngoài ra, có \(10\% \) số học sinh không tham gia câu lạc bộ thể thao cũng biết chơi môn bóng bàn. Chọn ngẫu nhiên \(1\) học sinh của trường. Giả sử học sinh đó biết chơi môn bóng bàn. Xác suất chọn được học sinh thuộc câu lạc bộ thể thao là \(\frac{a}{b}\)(với \[\frac{a}{b}\] là phân số tối giản). Tính \(a - b\).
B. Tự luận
Kết quả khảo sát những bệnh nhân là học sinh bị tai nạn xe máy điện về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:
Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là \(60\% \).
Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là \(90\% \).
Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách và bị chấn thương vùng đầu là \(15\% \).
Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách đối với học sinh khi di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn bao nhiêu lần?
Một công ty bảo hiểm nhận thấy có \(52\% \) số người mua bảo hiểm ô tô là đàn ông và có \(39\% \) số người mua bảo hiểm ô tô là đàn ông trên 40 tuổi.
a) Biết một người mua bảo hiểm ô tô là đàn ông, tính xác suất người đó trên 40 tuổi.
b) Tính tỉ lệ người trên 40 tuổi trong số những người đàn ông mua bảo hiểm ô tô.
Có hai cái hộp. Hộp thứ nhất có 4 bi trắng và 5 bi đen. Hộp thứ hai có 5 bi trắng và 4 bi đen. Chọn ngẫu nhiên 3 viên bi ở hộp thứ nhất bỏ vào hộp thứ hai rồi sau đó chọn ngẫu nhiên 1 viên bi ở hộp thứ hai. Khi đó xác suất để lấy được bi trắng là bao nhiêu?
Một loại linh kiện do hai nhà máy số I và số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I và II lần lượt là \(4\% \) và \(3\% \). Trong một lô linh kiện để lẫn lộn \(80\) sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó. Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao hơn?
Trong trò chơi hái hoa có thưởng của lớp 10A, cô giáo treo 10 bông hoa trên cành cây, trong đó có 5 bông hoa chứa phiếu có thưởng. Bạn Việt hái một bông hoa đầu tiên sau đó bạn Nam hái bông hoa thứ hai. Tính xác suất bạn Nam hái được bông hoa chứa phiếu có thưởng.


