7 câu hỏi
Cho ∆ABC có AB = AC. Gọi AM là tia phân giác của (M ∈ BC). Kẻ MD vuông góc AB (D ∈ AB) và ME vuông góc với AC (E ∈ AC).
Cho các khẳng định sau:
(I) ;
(II) ∆MBD = ∆MCE;
(III) AD = AE ;
Gọi m là số kết luận đúngvà n là số kết luận sai. Giá trị của m và n là:
m = 0 và n = 1;
m = 2 và n = 1;
m = 3 và n = 0;
m = 1 và n = 2.
Cho ∆ABC có AB = AC (). Kẻ BD vuông góc với AC (D ∈ AC) và CE vuông góc với AB (E ∈ AB). Gọi H là giao điểm của BD và CE.
Cho bảng sau:
|
A |
B |
|
a. ∆AEC |
1. ∆HDC |
|
b. ∆HEB |
2. ∆CDB |
|
c. ∆BEC |
3. ∆ADB |
Ghép các ý ở cột A với cột B để được một đẳng thức đúng?
a – 2; b – 1; c – 3;
a – 1; b – 3; c – 2;
a – 3; b – 1; c – 2;
a – 2; c – 1; b – 3.
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Kết luận nào sau đây sai?
AM = DM;
∆ABM =∆ADM ;
;
A, B, C sai.
Cho tam giác ABC có AD vuông góc với BC. Biết AB = AC = 3cm, . Tính cạnh BC.
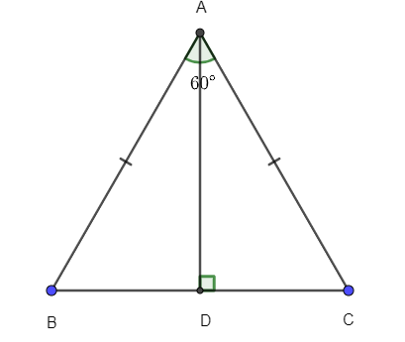
BC = 6 cm;
BC = 1,5 cm;
BC = 9 cm;
BC = 3cm.
Cho hình vẽ bên.
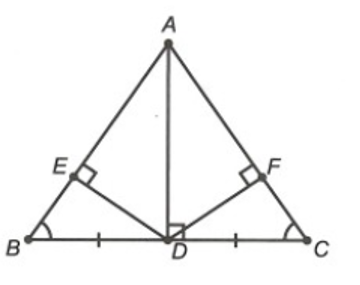
Khẳng định nào sau đây sai?
∆AED = ∆AFD;
∆BED = ∆CFD;
∆ADB = ∆ADC;
∆ADE = ∆AFD.
Cho ∆ABC có AB = AC và . Trên cạnh BC, lấy hai điểm D và E sao cho BD = EC. Kẻ DM vuông góc với AB (M ∈ AB) và EN vuông góc với AC (N ∈ AC). Kết luận nào sau đây đúng nhất?
∆AMD = ∆ANE;
∆ABD = ∆ACE;
MD = EN;
Cả A, B, C đều đúng.
Cho đoạn thẳng BC và điểm H nằm giữa B và C. Qua H kẻ đường thẳng vuông góc với BC. Trên đường thẳng đó lấy các điểm A và K sao cho HA = HK. Kẻ các đoạn thẳng AB, BK, KC, CA. Kết luận nào sau đây sai?
BA = BK
;
;
∆AHB = ∆KHB.
