23 CÂU HỎI
Cho hàm số \[F(x)\] là một nguyên hàm của hàm số \[f(x)\] trên \[K\]. Các mệnh đề sau, mệnh đề nào sai.
\[\int {f(x)dx = } F(x) + C\].
\({\left( {\int {f(x)dx} } \right)^\prime } = f(x)\).
\({\left( {\int {f(x)dx} } \right)^\prime } = f'(x)\).
\({\left( {\int {f(x)dx} } \right)^\prime } = F'(x)\).
Cho hàm số \[F(x)\] là một nguyên hàm của hàm số \[f(x)\] trên ... Các mệnh đề sau, mệnh đề nào sai.
C. \({\left( {\int {f(x)dx} } \right)^\prime } = f'(x)\).
\[\int {f(x)dx = } F(x) + C\].
B.
\({\left( {\int {f(x)dx} } \right)^\prime } = f(x)\).
\({\left( {\int {f(x)dx} } \right)^\prime } = F'(x)\).
Cho hàm số \[F(x)\] là một nguyên hàm của hàm số \[f(x)\] trên ... Các mệnh đề sau, mệnh đề nào sai.
\[\int {f(x)dx = } F(x) + C\].
\({\left( {\int {f(x)dx} } \right)^\prime } = f(x)\).
\({\left( {\int {f(x)dx} } \right)^\prime } = f'(x)\).
\({\left( {\int {f(x)dx} } \right)^\prime } = F'(x)\).
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = 2x + 6\) là
\[{x^2} + C\].
B.\[{x^2} + 6x + C\].
C.
\[2{x^2} + C\].
D.
\[2{x^2} + 6x + C\].
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = 2x + 6\) là
\[{x^2} + C\].
\[{x^2} + 6x + C\].
\[2{x^2} + C\].
\[2{x^2} + 6x + C\].
\(\int {{x^2}dx} \) bằng
\(2x + C\).
B.\(\frac{1}{3}{x^3} + C\).
C.
\({x^3} + C\).
D.
\(3{x^3} + C\)
\(\int {{x^2}dx} \) bằng
\(2x + C\).
\(\frac{1}{3}{x^3} + C\).
\({x^3} + C\).
\(3{x^3} + C\)
Họ nguyên hàm của hàm số \(f(x) = 3{x^2} + 1\) là
\({x^3} + C\)
B.
\(\frac{{{x^3}}}{3} + x + C\)
C.
\(6x + C\)
D.\({x^3} + x + C\)
Họ nguyên hàm của hàm số \(f(x) = 3{x^2} + 1\) là
\({x^3} + C\)
\(\frac{{{x^3}}}{3} + x + C\)
\(6x + C\)
\({x^3} + x + C\)
Nguyên hàm của hàm số \(f\left( x \right) = {x^3} + x\) là
A.\(\frac{1}{4}{x^4} + \frac{1}{2}{x^2} + C\)
\(3{x^2} + 1 + C\)
C.
\({x^3} + x + C\)
D.
\({x^4} + {x^2} + C\)
Nguyên hàm của hàm số \(f\left( x \right) = {x^3} + x\) là
\(\frac{1}{4}{x^4} + \frac{1}{2}{x^2} + C\)
\(3{x^2} + 1 + C\)
\({x^3} + x + C\)
\({x^4} + {x^2} + C\)
Nguyên hàm của hàm số \[f\left( x \right) = {x^4} + {x^2}\] là
A.\[\frac{1}{5}{x^5} + \frac{1}{3}{x^3} + C\]
\[{x^4} + {x^2} + C\]
C.
\[{x^5} + {x^3} + C\].
D.
\[4{x^3} + 2x + C\]
Nguyên hàm của hàm số \[f\left( x \right) = {x^4} + {x^2}\] là
\[\frac{1}{5}{x^5} + \frac{1}{3}{x^3} + C\]
\[{x^4} + {x^2} + C\]
\[{x^5} + {x^3} + C\].
\[4{x^3} + 2x + C\]
Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số \(y = {x^{2022}}\)?
\(\frac{{{x^{2023}}}}{{2023}} + 1\).
B.
\(\frac{{{x^{2023}}}}{{2023}}\).
C.\(y = 2022{x^{2021}}\).
D. 
.
Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số \(y = {x^{2022}}\)?
\(\frac{{{x^{2023}}}}{{2023}} + 1\).
\(\frac{{{x^{2023}}}}{{2023}}\).
\(y = 2022{x^{2021}}\).
D. 
.
Nguyên hàm của hàm số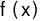 
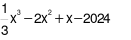là
C.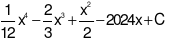
.
B.
.
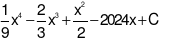D.
.
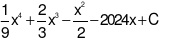Nguyên hàm của hàm số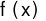 
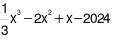là
A. 
.
B.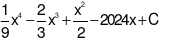 
.
C.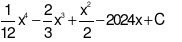 
.
D.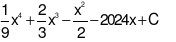 
.
Tìm nguyên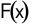 
của hàm số 
C.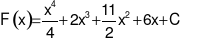
.
B.
.
D.
.
Tìm nguyên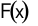 
của hàm số 
A. 
.
B. 
.
C.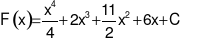 
.
D. 
.
Tìm nguyên hàm của hàm số 
.
A.
.
B.
.
D.
.
Tìm nguyên hàm của hàm số 
.
A. 
.
B. 
.
C. 
.
D. 
.
Tính 
.
B.
.
C.
.
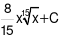D.
.
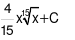Tính 
.
A. 
.
B. 
.
C.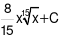 
.
D.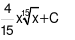 
.