30 CÂU HỎI
Cho hình phẳng \[D\] giới hạn bởi đường cong \(y = \sqrt {2 + \sin x} \), trục hoành và các đường thẳng \(x = 0\), \(x = \pi \). Khối tròn xoay tạo thành khi quay \(D\) quay quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
\(V = 2\pi \left( {\pi + 1} \right)\)
\(V = 2\pi \)
\(V = 2\left( {\pi + 1} \right)\)
V = 2
Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol \(\left( P \right):y = {x^2}\), đường thẳng \(d:y = 2x\) và đường thẳng \(x = 0,x = 2\) quay xung quanh trục \[Ox\].
\(\pi \int\limits_0^2 {{{\left( {{x^2} - 2x} \right)}^2}dx} \).
\(\pi \int\limits_0^2 {4{x^2}dx - \pi \int\limits_0^2 {{x^4}dx} } \).
\(\pi \int\limits_0^2 {4{x^2}dx + \pi \int\limits_0^2 {{x^4}dx} } \).
\(\pi \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} \)
Mệnh đề nào sau đây đúng?
\[V = \pi \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}{\rm{d}}x} \].
\[V = \int\limits_0^2 {\left( {{x^2} + 3} \right){\rm{d}}x} \].
\[V = \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}{\rm{d}}x} \].
\[V = \pi \int\limits_0^2 {\left( {{x^2} + 3} \right){\rm{d}}x} \].
Gọi \(V\) là thể tích của khối tròn xoay thu được khi quay hình thang cong, giới hạn bởi đồ thị hàm số \(y = \sin x\), trục Ox, trục Oy và đường thẳng \(x = \frac{\pi }{2}\), xung quanh trục Ox. Mệnh đề nào dưới đây đúng?
\(V = \int\limits_0^{\frac{\pi }{2}} {{{\sin }^2}xdx} \)
\(V = \int\limits_0^{\frac{\pi }{2}} {\sin xdx} \)
\(V = \pi \int\limits_0^{\frac{\pi }{2}} {{{\sin }^2}xdx} \)
\(V = \pi \int\limits_0^{\frac{\pi }{2}} {\sin xdx} \)
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị của hàm số \[y = {x^2} - 2x\], trục hoành, đường thẳng \[x = 0\] và \[x = 1\]quanh trục hoành bằng
\[\frac{{16\pi }}{{15}}\].
\[\frac{{2\pi }}{3}\].
\[\frac{{4\pi }}{3}\].
\[\frac{{8\pi }}{{15}}\].
Cho miền phẳng \(\left( D \right)\) giới hạn bởi \(y = \sqrt x \), hai đường thẳng \(x = 1\), \(x = 2\) và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay \(\left( D \right)\) quanh trục hoành.
\(3\pi \).
\(\frac{{3\pi }}{2}\).
\(\frac{{2\pi }}{3}\).
\(\frac{3}{2}\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = 2x - {x^2}\), \(y = 0\). Quay \(\left( H \right)\) quanh trục hoành tạo thành khối tròn xoay có thể tích là
\(\int\limits_0^2 {\left( {2x - {x^2}} \right)dx} \)
\(\pi \int\limits_0^2 {{{\left( {2x - {x^2}} \right)}^2}dx} \)
\(\int\limits_0^2 {{{\left( {2x - {x^2}} \right)}^2}dx} \)
\(\pi \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} \)
Cho hình phẳng giới hạn bởi các đường \[y = \sqrt x - 2\], \[y = 0\] và \[x = 4,x = 9\] quay xung quanh trục \[Ox\]. Tính thể tích khối tròn xoay tạo thành.
\[V = \frac{7}{6}\].
\[V = \frac{{5\pi }}{6}\].
\[V = \frac{{7\pi }}{{11}}\].
\[V = \frac{{11\pi }}{6}\].
Cho hình phẳng \[\left( H \right)\] giới hạn bởi các đường thẳng \(y = {x^2} + 2,y = 0,x = 1,x = 2\). Gọi \[V\] là thể tích của khối tròn xoay được tạo thành khi quay \[\left( H \right)\]xung quanh trục \[Ox\]. Mệnh đề nào dưới đây đúng?
\(V = \int\limits_1^2 {\left( {{x^2} + 2} \right){\rm{d}}x} \)
\(V = \pi \int\limits_1^2 {{{\left( {{x^2} + 2} \right)}^2}{\rm{d}}x} \)
\(V = \int\limits_1^2 {{{\left( {{x^2} + 2} \right)}^2}{\rm{d}}x} \)
\(V = \pi \int\limits_1^2 {\left( {{x^2} + 2} \right){\rm{d}}x} \)
Trường Nguyễn Văn Trỗi muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là \(2,25\)mét, chiều rộng tiếp giáp với mặt đất là \(3\) mét. Giá thuê mỗi mét vuông là \(1500000\) đồng. Vậy số tiền nhà trường phải trả là:
\(33750000\) đồng.
\(3750000\) đồng.
\(12750000\) đồng.
\(6750000\) đồng.
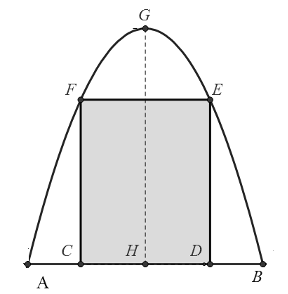
Chị Minh Hiền muốn làm một cái cổng hình Parabol như hình vẽ bên dưới. Chiều cao \(GH = 4m\), chiều rộng \(AB = 4m\), \(AC = BD = 0,9m\). Chị Minh Hiền làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm có giá là \(1200000\) đồng\(/{m^2}\), còn các phần để trắng làm xiên hoa có giá là \(900000\) đồng\(/{m^2}\). Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
\[11445000\] đồng.
\[4077000\] đồng.
\[7368000\] đồng.
\[11370000\] đồng.
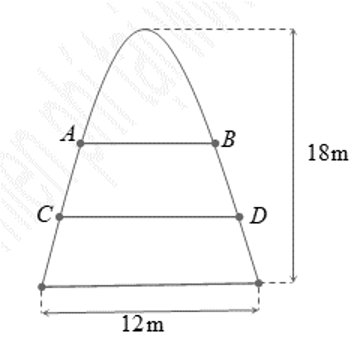
Một cổng chào có dạng hình Parabol chiều cao \[18\;{\rm{m}}\], chiều rộng chân đế \[12\;{\rm{m}}\]. Người ta căng hai sợi dây trang trí \[AB\], \[CD\] nằm ngang đồng thời chia hình giới hạn bởi Parabol và mặt đất thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số \[\frac{{AB}}{{CD}}\] bằng
\[\frac{1}{{\sqrt 2 }}\].
\[\frac{4}{5}\].
\[\frac{1}{{\sqrt[3]{2}}}\].
\[\frac{3}{{1 + 2\sqrt 2 }}\].
Một họa tiết hình cánh bướm như hình vẽ bên.
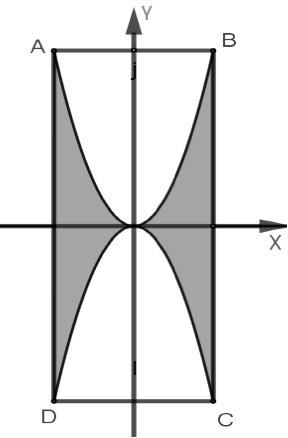
Cho \(AB = 4dm;BC = 8dm.\)Hỏi để trang trí \[1000\] họa tiết như vậy cần số tiền gần nhất với số nào sau đây.
105660667đ
1066666667đ
107665667đ
108665667đ
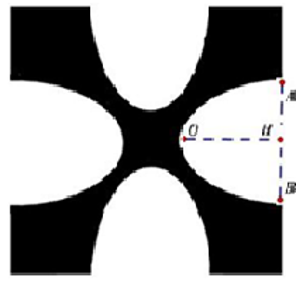
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng \[10\] cm bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết \[AB = 5\]cm, \[OH = 4\] cm. Biết giá trang trí hoa văn \[1{\rm{c}}{{\rm{m}}^2}\] là 50.000 đồng, tính số tiền cần bỏ ra để trang trí hoa văn đó.
\[2553333\] đồng.
\[2333333\] đồng.
\[2780333\] đồng.
\[2123333\] đồng.
Một viên gạch hoa hình vuông cạnh \(40{\rm{cm}}\). Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô đen như hình vẽ dưới).
Diện tích mỗi cánh hoa của viên gạch bằng
\(800\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\[\frac{{800}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
\(\frac{{400}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(250\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\) (\( - 2 \le x \le 2\)), mặt cắt là tam giác vuông có một góc \({45^0}\) và độ dài một cạnh góc vuông là \(\sqrt {14 - 3{x^2}} \) (như hình vẽ). Tính thể tích vật thể hình chiếc niêm trên.
![Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục [Ox] tại điểm có hoành độ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/anh-chup-man-hinh-2025-07-29-luc-181543-1753787697.png)
\(V = 20\)
\(V = 20\pi \)
\(V = 10\)
\(V = 10\pi \)
Trong chương trình nông thôn mới của tỉnh Phú Yên, tại xã Hòa Mỹ Tây có xây một cây cầu bằng bê tông như hình vẽ (đường cong trong hình vẽ là các đường Parabol). Biết \(1\,{{\rm{m}}^3}\) khối bê tông để đổ cây cầu có giá 5 triệu đồng. Tính số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu trên.
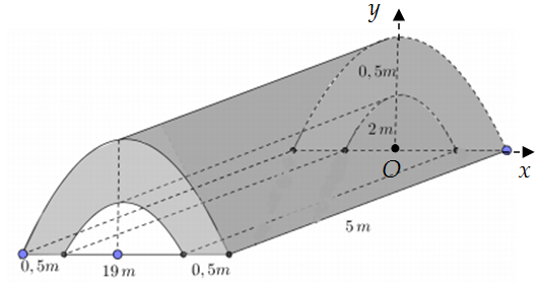
\(110\) triệu đồng.
\(250\) triệu đồng.
\(180\) triệu đồng.
\(200\) triệu đồng.
Để kỷ niệm ngày 26-3. Chi đoàn 12A dự định dựng một lều trại có dạng parabol, với kích thước: nền trại là một hình chữ nhật có chiều rộng là \(3\) mét, chiều sâu là \(6\) mét, đỉnh của parabol cách mặt đất là \(3\) mét. Hãy tính thể tích phần không gian phía bên trong trại để lớp 12A cử số lượng người tham dự trại cho phù hợp.
\(30\;{m^3}\)
\(36\;{m^3}\)
\(40\;{m^3}\)
\(41\;{m^3}\)
Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng\[R\]. Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc \[{30^0}\] ta thu được hai khối gỗ có thể tích là \[{V_1}\] và \[{V_2}\], với \[{V_1} < {V_2}\]. Thể tích \[{V_1}\] bằng?
\[{V_1} = \frac{{2\sqrt 3 {R^3}}}{9}\].
\[{V_1} = \frac{{\sqrt 3 \pi {R^3}}}{{27}}\].
\[{V_1} = \frac{{\sqrt 3 \pi {R^3}}}{{18}}\].
\[{V_1} = \frac{{\sqrt 3 {R^3}}}{{27}}\].
Cho một mô hình \[3 - D\] mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài \[5\,\left( {{\rm{cm}}} \right)\]; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức\(y = 3 - \frac{2}{5}x\) \[\left( {{\rm{cm}}} \right)\], với \(x\)\[\left( {{\rm{cm}}} \right)\] là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị\(c{m^3}\)) không gian bên trong đường hầm mô hình ( làm tròn kết quả đến hàng đơn vị)
![Cho một mô hình [3D] mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid13-1753788326.png)
\(29\).
\(27\).
\(31\).
\(33\).
Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn Minh Hiền đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \[OO' = 5\]\[{\rm{cm}}\], \[OA = 10\]\[{\rm{cm}}\], \[OB = 20\] \[{\rm{cm}}\], đường cong \[AB\] là một phần của parabol có đỉnh là điểm\[A\]. Thể tích của chiếc mũ bằng
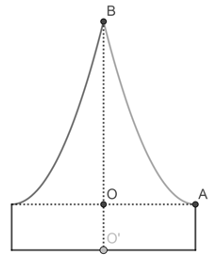
\(\frac{{2750\pi }}{3}\) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
\(\frac{{2500\pi }}{3}\) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
\(\frac{{2050\pi }}{3}\)\(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
\(\frac{{2250\pi }}{3}\) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Một chi tiết máy được thiết kế như hình vẽ bên.
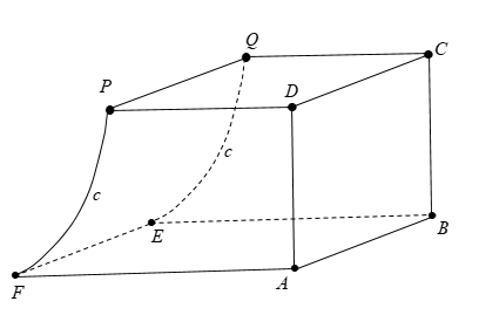Các tứ giác \(ABCD,CDPQ\) là các hình vuông cạnh \(2,5\,cm\). Tứ giác \(ABEF\) là hình chữ nhật có \(BE = 3,5\,cm\). Mặt bên\(PQEF\)được mài nhẵn theo đường parabol \(\left( P \right)\) có đỉnh parabol nằm trên cạnh \(EF\). Thể tích của chi tiết máy bằng
\(\frac{{395}}{{24}}\,c{m^3}\).
\(\frac{{50}}{3}\,\,c{m^3}\).
\(\frac{{125}}{8}\,c{m^3}\).
\(\frac{{425}}{{24}}\,c{m^3}\).
Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn \(28\,{\rm{cm}}\), trục nhỏ \(25\,{\rm{cm}}\). Biết cứ \(1000\,{\rm{c}}{{\rm{m}}^3}\) dưa hấu sẽ làm được cốc sinh tố giá \(20000\) đồng. Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
\(183000\) đồng.
\(180000\) đồng.
\(185000\) đồng.
\(190000\) đồng.
Một cốc rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bổ dọc cốc thành 2 phần bằng nhau) là một đường Parabol. Tính thể tích tối đa mà cốc có thể chứa được (làm tròn 2 chữ số thập phân)
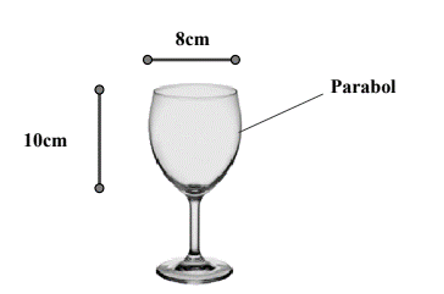
\(V \approx 320c{m^3}\).
\(V \approx 1005,31c{m^3}\).
\(V \approx 251,33c{m^3}\).
\(V \approx 502,65c{m^3}\).
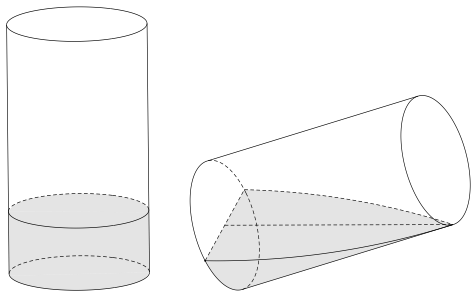
Có một cốc nước thủy tinh hình trụ, bán kính trong lòng đáy cốc là \(6\,{\rm{cm}}\), chiều cao lòng cốc là \(10\,{\rm{cm}}\) đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiêng cốc nước vừa lúc khi nước chạm miệng cốc thì đáy mực nước trùng với đường kính đáy.
\(240\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
\(240\pi \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
\(120\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
\(120\pi \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
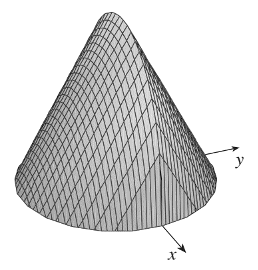
Cho vật thể đáy là hình tròn có bán kính bằng 1 (tham khảo hình vẽ). Khi cắt vật thể bằng mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\;\left( { - 1 \le x \le 1} \right)\) thì được thiết diện là một tam giác đều. Thể tích \(V\) của vật thể đó là
\[V = \sqrt 3 \].
\[V = 3\sqrt 3 \].
\[V = \frac{{4\sqrt 3 }}{3}\].
\[V = \pi \].
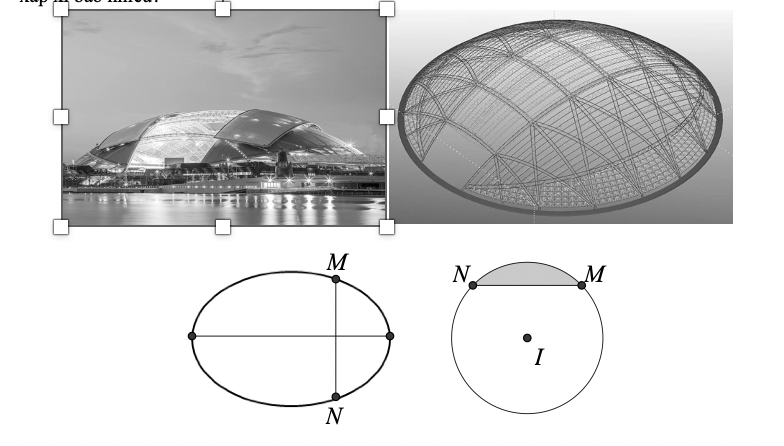
Sân vận động Sport Hub (Singapore) là sân có mái vòm kỳ vĩ nhất thế giới. Đây là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á được tổ chức tại Singapore năm \[2015\]. Nền sân là một elip \(\left( E \right)\) có trục lớn dài \[150m\], trục bé dài \[90m\] (hình vẽ). Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của \(\left( E \right)\)và cắt elip ở \(M,N\) (hình vẽ) thì ta được thiết diện luôn là một phần của hình tròn có tâm \(I\) (phần tô đậm trong hình 4) với \(MN\) là một dây cung và góc \(\widehat {MIN} = {90^0}.\) Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Hỏi thể tích xấp xỉ bao nhiêu?
\(57793{m^3}\).
\(115586{m^3}\).
\(32162{m^3}\).
\(101793{m^3}\).
Gọi \(\left( H \right)\) là phần giao của hai khối \(\frac{1}{4}\) hình trụ có bán kính \(a\), hai trục hình trụ vuông góc với nhau như hình vẽ sau. Tính thể tích của khối \(\left( H \right)\).
\({V_{\left( H \right)}} = \frac{{{a^3}}}{2}\).
\({V_{\left( H \right)}} = \frac{{3{a^3}}}{4}\).
\({V_{\left( H \right)}} = \frac{{2{a^3}}}{3}\).
\({V_{\left( H \right)}} = \frac{{\pi {a^3}}}{4}\).
Một bác thợ xây bơm nước vào bể chứa nước. Gọi \[h\left( t \right)\] là thể tích nước bơm được sau \[t\] giây. Cho \[h'\left( t \right) = 6a{t^2} + 2bt\] và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là \[90{m^3}\], sau \[6\] giây thì thể tích nước trong bể là \[504{m^3}\]. Tính thể tích nước trong bể sau khi bơm được \[9\] giây.
\[1458{m^3}\].
\[600{m^3}\].
\[2200{m^3}\].
\[4200{m^3}.\]
Người ta thay nước mới cho một bể bơi có dạng hình hộp chữ nhật có độ sâu là \(280\)cm. Giả sử \(h\left( t \right)\)là chiều cao (tính bằng cm) của mực nước bơm được tại thời điểm \(t\) giây, biết rằng tốc độ tăng của chiều cao mực nước tại giây thứ \(t\) là \(h'(t) = \frac{1}{{500}}\sqrt[3]{t}\) và lúc đầu hồ bơi không có nước. Hỏi sau bao lâu thì bơm được số nước bằng \(\frac{3}{4}\)độ sâu của hồ bơi (làm tròn đến giây)?
\(2\) giờ \(36\) giây.
\(2\) giờ \(48\) giây.
\(2\) giờ \(38\) giây.
\(2\) giờ \(46\) giây.