26 câu hỏi
Cho hai hàm số \(f(x)\) và \(g(x)\) liên tục trên \(\left[ {a\,;\,b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = f(x)\), \(y = g(x)\) và các đường thẳng \(x = a\), \(x = b\) bằng
\(\left| {\int\limits_a^b {\left[ {f(x) - g(x)} \right]{\rm{d}}x} } \right|\).
\(\int\limits_a^b {\left| {f(x) + g(x)} \right|{\rm{d}}x} \).
\(\int\limits_a^b {\left| {f(x) - g(x)} \right|{\rm{d}}x} \).
\(\int\limits_a^b {\left[ {f(x) - g(x)} \right]{\rm{d}}x} \).
Gọi \(S\) là diện tích của hình phẳng giới hạn bởi các đường \(y = {3^x}\), \(y = 0\),\(x = 0\),\(x = 2\). Mệnh đề nào dưới đây đúng?
\(S = \int\limits_0^2 {{3^x}} dx\)
\(S = \pi \int\limits_0^2 {{3^{2x}}} dx\).
\(S = \pi \int\limits_0^2 {{3^x}} dx\).
\(S = \int\limits_0^2 {{3^{2x}}} dx\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\left( {x - 2} \right)^2} - 1\), trục hoành và hai đường thẳng \(x = 1,\,x = 2\) bằng
\(\frac{2}{3}\).
\(\frac{3}{2}\).
\(\frac{1}{3}\).
\(\frac{7}{3}\).
Tính diện tích \(S\) hình phẳng giới hạn bởi các đường \(y = {x^2} + 1,\,x = - 1,\,x = 2\) và trục hoành.
\(S = 6\).
\(S = 16\).
\(S = \frac{{13}}{6}\).
\(S = 13\).
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} + 5\),\(y = 6x\), \(x = 0\),\(x = 1\). Tính \(S\).
\(\frac{4}{3}\)
\(\frac{7}{3}\)
\(\frac{8}{3}\)
\(\frac{5}{3}\)
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = \ln x,\] \[y = 1\] và hai đường thẳng \[x = 1,x = e\] bằng
\({e^2}\).
\[e + 2\].
\[2e\].
\[e - 2\].
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 4x - {x^2}\), \(y = 2x\) và hai đường thẳng \[x = 1,x = e\] bằng
\(4\).
\(\frac{{20}}{3}\).
\(\frac{4}{3}\).
\(\frac{{16}}{3}\)
Tính diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = {x^2} - 2x\), \(y = 0\), \(x = - 10\), \(x = 10\).
\[S = \frac{{2000}}{3}\].
\(S = 2008\).
\[S = 2000\].
\(S = \frac{{2008}}{3}\).
Gọi \[S\] là diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục hoành, đường thẳng \[x = a,x = b\] (như hình vẽ bên). Hỏi cách tính \[S\] nào dưới đây đúng?
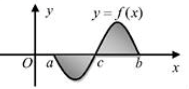
\(S = \int\limits_a^b {f\left( x \right)dx} \).
\(S = \left| {\int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} } \right|\).
\(S = - \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \).
\[S = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \].
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \[\left[ {a;b} \right]\]. Gọi \[D\] là diện tích hình phẳng giới hạn bởi đồ thị \[\left( C \right):y = f\left( x \right)\], trục hoành, hai đường thẳng \[x = a\], \[x = b\] (như hình vẽ dưới đây). Giả sử \[{S_D}\] là diện tích hình phẳng \[D\]. đúng trong các phương án A, B, C, D cho dưới đây?
![Cho hàm số y = f( x ) liên tục trên đoạn [a;b]. Gọi [D] là diện tích hình phẳng giới hạn bởi đồ thị ( C):y = f( x ), trục hoành, (ảnh 1)](https://video.vietjack.com/upload2/images/1753777506/1753777575-image3.png)
\({S_D} = \int\limits_a^0 {f\left( x \right){\rm{d}}x} + \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
\({S_D} = - \int\limits_a^0 {f\left( x \right){\rm{d}}x} + \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
\({S_D} = \int\limits_a^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
\({S_D} = - \int\limits_a^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục hoành và hai đường thẳng \[x = a\], \[x = b\]\[\left( {a < b} \right)\] (phần tô đậm trong hình vẽ) tính theo công thức nào dưới đây ?</>
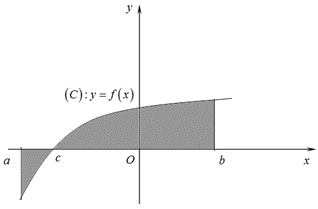
\(S = \int\limits_a^c {f\left( x \right){\rm{d}}x + \int\limits_c^b {f\left( x \right){\rm{d}}x} } \).
\[S = \int\limits_a^b {f\left( x \right){\rm{d}}x} \].
\(S = - \int\limits_a^c {f\left( x \right){\rm{d}}x + \int\limits_c^b {f\left( x \right){\rm{d}}x} } \).
\[S = \left| {\int\limits_a^b {f\left( x \right){\rm{d}}x} } \right|\].
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
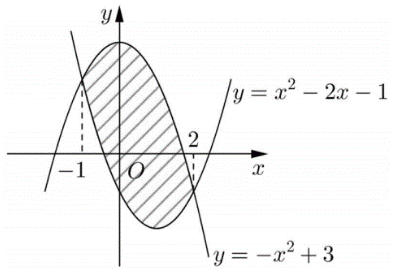
\(\int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx} \)
\(\int\limits_{ - 1}^2 {\left( {2x - 2} \right)dx} \)
\(\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \)D. \(\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \)
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}.\) Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 5\) (như hình vẽ bên).
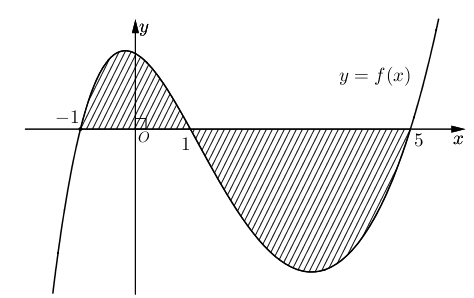
Mệnh đề nào sau đây đúng?
\[S = - \int\limits_{ - 1}^1 {f(x){\rm{d}}x - } \int\limits_1^5 {f(x){\rm{d}}x} \].
\[S = \int\limits_{ - 1}^1 {f(x){\rm{d}}x + } \int\limits_1^5 {f(x){\rm{d}}x} \].
\[S = \int\limits_{ - 1}^1 {f(x){\rm{d}}x - } \int\limits_1^5 {f(x){\rm{d}}x} \].
\[S = - \int\limits_{ - 1}^1 {f(x){\rm{d}}x + } \int\limits_1^5 {f(x){\rm{d}}x} \].
Cho hàm số \[f\left( x \right)\] liên tục trên \[\mathbb{R}\]. Gọi S là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right),y = 0,x = - 1,x = 2\] (như hình vẽ bên). Mệnh đề nào dưới đây đúng?
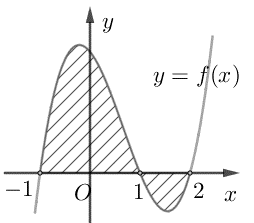
\[S = \int\limits_{ - 1}^1 {f\left( x \right)} {\rm{ dx + }}\int\limits_1^2 {f\left( x \right)} {\rm{ dx}}\].
\[S = - \int\limits_{ - 1}^1 {f\left( x \right)} {\rm{ dx}} - \int\limits_1^2 {f\left( x \right)} {\rm{ dx}}\].
\[S = - \int\limits_{ - 1}^1 {f\left( x \right)} {\rm{ dx + }}\int\limits_1^2 {f\left( x \right)} {\rm{ dx}}\].
\[S = \int\limits_{ - 1}^1 {f\left( x \right)} {\rm{ dx }} - \int\limits_1^2 {f\left( x \right)} {\rm{ dx}}\].
Gọi\(S\)là diện tích hình phẳng \(\left( H \right)\)giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 1\), \(x = 2\). Đặt \(a = \int\limits_{ - 1}^0 {f\left( x \right){\rm{d}}x} \),\(b = \int\limits_0^2 {f\left( x \right){\rm{d}}x} \), mệnh đề nào sau đây đúng?
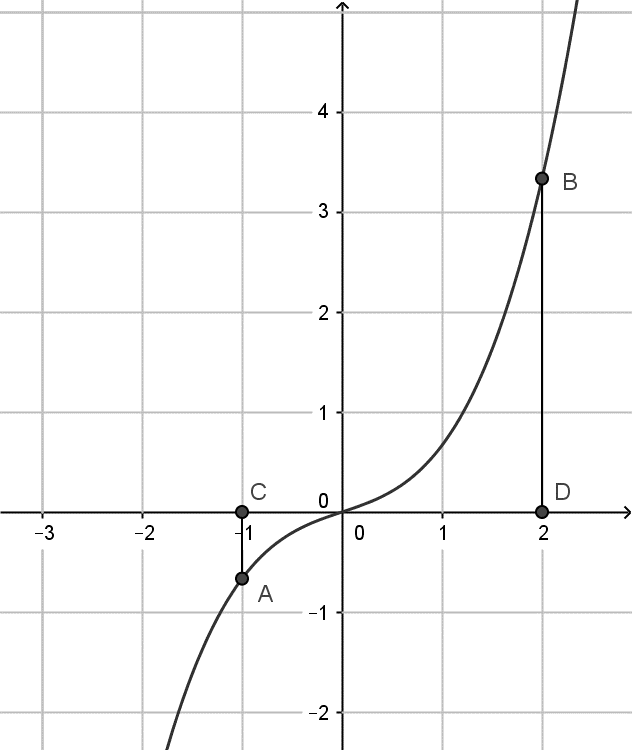
\(S = b - a\)
\(S = b + a\)
\(S = - b + a\)
\(S = - b - a\)
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 3\), \(x = 2\) (như hình vẽ bên). Đặt \(a = \int\limits_{ - 3}^1 {f\left( x \right)\,{\rm{d}}x} \), \(b = \int\limits_1^2 {f\left( x \right)\,{\rm{d}}x} \). Mệnh đề nào sau đây là đúng.
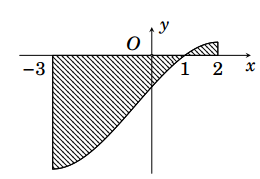
\(S = a + b\).
\(S = a - b\).
\(S = - a - b\).
\(S = b - a\).
Diện tích phần hình phẳng được tô đậm trong hình vẽ bên được tính theo công thức nào dưới đây?
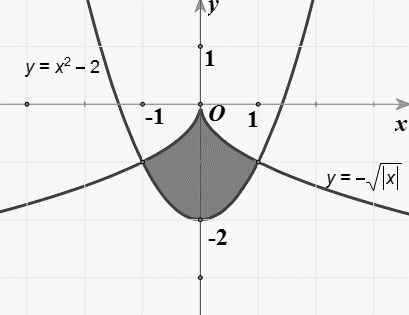
\[\int\limits_{ - 1}^1 {\left( {{x^2} - 2 + \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
\[\int\limits_{ - 1}^1 {\left( {{x^2} - 2 - \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
\[\int\limits_{ - 1}^1 {\left( { - {x^2} + 2 + \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
\[\int\limits_{ - 1}^1 {\left( { - {x^2} + 2 - \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
Viết công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), xung quanh trục \(Ox\).</>
\(V = \int\limits_a^b {\left| {f\left( x \right)} \right|} dx\)
\(V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx\)
\(V = \int\limits_a^b {{f^2}\left( x \right)} dx\)
\(V = \pi \int\limits_a^b {f\left( x \right)} dx\)
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục \[Ox\] tại \(x = 1\) và \(x = 2\). Một mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\) (\(1 \le x \le 2\)) cắt vật thể đó có diện tích \(S\left( x \right) = 2024x\). Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên.
\(V = 3036\)
\(V = 3036\pi \)
\(V = 1518\)
\(V = 1518\pi \)
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục \[Ox\] tại \(x = 1\) và \(x = 3\). Một mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \(x\) (\(1 \le x \le 3\)) cắt vật thể đó theo thiết diện là một hình chữ nhật có độ dài hai cạnh là \(3x\) và \(3{x^2} - 2\). Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên.
\(V = 156\)
\(V = 156\pi \)
\(V = 312\)
\(V = 312\pi \)
Gọi \(D\) là hình phẳng giới hạn bởi các đường \(y = {e^{3x}}\), \(y = 0\), \(x = 0\) và \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) bằng:
\(\pi \int\limits_0^1 {{e^{3x}}dx} \).
\(\int\limits_0^1 {{e^{6x}}dx} \).
\(\pi \int\limits_0^1 {{e^{6x}}dx} \).
\(\int\limits_0^1 {{e^{3x}}dx} \).
Gọi \(D\) là hình phẳng giới hạn bởi các đường \(y = {e^{4x}},y = 0,x = 0\) và \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) bằng
\(\int\limits_0^1 {{e^{4x}}{\rm{d}}x} \).
\(\pi \int\limits_0^1 {{e^{8x}}{\rm{d}}x} \).
\(\pi \int\limits_0^1 {{e^{4x}}{\rm{d}}x} \).
\(\int\limits_0^1 {{e^{8x}}{\rm{d}}x} \).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = {x^2} + 3\), \(y = 0\), \(x = 0\), \(x = 2\). Gọi \(V\) là thể tích của khối tròn xoay được tạo thành khi quay \(\left( H \right)\) xung quanh trục \(Ox\). Mệnh đề nào dưới đây đúng?
\(V = \int\limits_0^2 {\left( {{x^2} + 3} \right)dx} \)
\(V = \pi \int\limits_0^2 {\left( {{x^2} + 3} \right)dx} \)
\(V = \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}dx} \)
\(V = \pi \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}dx} \)
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = {e^x}\), trục hoành và các đường thẳng \(x = 0\), \(x = 1\). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
\(V = \frac{{\pi \left( {{e^2} + 1} \right)}}{2}\)
\(V = \frac{{{e^2} - 1}}{2}\)
\(V = \frac{{\pi {e^2}}}{3}\)
\(V = \frac{{\pi \left( {{e^2} - 1} \right)}}{2}\)
Cho hình phẳng \(D\) giới hạn với đường cong \(y = \sqrt {{x^2} + 1} \), trục hoành và các đường thẳng \(x = 0,x = 1\). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
\(V = 2\)
\(V = \frac{{4\pi }}{3}\)
\(V = 2\pi \)
\(V = \frac{4}{3}\)
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = \sqrt {2 + \cos x} ,\) trục hoành và các đường thẳng \(x = 0,x = \frac{\pi }{2}\). Khối tròn xoay tạo thành khi \(D\) quay quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
\(V = (\pi + 1)\pi \)
\(V = \pi - 1\)
\(V = \pi + 1\)
\(V = (\pi - 1)\pi \)
