30 câu hỏi
Đường đi trong đồ thị G vô hướng từ đỉnh s đến đỉnh t là một dãy:
Các cạnh e1,e2,…,en kề nhau
Các đỉnh v0 = s, v1, v2, …,vn = t kề nhau, các cạnh ei=(vi-1,vi) đôi một khác nhau, i = 0..n.
Các cạnh e1,e2,…,en không kề nhau.
Các đỉnh v0 = s, v1, v2, …,vn = t không kề nhau
Cho đồ thị v × G vô hướng, đỉnh có bậc bằng 1 khi:
Có một cạnh xuất phát từ v
Có hơn một cạnh xuất phát từ v
Có đúng một cạnh đi vào và có hơn một đỉnh đi ra khỏi đỉnh này.
Tồn tại khuyên ở đỉnh đó.
Đồ thị G là không liên thông nếu nó chứa:
Cạnh có hướng
Đỉnh cô lập
Đỉnh treo.
Cạnh vô hướng
Đồ thị G vô hướng được gọi là liên thông nếu giữa mọi cặp đỉnh u,v bất kỳ đều có:
Một cạnh nối giữa u và v
Một đường đi có hướng nối u đến v
Một đường đi vô hướng nối u đến v
Hai cạnh nối u đến v
Chu trình trên đồ thị G là:
Đường đi có hướng với đỉnh đầu và đỉnh cuối trùng nhau.
Đường đi có đỉnh đầu và đỉnh cuối trùng nhau.
Đường đi có đỉnh đầu và đỉnh cuối kề nhau.
Đường đi có đỉnh đầu và đỉnh cuối không kề nhau
Số đỉnh bậc lẻ trong đồ thị G vô hướng:
Phụ thuộc vào số đỉnh của đồ thị.
Là một số lẻ
Là một số chẵn.
Phụ thuộc vào số cạnh của đồ thị.
Chu trình đơn trên đồ thị G là:
Đường đi đơn có đỉnh đầu và đỉnh cuối trùng nhau.
Đường đi có hướng với đỉnh đầu và đỉnh cuối trùng nhau.
Đường đi đơn có đỉnh đầu và đỉnh cuối kề nhau.
Đường đi có đỉnh đầu và đỉnh cuối khác nhau
Bậc của đỉnh trong đồ thị có hướng G là:
Số cạnh đi vào đỉnh đó.
Số cạnh đi ra khỏi đỉnh đó.
Tổng của cạnh đi vào và số cạnh đi ra khỏi đỉnh đó.
Hiệu của cạnh đi vào và cạnh đi ra khỏi đỉnh đó
Độ dài của một chu trình trên đồ thị G là:
Số cạnh tạo thành chu trình.
Số đỉnh tạo thành chu trình +1.
Số cạnh tạo chu trình + 1.
Số đỉnh trên tạo chu trình – 1.
Đỉnh cô lập trên đồ thị G là:
Đỉnh có 2 đỉnh kề với nó.
Đỉnh có bậc bằng 1
Đỉnh có bậc bằng 0
Đỉnh có bậc -1
Đường đi đơn trong đồ thị G là đường đi:
Các đỉnh trên nó đối xứng từng đôi một
Các đỉnh chỉ xuất hiện một lần trừ đỉnh đầu và đỉnh cuối.
Đỉnh đầu và đỉnh cuối khác nhau.
Mỗi đỉnh chỉ kề với hai đỉnh.
Đồ thị đầy đủ K có số đỉnh và số cạnh tương ứng là:
n, 2n.
n, n(2n-1)/2.
n+1, 2n.
n, n(n-1)/2.
Đồ thị C có số đỉnh và số cạnh tương ứng là:
n, n+1
n, n
n, n-1
n, 2n
Đồ thị lập phương Qn là đồ thị:
chỉ khác nhau một bit
2n đỉnh, mỗi đỉnh kề nhau chỉ khác nhau một bit.
2n đỉnh, mỗi đỉnh kề nhau chỉ khác nhau nhiều nhất 2 bit.
2n đỉnh, mỗi đỉnh được biểu diễn bởi một xâu bit độ dài n sao cho hai đỉnh kề nhau
n đỉnh, mỗi đỉnh được biểu diễn bởi một xâu bit độ dài n sao cho hai đỉnh kề nhau chỉ khác nhau một bit.
Chu trình Euler của đồ thị là chu trình đi qua tất cả các đỉnh.
Mỗi đỉnh đúng một lần.
Mỗi cạnh đúng một lần.
Mỗi cạnh không quá một lần
Đi qua đỉnh đầu và đỉnh cuối hai lần
Chu trình Euler đi qua mỗi đỉnh của đồ thị:
Không quá một lần
Đúng một lần.
Không xác định
Nhiều hơn một lần
Đường đi Euler đi qua mỗi cạnh của đồ thị:
Không quá một lần.
Đúng một lần.
Không xác định
Có thể nhiều hơn một lần.
Chu trình Hamilton là chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh.
Không quá một lần.
Đúng một lần.
Luôn nhiều hơn một lần.
Không xác định
Đường đi Hamilton là đường đi đi qua tất cả các đỉnh của đồ thị mỗi đỉnh.
Đúng một lần
Luôn nhiều hơn một lần.
Không quá một lần.
Không xác định.
Đồ thị G được gọi là nửa Hamilton nếu tồn tại đường đi đi qua tất cả các đỉnh của đồ thị.
Mỗi cạnh một lần.
Mỗi cạnh không quá một lần.
Mỗi đỉnh một lần.
Một đỉnh không quá một lần.
Đa đồ thị liên thông G có chu trình Hamilton nếu:
Bậc của các đỉnh trong đồ thị -2
Bậc của các đỉnh trong đồ thị -n
Bậc của các đỉnh trong đồ thị -n/2
Bậc của các đỉnh trong đồ thị -n/4
Một đồ thị được gọi là phẳng nếu:
Có thể vẽ được trên một mặt phẳng mà có các cạnh cắt nhau ở đỉnh ngoài
Có thể vẽ được trên một mặt phẳng mà không có các cạnh nào cắt nhau
Có thể vẽ được trên một mặt phẳng mà có hai cạnh bất kỳ cắt nhau
Có thể vẽ được trên một mặt phẳng mà không có quá hai cạnh cắt nhau
Số màu của một đồ thị là:
Số trung bình các màu cần thiết để tô màu đồ thị này
Số tối thiểu các màu cần thiết để tô màu đồ thị này
Số tối đa các màu cần thiết để tô màu đồ thị này
Số theo yêu cầu các màu cần thiết để tô màu đồ thị này
Số màu của một đồ thị phẳng là:
Bằng 5.
Lớn hơn 4.
Lớn hơn hoặc bằng 5.
Không lớn hơn 4
Đồ thị đầy đủ Kn có số màu bằng:
(n- 2)
n
(n-1)
n(n-1)/2
Đồ thị G vô hướng n đỉnh là một cây nếu:
Nếu liên thông và có n-1 cạnh
Nếu không liên thông và có n-1 cạnh
Nếu liên thông và có n cạnh
Nếu không liên thông và có n cạnh
Cây là một đồ thị vô hướng:
Liên thông và số đỉnh nhỏ hơn số cạnh là 1.
Liên thông và số đỉnh bằng số cạnh
Liên thông và không chứa chu trình
Không liên thông và có số đỉnh bằng số cạnh là 1.
Bài toàn xây dựng cây khung nhỏ nhất của đồ thị được phát biểu trên:
Đồ thị có hướng có trọng số B. Đồ thị vô hướng có trọng số bất kỳ C. Đồ thị vô hướng D. Đồ thị vô hướng có trọng số dương
Cho G =(V,E) là đồ thị vô hướng liên thông n đỉnh. Cây T =(VT , ET ) được gọi là cây khung của đồ thị G nếu:
T liên thông và mỗi cạnh của nó đều là cầu.
Nếu thêm vào T một cạnh thì ta có ít nhất một chu trình
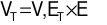
T liên thông, có đúng n cạnh và 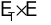
Cho G =(V,E) là đồ thị vô hướng liên thông n đỉnh. T = (VT , ET ) được gọi là cây khung của đồ thị G nếu:
T liên thông và chứa n đỉnh của G.
T không liên thông, không chứa chu trình và chứa n cạnh của G.
T liên thông, không chứa chu trình và chứa n đỉnh của G.
