30 câu hỏi
Một học viên phải trả lời 8 trong số 10 câu hỏi cho một kỳ thi. Học viên này có bao nhiêu sự lựa chọn nếu học viên phải trả lời ít nhất 4 trong 5 câu hỏi đầu tiên?
75
35
45
30
Có 12 học viên trong một lớp. Có bao nhiêu cách để 12 học viên có 3 bài kiểm tra khác nhau nếu 4 học viên có chung mỗi bài kiểm tra?
34650
220
3465
650
Nếu G = (V,E) là một đồ thị vô hướng thì:
Số đỉnh bậc lẻ và số đỉnh bậc chẵn là một số chẵn
Số đỉnh bậc chẵn là một số chẵn
Số đỉnh bậc lẻ là một số chẵn
Số đỉnh bậc lẻ là một số lẻ
Những đơn đồ thị vô hướng nào dưới đây tồn tại nếu bậc của các đỉnh lần lượt là:
1, 4, 3, 2, 5, 6.
2, 1, 5, 2, 3, 3.
2, 4, 3, 4, 3, 2.
1, 4, 3, 2, 2, 3.
Đơn đồ thị vô hướng nào dưới đây tồn tại nếu bậc của các đỉnh lần lượt là:
1, 2, 3, 4, 5.
0, 1, 2, 2, 3.
3, 4, 3, 4, 3.
1, 2, 3, 4, 7.
Đồ thị liên thông nào trong các đồ thị dưới đây là đồ thị Euler nếu số bậc của các đỉnh lần lượt là:
2, 4, 1, 2, 6
3, 4, 4, 2, 4
1, 4, 2, 5, 2
4, 4, 6, 5, 3
Trong cách biểu diễn đồ thị bằng danh sách cạnh chúng ta lưu trữ:
Danh sách tất cả các cạnh.
Danh sách tất cả các đỉnh
Danh sách tất cả các cạnh và các đỉnh.
Không lưu trữ danh sách cạnh và đỉnh nào.
Trong biểu diễn đồ thị bằng danh sách kề, mỗi danh sách kề chứa:
Các cạnh kề với một đỉnh.
Các đỉnh kề với một đỉnh.
Tất cả các đỉnh kề và cạnh kề với nó.
Các bậc của đỉnh kề với một đỉnh.
Tổng tất cả các bậc trong một đồ thị vô hướng bằng:
Hai lần số cạnh.
Hai lần số đỉnh.
Trung bình cộng của số đỉnh và số cạnh.
Tổng của số đỉnh và số cạnh.
Nếu bậc của mỗi đỉnh trong đồ thị đều chẵn thì:
Đồ thị là liên thông.
Đồ thị không liên thông.
Tính liên thông của đồ thị không xác định.
Đồ thị là liên thông mạnh
Đồ thị dưới dạng ma trận kề:
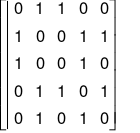
Là đồ thị:
Euler
Hamilton và Euler
Hamilton
Không liên thông
Cho đồ thị vô hướng G = (V,E), khẳng định nào sau đây là đúng?
Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần liên thông với đỉnh u
Thuật toán DFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ thị
Thuật toán DFS(u) duyệt tất cả các thành phần liên thông của đồ thị
Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
Cho đồ thị vô hướng G = (V,E), khẳng định nào dưới đây là đúng?
Thuật toán BFS(u) duyệt tất cả các thành phần liên thông của đồ thị
Thuật toán BFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ thị
Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần liên thông với đỉnh u
Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
Đồ thị K4 có số đỉnh và số cạnh tương ứng là?
4,6
4,8
5,8
4,4
Phát biểu nào sau đây là sai khi nói đến đồ thị phân đôi đầy đủ Km,n .
Có tập đỉnh được phân thành hai tập con tương ứng có m đỉnh và n đỉnh.
Có một cạnh giữa hai đỉnh nếu và chỉ nếu một đỉnh thuộc tập con này và đỉnh thứ hai thuộc tập con kia.
Có một cạnh giữa hai đỉnh nếu và chỉ nếu mỗi đỉnh đều thuộc vào hai tập đỉnh con.
Có m+n đỉnh, mn cạnh.
Đồ thị có đường đi vô hướng Euler khi và chỉ khi:
Liên thông và có hai đỉnh bậc lẻ.
Không liên thông và có hai đỉnh bậc lẻ.
Liên thông và có một đỉnh bậc lẻ.
Không liên thông và không có đỉnh bậc lẻ.
Đồ thị phân đôi đầy đủ K có số màu bằng:
3
4
2
-2
Đường đi Euler vô hướng trên một đồ thị có đỉnh đầu và đỉnh cuối:
Trùng nhau
Khác nhau
Có cùng bậc chẵn
Đỉnh đầu bậc chẵn đỉnh cuối bậc lẻ
Nếu G là đồ thị Euler thì:
Không có đỉnh bậc chẵn
Không có đường đi Euler.
Không có chu trình Euler
Có chu trình Euler
Số màu của đồ thị Cn (với n chẵn) là:
1
2
3
4
Số màu của đồ thị Cn (với n lẻ) là:
1
2
3
4
Chu trình Hamilton là:
Chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc lẻ
Chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc chẵn
Chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
Chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh hơn một lần
Đồ thị liên thông G có một đỉnh có bậc bằng một thì:
G có chu trình Hamilton
G có chu trình Euler
G không có chu trình Hamilton
G không có chu trình
Khi xây dựng chu trình Hamilton, nếu lấy hai cạnh liên thuộc với một đỉnh đặt vào chu trình thì:
Có thể xóa tất cả các cạnh còn lại không liên thuộc với đỉnh đó.
Có thể xóa tất cả các cạnh còn lại liên thuộc với đỉnh đó.
Có thể xóa tất cả các cạnh còn lại của đồ thị.
Có thể lấy thêm các cạnh liên thuộc với đỉnh đó.
Số màu trong đồ thị hình bánh xe W (với n chẵn) là:
1
2
3
4
Số màu trong đồ thị hình bánh xe Wn (với n lẻ) là:
1
2
3
4
Cho đơn đồ thị phẳng liên thông có số đỉnh bằng 6 và mỗi đỉnh đều bậc 4. Số miền trong biểu diễn phẳng của đồ thị là:
5 miền
6 miền
7 miền
8 miền
Đồ thị nào trong các đồ thị không phẳng sau đây có tính chất: bỏ đi một đỉnh bất kỳ và các cạnh liên thuộc với nó tạo ra một đồ thị phẳng.
K5
K2
K6
K7
Độ phức tạp của thật toán Floyd là:
O(n3 log2n)
O(n2)
O(n3)
O(n2 log2n)
Thuật toán Dijkstra được áp dụng cho:
Đồ thị vô hướng hoặc có hướng có trọng số không âm.
Đồ thị liên thông có trọng số không âm
Đồ thị có hướng có trọng số không âm.
Đồ thị vô hướng hoặc có hướng không có chu trình âm
