25 CÂU HỎI
Một bánh mài đang quay với vận tốc 300 vòng/phút thì bị ngắt điện và nó quay chậm dần đều. Sau đó một phút, vận tốc còn 180vòng/phút. Tính gia tốc góc.
A. \[ - \frac{\pi }{5}{\rm{rad/}}{{\rm{s}}^2}\]
B. \[ - \frac{{{\rm{2\pi }}}}{{\rm{5}}}{\rm{rad/}}{{\rm{s}}^{\rm{2}}}\]
C. \[ - \frac{{\rm{\pi }}}{{{\rm{15}}}}{\rm{rad/}}{{\rm{s}}^{\rm{2}}}\]
D. \[ - 4{\rm{\pi }}\,{\rm{rad/}}{{\rm{s}}^{\rm{2}}}\]
Một bánh mài đang quay với vận tốc 300 vòng/phút thì bị ngắt điện và nó quay chậm dần đều. Sau đó một phút, vận tốc còn 180vòng/phút. Tính số vòng nó đã quay trong thời gian đó.
A. 120 vòng
B. 240 vòng
C. 60 vòng
D. 180 vòng
Một môtơ bắt đầu khởi động nhanh dần đều, sau 2 giây đạt tốc độ ổn định 300 vòng/phút. Tính gia tốc góc của môtơ.
A. 5π rad/s2
B. 10π rad/s2
C. 15π rad/s2
D. 20π rad/s2
Một môtơ bắt đầu khởi động nhanh dần đều, sau 2 giây đạt tốc độ ổn định 300 vòng/phút. Tính góc quay của môtơ trong thời gian đó.
A. 10π rad
B. 5π rad
C. 15π rad
D. 20π rad
Một đồng hồ có kim giờ dài 3cm, kim phút dài 4cm. Gọi ωP, ωg là vận tốc góc và vp, vg là vận tốc dài của đầu kim phút, kim giờ. Quan hệ nào sau đây là đúng?
A. ωp = 12ωg; vp = 16vg
B. ωg = 12ωp ; vp = 16vg
C. ωp = 12ωg; vg = 16vp
D. ωg = 12ωp ; vg = 9vp
Một đồng hồ có kim phút và kim giờ. Phát biểu nào sau đây là đúng:
A. Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 12 lần
B. Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 24 lần
C. Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 23 lần
D. Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 22 lần
Trái đất quay quanh trục của nó với chu kỳ T = 24 giờ. Bán kính trái đất là R = 6400km. Tính vật tốc dài của một điểm ở vĩ độ 60o trên mặt đất.
A. 234 m/s
B. 467 m/s
C. 404 m/s
D. 508 m/s
Nhờ xích (sên) xe đạp mà chuyển động của đĩa được truyền tới líp xe. Giả sử ta đạp xe một cách đều đặn thì líp đĩa có cùng:
A. Vận tốc góc ω
B. Gia tốc góc β
C. Gia tốc tiếp tuyến at của các răng
D. Vận tốc dài v của các răng
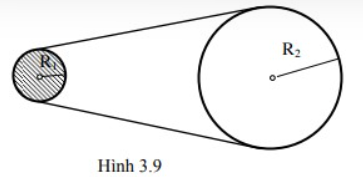
Một dây cuaroa truyền động, vòng qua vô lăng I và bánh xe II (hình 3.9). Bán kính của vô lăng và bánh xe là R1 = 10cm và R2 = 50cm. Vô lăng đang quay với vận tốc 720 vòng/phút thì bị ngắt điện, nó quay chậm dần đều, sau đó 30 giây vận tốc chỉ còn 180 vòng/phút. Vận tốc quay của bánh xe ngay trước khi ngắt điện là:
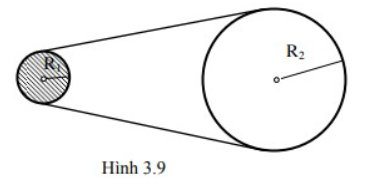
A. 720 vòng/phút
B. 144 vòng/phút
C. 3600 vòng/phút
D. 180 vòng/phút
Một dây cuaroa truyền động, vòng qua vô lăng I và bánh xe II (hình 3.9). Bán kính của vô lăng và bánh xe là R1 = 10cm và R2 = 50cm. Vô lăng đang quay với vận tốc 720 vòng/phút thì bị ngắt điện, nó quay chậm dần đều, sau đó 30 giây vận tốc chỉ còn 180 vòng/phút. Tính số vòng quay của vô lăng trong khoảng thời gian 30 giây đó.
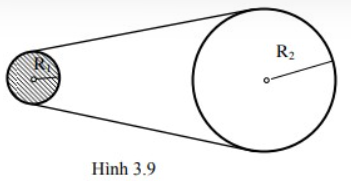
A. 540 vòng
B. 270 vòng
C. 225 vòng
D. 45 vòng
Một dây cuaroa truyền động, vòng qua vô lăng I và bánh xe II (hình 3.9). Bán kính của vô lăng và bánh xe là R1 = 10cm và R2 = 50cm. Vô lăng đang quay với vận tốc 720 vòng/phút thì bị ngắt điện, nó quay chậm dần đều, sau đó 30 giây vận tốc chỉ còn 180 vòng/phút. Tính số vòng quay của bánh xe trong khoảng thời gian 30 giây đó.
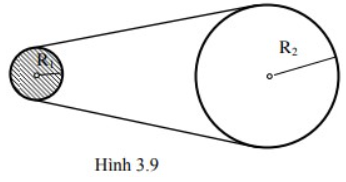
A. 540 vòng
B. 144 vòng
C. 225 vòng
D. 45 vòng
Một dây cuaroa truyền động, vòng qua vô lăng I và bánh xe II (hình 3.9). Bán kính của vô lăng và bánh xe là R1 = 10cm và R2 = 50cm. Vô lăng đang quay với vận tốc 720 vòng/phút thì bị ngắt điện, nó quay chậm dần đều, sau đó 30 giây vận tốc chỉ còn 180 vòng/phút. Sau bao lâu kể từ lúc ngắt điện, hệ thống sẽ dừng?
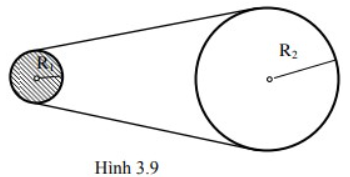
A. 40 giây
B. 50 giây
C. 60 giây
D. 80 giây
Một dây cuaroa truyền động, vòng qua vô lăng I và bánh xe II (hình 3.9). Bán kính của vô lăng và bánh xe là R1 = 10cm và R2 = 50cm. Vô lăng đang quay với vận tốc 720 vòng/phút thì bị ngắt điện, nó quay chậm dần đều, sau đó 30 giây vận tốc chỉ còn 180 vòng/phút. Tính số vòng quay của bánh xe kể từ lúc ngắt điện cho đến khi dừng lại.
A. 480 vòng
B. 240 vòng
C. 45 vòng
D. 48 vòng
Một dây cuaroa truyền động, vòng qua vô lăng I và bánh xe II (hình 3.9). Bán kính của vô lăng và bánh xe là R1 = 10cm và R2 = 50cm. Vô lăng đang quay với vận tốc 720 vòng/phút thì bị ngắt điện, nó quay chậm dần đều, sau đó 30 giây vận tốc chỉ còn 180 vòng/phút. Tính số vòng quay của vô lăng kể từ lúc ngắt điện cho đền khi dừng lại.

A. 480 vòng
B. 240 vòng
C. 225 vòng
D. 48 vòng
Một bánh xe có bán kính R, lăn không trượt trên mặt đường. Quãng đường mà khối tâm của bánh xe đã đi được khi bánh xe quay một vòng quanh trục của nó là:
A. s = 2πR
B. s = πR
C. s = R
D. s = 8R
Một bánh xe có bán kính R, lăn không trượt trên mặt đường. Quãng đường mà một điểm M trên vành bánh xe đã đi được khi bánh xe quay một vòng quanh trục của nó là:
A. s = 2πR
B. s = πR
C. s = R
D. s = 8R
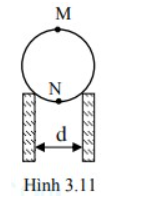
Quả cầu bán kính R = 5cm, lăn đều, không trượt trên hai thanh ray song song cách nhau một khoảng d = 6cm. Sau 2s, tâm quả cầu tịnh tiến được 120cm. Tính vận tốc góc của quả cầu (hình 3.11).
A. 15 rad/s
B. 12 rad/s
C. 10 rad/s
D. 20 rad/s
Quả cầu bán kính R = 5cm, lăn đều, không trượt trên hai thanh ray song song cách nhau một khoảng d = 6cm. Sau 2s, tâm quả cầu tịnh tiến được 120cm. Tính vận tốc tức thời của điểm M trên quả cầu (hình 3.11).

A. 0,6 m/s
B. 1,2 m/s
C. 0,75 m/s
D. 1,35 m/s
Quả cầu bán kính R = 3cm, lăn đều, không trượt trên hai thanh ray song song cách nhau một khoảng d = 4cm. Sau 2s, tâm quả cầu tịnh tiến được 120cm. Tính vận tốc tức thời của điểm N trên quả cầu (hình 3.11).

A. 0,6 m/s
B. 0,15 m/s
C. 0,75 m/s
D. 1,35 m/s
Quả cầu bán kính R = 3cm, lăn đều, không trượt trên hai thanh ray song song cách nhau một khoảng d = 4cm. Sau 2s, tâm quả cầu tịnh tiến được 120cm. Vectơ vận tốc tức thời của điểm N trên quả cầu (hình 3.11) có đặc điểm:

A. Hướng theo hướng chuyển động của quả cầu.
B. Bằng không.
C. Hướng ngược hướng chuyển động của quả cầu.
D. Hướng vào tâm quả cầu.
Cho tam giác đều ABC, cạnh a. Đặt tại các đỉnh A, B, C các chất điểm có khối lượng bằng nhau và bằng m. Đặt thêm một chất điểm có khối lượng 3m tại A. Mômen quán tính đối với trục quay đi qua khối tâm của hệ và vuông góc với mặt phẳng (ABC) là:
A. I = 3ma2
B. I = 3/2 ma2
C. I = 2ma2
D. ma2
Cho tam giác đều ABC, cạnh a. Đặt tại các đỉnh A, B, C các chất điểm có khối lượng bằng nhau và bằng m. Đặt thêm một chất điểm có khối lượng 3m tại A. Mômen quán tính đối với trục quay chứa khối tâm G của hệ và chứa đỉnh A là:
A. I = 3ma2
B. I = 3/2 ma2
C. I = 2ma2
D. I = ½ ma2
Khối cầu đặc đồng chất, tâm O, bán kính R, khối lượng m phân bố đều. Người ta khoét bên trong khối cầu đó một lỗ hổng cũng có dạng hình cầu tâm O’, bán kính r = R/2. Nếu O’ cách O một đoạn d = R/2 thì mômen quán tính của phần còn lại của khối cầu đối với trục quay chứa O và O’ là:
A. \[{\rm{I = }}\frac{{\rm{2}}}{{\rm{5}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
B. \[{\rm{I = }}\frac{{\rm{3}}}{{\rm{2}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
C. \[{\rm{I = }}\frac{{{\rm{31}}}}{{{\rm{70}}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
D. \[{\rm{I = }}\frac{{{\rm{31}}}}{{{\rm{80}}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
Khối cầu đặc đồng chất, tâm O, bán kính R, khối lượng m phân bố đều. Người ta khoét bên trong khối cầu đó một lỗ hổng cũng có dạng hình cầu tâm O’, bán kính r = R/2. Nếu O’ cách O một đoạn d = R/2 thì mômen quán tính của phần còn lại của khối cầu đối với trục quay chứa O và vuông góc với OO’ là:
A. \[{\rm{I = }}\frac{{\rm{2}}}{{\rm{5}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
B. \[{\rm{I = }}\frac{{{\rm{57}}}}{{{\rm{160}}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
C. \[{\rm{I = }}\frac{{{\rm{31}}}}{{{\rm{70}}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
D. \[{\rm{I = }}\frac{{{\rm{31}}}}{{{\rm{80}}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
Một quả cầu đặc đồng chất, tâm O, bán kính R, khối lượng m phân bố đều, được gắn chặt tiếp xúc ngòai với một quả cầu đặc khác, tâm O’, đồng chất với nó nhưng có bán kính gấp đôi. Mômen quán tính của hệ hai quả cầu này đối với trục quay chứa O và O’ là:
A. \[{\rm{I = }}\frac{{{\rm{66}}}}{{\rm{5}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
B. I = mR2
C. \[{\rm{I = }}\frac{{\rm{2}}}{{\rm{5}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
D. \[{\rm{I = }}\frac{{\rm{3}}}{{{\rm{80}}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}\]
