25 câu hỏi
Đỉnh của parabol (P): y = 3x2 – 2x + 1 là:
Hàm số nào say đây có đồ thị là parabol có đỉnh I(-1; 3)?
y = 2x2 – 4x – 3.
y = 2x2 – 2x – 1.
y = 2x2 + 4x + 5.
y = 2x2 + x + 2.
Tìm parabol (P): y = ax2 + 3x – 2, biết rằng parabol cắt trục Ox tại điểm có hoành độ bằng 2.
y = x2 + 3x – 2.
y = -x2 + x – 2.
y = -x2 + 3x – 3.
y = -x2 + 3x – 2.
Tìm parabol (P): y = ax2 + 3x – 2 biết rằng có trục đối xứng x = -3.
y = x2 + 3x – 2.
Tọa độ giao điểm của parabol (P): y = x2 – 4x với đường thẳng (d): y = -x – 2 là:
M(-1; -1) và N(-2; 0).
M(1; -3) và N(2; -4).
M(0; -2) và N(2; -4).
M(-3; 1) và N(3; -5).
Gọi A(a; b) và B(c; d) là tọa độ giao điểm của (P): y = 2x – x2 và (d): y = 3x – 6. Giá trị của b + d bằng:
7.
-7.
15.
-15.
Parabol (P): y = x2 + 4x + 4 có số điểm chung với trục hoành là:
0.
1.
2.
3.
Cho parabol (P): y = x2 – 2x + m – 1. Tìm tất cả các giá trị thực của tham số m để parabol (P) không cắt trục Ox.
m < 2.
m > 2.
Tập xác định của hàm số là:
[3; 4]
R \ (3; 4)
(3; 4)
R \ [3; 4].
Tập xác định của hàm số là:
R.
Miền giá trị của hàm số y = 2x2 – 6 là:
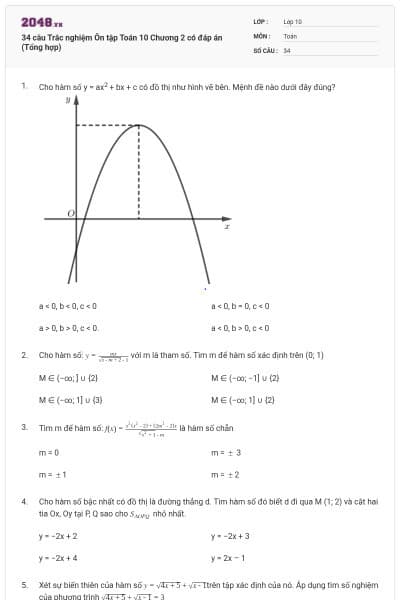
Hình vẽ bên là đồ thị của hàm số nào?
y = -3x + 2.
y = 3x + 2.
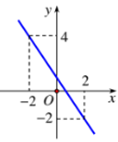
Hình vẽ bên là đồ thị của hàm số nào dưới đây?
y = 10x + 15.
y = 10x + 5.
Tìm tập xác định D của hàm số
D = {1; -4}.
D = R \ {1; -4}.
D = R \ {1; 4}.
D = R.
Tìm tập xác định D của hàm số
D = R.
Tìm tập xác định D của hàm số
D = R.
D = (-4; 4).
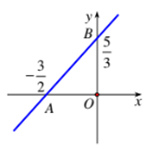
Đồ thị ở hình bên là đồ thị hàm số nào dưới đây?
y = x + 1.
y = -x + 2.
y = 2x + 1.
y = -x + 1.
Bảng biên thiên ở hình bên là bảng biến thiên của hàm số nào sau đây?
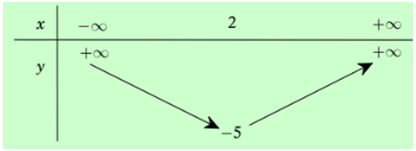
y = -x2 + 4x – 9.
y = x2 – 4x – 1.
y = -x2 + 4x.
y = x2 – 4x – 5.
Bảng biên thiên ở hình bên là bảng biến thiên của hàm số nào sau đây?
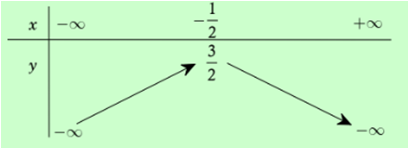
y = 2x2 + 2x – 1.
y = 2x2 + 2x + 2.
y = -2x2 – 2x.
y = -2x2 – 2x + 1.
Đồ thị ở hình bên là đồ thị của hàm số nào dưới đây?
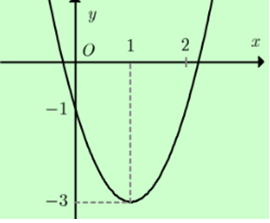
y = x2 – 4x – 1.
y = 2x2 – 4x – 1.
y = -2x2 – 4x – 1.
y = 2x2 – 4x + 1.
Xác định parabol (P): y = ax2 + bx + c biết rằng parabol (P) đi qua ba điểm A(1; 1), B(-1; -3) và O(0; 0).
y = x2 + 2x.
y = -x2 – 2x.
y = -x2 + 2x.
y = x2 – 2x.
Xác định parabol (P): y = ax2 + bx + c biết rằng (P) đi qua M(-5; 6) và cắt trục tung tại điểm có tung độ bằng -2. Mệnh đề nào dưới đây đúng?
a = 6b.
25a – 5b = 8.
b = -6a.
25a + 5b = 8.
Tìm tất cả các giá trị thực của tham số b để đồ thị hàm số y = -3x2 + bx – 3 cắt trục hoành tại hai điểm phân biệt.
b < -6 hoặc b > 6.
–6 < b < 6.
b < -3 hoặc b > 3.
-3 < b < 3.
Cho parabol (P): y = x2 + x+ 2 và đường thẳng (d): y =ax + 1. Tìm tất cả các giá trị thực của tham số a để (P) tiếp xúc với (d).
a = -1; a = 3.
a = 2.
a = 1; a = -3.
Không tồn tại giá trị của a.
Cho parabol (P): y = x2 – 2x + m – 1. Tìm tất cả các giá trị thực của tham số m để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương.
1 < m < 2.
m < 2.
m > 2.
m < 1.