10 câu hỏi
Cho hai biến cố \(A\) và \(B\). Xác suất của biến cố \(A\) với điều kiện biến cố \(B\) đã xảy ra được gọi là xác suất của \(A\) với điều kiện \(B\), ký hiệu là \(P\left( {\left. A \right|B} \right)\). Phát biểu nào sau đây đúng?
Nếu \(P\left( A \right) > 0\) thì \(P\left( {\left. A \right|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}}\).
Nếu \(P\left( B \right) > 0\) thì \(P\left( {\left. A \right|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
Nếu \(P\left( {A \cap B} \right) > 0\) thì \(P\left( {\left. A \right|B} \right) = \frac{{P\left( A \right)}}{{P\left( {A \cap B} \right)}}\).
Nếu \(P\left( {A \cap B} \right) > 0\) thì \(P\left( {\left. A \right|B} \right) = \frac{{P\left( B \right)}}{{P\left( {A \cap B} \right)}}\).
Cho \(A\) và \(B\) là hai biến cố độc lập thoả mãn \({\rm{P}}(A) = 0,5\) và \({\rm{P}}(B) = 0,3\). Khi đó, \({\rm{P}}(A \cap B)\) bằng:
0,8.
0,2.
0,6.
0,15.
Cho hai biến cố \[A\] và \[B\] là hai biến cố xung khắc, với \[P\left( A \right) = 0,3\] và \[P\left( B \right) = 0,5\]. Tính \[P\left( {A|B} \right)\].
\[0,15\].
\[0,3\].
\[0,5\].
\[0\].
Một bình đựng 3 bi xanh và 2 bi trắng. Lấy ngẫu nhiên lần 1 một viên bi (không bỏ vào lại), rồi lần 2 một viên bi. Tính xác suất để lần 1 lấy một viên bi xanh, lần 2 lấy một viên bi trắng.
\[\frac{3}{8}\].
\[\frac{3}{{10}}\].
\[\frac{2}{7}\].
\[\frac{1}{3}\].
Trong hộp có 20 nắp khoen bia Tiger, trong đó có 2 nắp ghi “Chúc mừng bạn đã trúng thưởng xe FORD”. Bạn được chọn lên rút thăm lần lượt hai nắp khoen, tính xác suất để cả hai nắp đều trúng thưởng.
\[\frac{4}{7}\].
\[\frac{1}{{280}}\].
\[\frac{1}{{190}}\].
\[\frac{1}{{75}}\].
Một hộp kín đựng \[30\] tấm thẻ giống hệt nhau đánh số từ \(1\) đến \(30\). Một người rút ngẫu nhiên ra một tấm thẻ từ trong hộp. Người đó được thông báo rằng thẻ rút ra mang số chẵn. Tính xác suất để người đó rút được thẻ có số chia hết cho \(10\).
\(\frac{2}{5}\).
\(\frac{1}{5}\).
\(\frac{3}{{10}}\).
\(\frac{3}{5}\).
Một hộp có \(7\) viên bi cùng kích thước và khối lượng, trong đó có \(4\) viên bi màu đỏ và \(3\) viên bi màu xanh. Lấy ngẫu nhiên lần lượt \(2\) viên bi và không hoàn lại. Xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ bằng
\(\frac{1}{3}\).
\(\frac{3}{4}\).
\(1\).
\(\frac{1}{2}\).
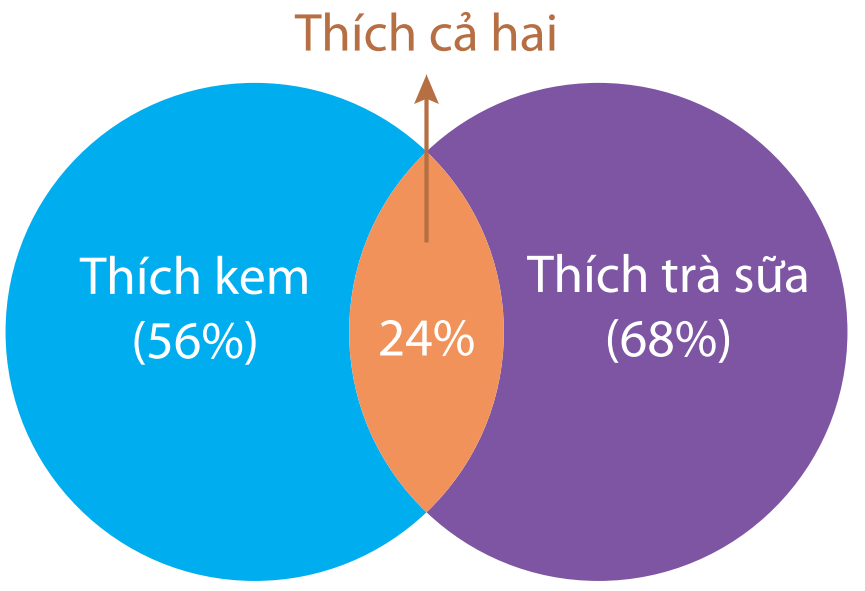
Trong cuộc khảo sát trên một nhóm học sinh gồm các bạn thích trà sữa hoặc kem, người ta có được kết quả sau: Có 56% số học sinh thích kem, 68% số học sinh thích trà sữa, 24% số học sinh thích cả trà sữa và kem (hình bên). Chọn ngẫu nhiên một bạn học sinh trong nhóm được khảo sát này. Xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa bằng
\( \approx 0,35\).
\( \approx 0,29\).
\( \approx 0,43\).
\( \approx 0,32\).
Một công ty vừa ra mắt sản phẩm X và tổ chức ngày trải nghiệm sản phẩm. Họ thống kê được trong \[200\] người đến tham quan ngày trải nghiệm có \[60\] người là nam giới và \[140\] người là nữ giới. Trong số những người được thống kê này, có \[120\] người mua sản phẩm X, gồm \[40\] khách hàng nam và 80 khách hàng nữ, còn lại là không mua sản phẩm X. Chọn ngẫu nhiên một người trong số \[200\] người được thống kê. Xác suất để người này mua sản phẩm X, biết rằng người được chọn là nữ giới bằng bao nhiêu ? (làm tròn kết quả đến hàng phần trăm).
\( \approx 0,45\).
\( \approx 0,57\).
\( \approx 0,34\).
\( \approx 0,72\).
Theo kết quả từ trạm nghiên cứu khí hậu tại địa phương T, xác suất để một ngày có gió là \[0,6\]; nếu ngày có gió thì xác suất có mưa là \[0,4\]; nếu ngày không có gió thì xác suất có mưa là \[0,2\]. Xác suất để trời vừa có gió và vừa có mưa và xác suất để trời có gió nhưng không có mưa lần lượt bằng
\(0,16\) và \(0,24\).
\(0,32\) và \(0,24\).
\(0,24\) và \(0,36\).
\(0,36\) và \(0,48\).
