20 CÂU HỎI
Trường hợp nào sau đây là công thức rút gọn của mạng:
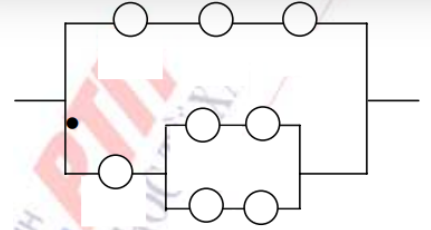
A. \(x \wedge \left( {y \vee z} \right)\)
B. \(x \vee \left( {y \wedge z} \right)\)
C. \(z \wedge \left( {y \vee x} \right)\)
D. \(y \vee \left( {x \wedge z} \right)\)
Trường hợp nào sau đây tập R3 với các phép toán được định nghĩa là không gian véc tơ:
A. \(\left\{ {\begin{array}{*{20}{c}}{(x,y,z) + (x\prime ,y\prime ,x\prime ) = (x + x\prime ,y + y\prime ,z + z\prime }\\{\alpha (x,y,z) = (\alpha x,y,z);\alpha \in R}\end{array}} \right.\)
B. \(\left\{ {\begin{array}{*{20}{c}}{(x,y,z) + (x\prime ,y\prime ,x\prime ) = (x + x\prime ,y + y\prime ,z + z\prime )}\\{\alpha (x,y,z) = (2\alpha x,2\alpha y,2\alpha z);\alpha \in R}\end{array}} \right.\)
C. \(\left\{ {\begin{array}{*{20}{c}}{(x,y,z) + (x\prime ,y\prime ,x\prime ) = (x + x\prime + 1,y + y\prime + 1,z + z\prime + 1)}\\{\alpha (x,y,z) = (0,0,0);\alpha \in R}\end{array}} \right.\)
D. \(\left\{ {\begin{array}{*{20}{c}}{(x,y,z) + (x\prime ,y\prime ,x\prime ) = (x + x\prime ,y + y\prime ,z + z\prime )}\\{\alpha (x,y,z) = (\alpha x,\alpha y,\alpha z);\alpha \in R}\end{array}} \right.\)
Với các phép cộng hai hàm số và phép nhân hàm số với số thực, tập các hàm số nào sau đây là không gian véc tơ:
A. Tập các hàm số không âm trên [a, b]
B. Tập các hàm số bị chặn trên [a, b]
C. Tập các hàm số khả vi trên [a, b] (có đạo hàm tại mọi điểm)
D. Tập các hàm số trên [a, b] sao cho f(b) =1
Tập hợp các véc tơ có dạng nào sau đây không là không gian con của R3 :
A. Các véc tơ có dạng (x, 0, z)
B. Các véc tơ có dạng (x, y, 1)
C. Các véc tơ có dạng (x, y, z) thoả mãn x + y + z = 0
D. Các véc tơ có dạng (x, y, z), 2x – y + z = 0, x + y - 4z = 0
Tập hợp các véc tơ có dạng nào sau đây không là không gian con của R3 :
A. Các véc tơ (x, y, z) thoả mãn\[{\rm{x}} \le {\rm{y}} \le {\rm{z}}\]
B. Các véc tơ (x, y, z) thoả mãn x + y + z = 0
C. Các véc tơ (x, y, z) thoả mãn xy = 0
D. Các véc tơ (x, y, z) thoả mãn 3x + 2y - 4z = 0
Tìm véc tơ u sau của không gian R4 thỏa mãn phương trình: \[{\rm{3(}}{{\rm{v}}_{\rm{1}}} - {\rm{u) + 2(}}{{\rm{v}}_{\rm{2}}}{\rm{ + u) = 5(}}{{\rm{v}}_{\rm{3}}}{\rm{ + u)}}\]trong đó \[{\rm{v}}1 = \left( {2,5,1,3} \right);{\rm{v}}2 = \left( {10,1,5,10} \right);{\rm{v}}3 = (4,1, - 1,1)\]
A. \[{\rm{u}} = (6,12,18,24)\]
B. \[{\rm{u}} = (7, - 2,3,0)\]
C. \[{\rm{u}} = (1,2,3,4)\]
D. \[{\rm{u}} = ( - 2,3,7,0)\]
Hãy xác định \(\lambda \) sao cho x là tổ hợp tuyến tính của u,v,w: \[{\rm{x}} = (7, - 2,{\rm{\lambda }});{\rm{u}} = (2,3,5),{\rm{v}} = (3,7,8),{\rm{w}}( - 1, - 6,1)\]
A. \[{\rm{\lambda }} = 10\]
B. \[{\rm{\lambda }} = - 11\]
C. \[{\rm{\lambda }} = 12\]
D. \[{\rm{\lambda }} = 11\]
Hệ véc tơ nào sau đây của R3 thuộc độc lập tuyến tính:
A. \[{\rm{u}} = (1, - 2,1),{\rm{v}} = (2,1, - 1),{\rm{w}} = (7, - 1,4)\]
B. \[{\rm{u}} = (1, - 3,7),{\rm{v}} = (2,0,8),{\rm{w}} = (8, - 1,8),{\rm{x}}(3, - 9,7)\]
C. \[{\rm{u}} = (1,2, - 3),{\rm{v}} = (1, - 3,2),{\rm{w}} = (2, - 1,5)\]
D. \[{\rm{u}} = (2, - 3,13),{\rm{v}} = (0,0,0),{\rm{w}} = (1, - 10,11)\]
Hệ véc tơ nào dưới đây là độc lập tuyến tính?
A. \[{\rm{u}} = (4, - 2,6),{\rm{v}} = (6, - 3,9)\]trong R3
B. \[{\rm{u}} = (2, - 3,1),{\rm{v}} = (3, - 1,5),{\rm{w}} = (1, - 4,3)\]trong R3
C. \[{\rm{u}} = (5,4,3),{\rm{v}} = (3,3,2),{\rm{w}} = (8,1,3)\]trong R3
D. \[(4, - 5,2,6),{\rm{v}} = (2, - 2,1,3),{\rm{w}} = (6, - 3,3,9),{\rm{s}} = (4 - 1,5,6)\]trong R4
Tìm λ để hệ véc tơ sau phụ thuộc tuyến tính: \[{\rm{u}} = ({\rm{\lambda }},\frac{{ - 1}}{2},\frac{{ - 1}}{2}),{\rm{v}} = (\frac{{ - 1}}{2},{\rm{\lambda }},\frac{{ - 1}}{2}),{\rm{w}} = (\frac{{ - 1}}{2},\frac{{ - 1}}{2},{\rm{\lambda }})\]
A. \[{\rm{\lambda }} = 1\]
B. \[{\rm{\lambda }} = 1,{\rm{\lambda }} = \frac{1}{2}\]
C. \[{\rm{\lambda }} = 2,{\rm{\lambda }} = \frac{1}{2}\]
D. \[{\rm{\lambda }} = - 3\]
Xác định hệ véc tơ nào sau đây là một cơ sở của không gian R3:
A. \[{\rm{u}} = (1, - 2,1),{\rm{v}} = (2,1, - 1)\]
B. \[{\rm{u}} = (2, - 3,13),{\rm{v}} = (2,0,8),{\rm{w}} = (8, - 1,8),{\rm{x}} = (3, - 9,7)\]
C. \[{\rm{u}} = (1,1,1),{\rm{v}} = (1,2,3),{\rm{w}} = (2, - 1,1)\]
D. \[{\rm{u}} = (1,1,2),{\rm{v}} = (1,2,5),{\rm{w}} = (5,3,4)\]
Xác định toạ độ của véc tơ\[{\rm{v}} = (4, - 3,2)\]viết trong cơ sở \[\Re = \left\{ {(1,1,1),(1,1,0),(1,0,0)} \right\}\]của không gian R3:
A. \[{\left[ {\rm{v}} \right]_{\rm{B}}} = (2, - 3,8)\]
B. \[{\left[ {\rm{v}} \right]_{\rm{B}}} = (2, - 5,7)\]
C. \[{\left[ {\rm{v}} \right]_{\rm{B}}} = ( - 2, - 3,8)\]
D. \[{\left[ {\rm{v}} \right]_{\rm{B}}} = (2, - 3, - 8)\]
Tìm chiều của các không gian con của R4:
A. Các véc tơ có dạng (x, y, 0, t)
B. Các véc tơ có dạng (x, y, z, t) với z = x - y và t = x + y
C. Các véc tơ có dạng (x, y, z, t) với x = y = z = t
D. Các véc tơ có dạng (x, y, z, t) với x = 2y + z − 3t
Tìm hạng r của hệ véc tơ sau của không gian R4: \[{{\rm{v}}_1} = (1,2,3,4);{{\rm{v}}_2} = (2,3,4,5);{{\rm{v}}_3} = (3,4,5,6);{{\rm{v}}_4} = (4,5,6,7)\]
A. r = 4
B. r = 2
C. r = 3
D. r = 1
Phép toán nào sau đây không thực hiện được:
A. \[\left( {\begin{array}{*{20}{c}}1&2\\5&0\end{array}\,\,\,\,\,\begin{array}{*{20}{c}}{ - 3}&6\\7&9\end{array}} \right) + \left( {\begin{array}{*{20}{c}}{ - 5}&1\\{ - 2}&8\end{array}\,\,\,\,\,\begin{array}{*{20}{c}}{ - 3}&0\\{ - 4}&2\end{array}} \right)\]
B. \[\left( {\begin{array}{*{20}{c}}1&{2\,\,\,\,\,5}\\3&{4\,\,\,\,\,\,7}\end{array}} \right) + \left( {\begin{array}{*{20}{c}}4&3\\2&9\end{array}} \right)\]
C. \[ - 3\left( {\begin{array}{*{20}{c}}1&2\\5&0\end{array}\,\,\,\,\,\begin{array}{*{20}{c}}{ - 3}&6\\7&9\end{array}} \right)\]
D. \[0\left( {\begin{array}{*{20}{c}}{ - 5}&1\\{ - 2}&8\end{array}\,\,\,\,\,\begin{array}{*{20}{c}}{ - 3}&0\\{ - 4}&2\end{array}} \right)\]
Phép biến đổi nào sau đây không phải là phép biến đổi tương đương của hệ phương trình:
A. Thay đổi vị trí của hai phương trình của hệ
B. Nhân một số bất kỳ vào cả 2 vế của một phương trình của hệ
C. Cộng một phương trình vào một phương trình khác của hệ (vế với vế)
D. Trừ một phương trình vào một phương trình khác của hệ
Tìm các giá trị của tham số m để hệ phương trình sau có duy nhất nghiệm:
\[\left\{ {\begin{array}{*{20}{c}}{(m - 1){x_1} + {x_2} + {x_3} + {x_4} = 1}\\{{x_1} + (m - 1){x_2} + {x_3} + {x_4} = 2}\\{{x_1} + {x_2} + (m - 1){x_3} + {x_4} = 3}\\{{x_1} + {x_2} + {x_3} + (m - 1){x_4} = 4}\end{array}} \right.\]
A. \[{\rm{m}} \ne \pm 2\]
B. \[{\rm{m}} \ne 1;{\rm{m}} \ne 3\]
C. \[{\rm{m}} \ne - 3;{\rm{m}} \ne 1\]
D. \[{\rm{m}} \ne - 2;{\rm{m}} \ne 3\]
Cho hệ phương trình tuyến tính:\(\left\{ {\begin{array}{*{20}{c}}{9{x_1} + {x_2} + 4{x_3} = 1}\\{2{x_1} + 2{x_2} + 3{x_3} = 5}\\{7{x_1} + {x_2} + 6{x_3} = 7}\end{array}} \right.\)
Tính các định thức\[{\rm{D, }}{{\rm{D}}_{\rm{1}}}{\rm{, }}{{\rm{D}}_{\rm{2}}}{\rm{, }}{{\rm{D}}_{\rm{3}}}\]
A. \[{\rm{D = 22, }}{{\rm{D}}_{\rm{1}}}{\rm{ = 16, }}{{\rm{D}}_{\rm{2}}}{\rm{ = }} - {\rm{6, }}{{\rm{D}}_{\rm{3}}}{\rm{ = 19}}\]
B. \[{\rm{D}} = 13,{{\rm{D}}_1} = - 16,{{\rm{D}}_2} = 14,{{\rm{D}}_3} = 19\]
C. \[{\rm{D}} = 42,{{\rm{D}}_1} = - 36,{{\rm{D}}_2} = 6,{{\rm{D}}_3} = 90\]
D. \[{\rm{D}} = 42,{{\rm{D}}_1} = - 36,{{\rm{D}}_2} = 6,{{\rm{D}}_3} = 90\]
Giải hệ phương trình tuyến tính \(\left\{ {\begin{array}{*{20}{c}}{4{x_1} + 3{x_2} + {x_3} + 5{x_4} = 7}\\{{x_1} - 2{x_2} - 2{x_3} - 3{x_4} = 3}\\{3{x_1} - {x_2} + 2{x_3} = - 1}\\{2{x_1} + 3{x_2} + 2{x_3} - 8{x_4} = - 7}\end{array}} \right.\)
A. \[{{\rm{x}}_1} = 2,{{\rm{x}}_2} = 1,{{\rm{x}}_3} = 2,{{\rm{x}}_4} = 1\]
B. \[{{\rm{x}}_1} = - 3,{{\rm{x}}_2} = 1,{{\rm{x}}_3} = 2,{{\rm{x}}_4} = - 1\]
C. \[{{\rm{x}}_1} = - 3,{{\rm{x}}_2} = - 1,{{\rm{x}}_3} = 2,{{\rm{x}}_4} = - 1\]
D. \[{{\rm{x}}_1} = 4,{{\rm{x}}_2} = - 5,{{\rm{x}}_3} = 7,{{\rm{x}}_4} = 3\]
Hệ véc tơ nào sau đây sinh ra R3
A. \[{\rm{u}} = (2,1, - 3),{\rm{v}} = (3,2, - 5),{\rm{w}}(1, - 1,1)\]
B. \[{\rm{u}} = (2, - 1,3),{\rm{v}} = (4,1,2),{\rm{w}} = (8, - 1,8)\]
C. \[{\rm{u}} = (3,1,4),{\rm{v}} = (2, - 3,5),{\rm{w}} = (5, - 2,9),{\rm{s}} = (1,4, - 1)\]
D. \[{\rm{u}} = (3,1,13),{\rm{v}} = (2,7,4),{\rm{w}} = (1, - 10,11)\]
