12 CÂU HỎI
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số f(x) có bảng biến thiên như sau
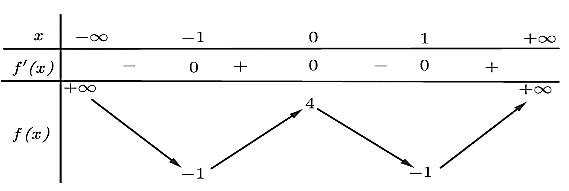
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(−∞; −1).
(0; 1).
(−1; 1).
(−1; 0).
Cho hàm số y = f(x) có bảng biến thiên như sau
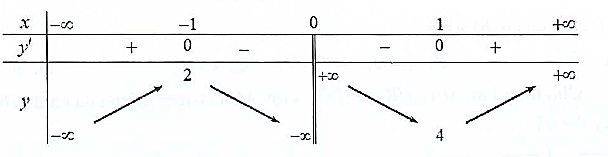
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
(−1; 1).
(4; +∞).
(−∞; 2).
(0; 1).
Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau
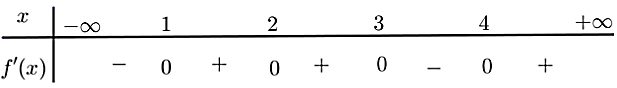
Hàm số nghịch biến trên khoảng nào dưới đây?
(−∞; 1).
(2; 4).
(1; 3).
(3; +∞).
Cho hàm số f(x) xác định trên ℝ và có bảng xét dấu đạo hàm f'(x) như sau:
Khẳng định nào sau đây đúng?
f(−1) > f(3).
f(6) > f(8).
f(−3) > f(−1).
f(5) < f(6).
Cho hàm số y = f(x) có đồ thị như hình.
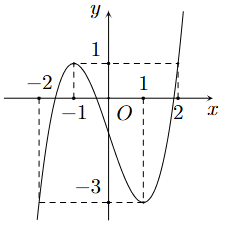
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
(0; 2).
(1; +∞).
(−∞; 1).
(−2; 1).
Cho hàm số 
. Mệnh đề nào dưới đây là đúng?
Hàm số nghịch biến trên ℝ.
Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞).
Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).
Hàm số đồng biến trên ℝ\{2}.
Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ.
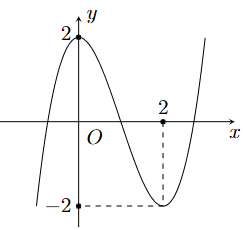
Hàm số y = f(x) đạt cực tiểu tại điểm nào dưới đây?
x = 2.
x = 0.
x = −2.
x = 4.
Cho hàm số y = f(x) có bảng biến thiên như sau
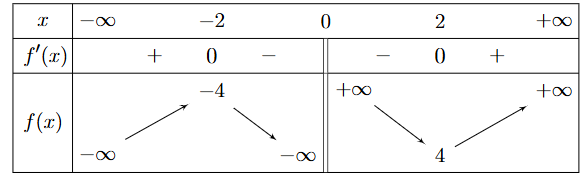
Khẳng định nào sau đây sai?
Hàm số có hai điểm cực trị.
Tọa độ điểm cực đại của đồ thị hàm số là (−2; −4).
Hàm số nghịch biến trên khoảng (−2; 2).
Hàm số đồng biến trên khoảng (3; +∞).
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ, a ≠ 0) có đồ thị là đường cong như hình
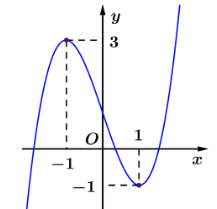
Giá trị cực đại của hàm số đã cho bằng
1.
0.
−1.
3.
Cho hàm số y = f(x) có đạo hàm f'(x) = x2(x + 2)(x2 – 1), ∀x Î ℝ. Số điểm cực trị của hàm số đã cho là
1.
0.
2.
3.
Điểm cực tiểu của hàm số 
là
x = −3.
x = −6.
x = 2.
x = 1.
Cho hàm số y = x3 – 3x + 2. Hàm số đã cho có bao nhiêu cực trị?
2.
0.
1.
3.