12 câu hỏi
Tìm tập xác định \(D\) của hàm số \(y = \frac{{2021}}{{\sin x}}.\)
\(D = \mathbb{R}.\)
\[D = \mathbb{R}\backslash \left\{ 0 \right\}.\]
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\]
Trong các hàm số sau đây, hàm số nào không tuần hoàn?
\(y = \cos x.\)
\(y = \cos 2x.\)
\(y = {x^2}\cos x\).
\(y = \frac{1}{{\sin 2x}}.\)
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
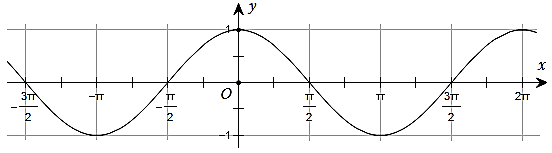
Hỏi hàm số đó là hàm số nào?
\[y = 1 + \sin 2x.\]
\[y = \cos x.\]
\[y = - \sin x.\]
\[y = - \cos x.\]
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y = 3\sin x - 2.\)
\(M = 1,{\rm{ }}m = - 5.\)
\(M = 3,{\rm{ }}m = 1.\)
\(M = 2,{\rm{ }}m = - 2.\)
\(M = 0,{\rm{ }}m = - 2.\)
Trong các hàm số sau, hàm số nào là hàm số chẵn?
\(y = \sin 2x.\)
\(y = x\cos x.\)
\(y = \cos x.\cot x.\)
\(y = \frac{{\tan x}}{{\sin x}}.\)
Tìm tập giá trị \(T\) của hàm số \(y = 3\cos 2x + 5.\)
\(T = \left[ { - 1;1} \right].\)
\(T = \left[ { - 1;11} \right].\)
\(T = \left[ {2;8} \right].\)
\(T = \left[ {5;8} \right].\)
Hàm số \(y = 5 + 4\sin 2x\cos 2x\) có tất cả bao nhiêu giá trị nguyên?
\(3.\)
\(4.\)
\(5.\)
\(6.\)
Gọi \(M,{\rm{ }}m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \sin x + \cos x\). Tính \(P = M - m.\)
\(P = 4.\)
\(P = 2\sqrt 2 .\)
\(P = \sqrt 2 .\)
\(P = 2.\)
Tìm chu kì \(T\) của hàm số \(y = \cos 2x + \sin \frac{x}{2}.\)
\(T = 4\pi .\)
\(T = \pi .\)
\(T = 2\pi .\)
\(T = \frac{\pi }{2}.\)
Tìm chu kì \(T\) của hàm số \[y = \cos 3x + \cos 5x.\]
\(T = \pi .\)
\(T = 3\pi .\)
\(T = 2\pi .\)
\(T = 5\pi .\)
Hàm số nào sau đây có chu kì khác \(\pi \)?
\(y = \sin \left( {\frac{\pi }{3} - 2x} \right).\)
\(y = \cos 2\left( {x + \frac{\pi }{4}} \right).\)
\(y = \tan \left( { - 2x + 1} \right).\)
\(y = \cos x\sin x.\)
Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
\(y = \frac{1}{{{{\sin }^3}x}}.\)
\(y = \sin \left( {x + \frac{\pi }{4}} \right).\)
\(y = \sqrt 2 \cos \left( {x - \frac{\pi }{4}} \right).\)
\(y = \sqrt {\sin 2x} .\)
