22 câu Trắc nghiệm Toán 11 Cánh diều Bài 3. Hàm số mũ. Hàm số lôgarit (Đúng-sai, trả lời ngắn) có đáp án
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong các hàm số sau, hàm số nào không phải là hàm số mũ?
\(y = {\left( {\sqrt 2 } \right)^x}\).
\(y = {8^{\frac{x}{2}}}\).
\(y = {2^{ - x}}\).
\(y = {x^{ - 2}}\).
Trong các hàm số sau, hàm số nào không phải là hàm số lôgarit?
\(y = \log x\).
\(y = {\log _{0,9}}x\).
\(y = {\log _{\sqrt {0,9} }}x\).
y = (x + 3)ln2.
Tập xác định của hàm số y = 7x.
(0; +∞).
(−∞; 0).
ℝ\{0}.
ℝ.
Tập xác định của hàm số y = log2x là
[0; +∞).
(−∞; +∞).
(0; +∞).
[2; +∞).
Tập xác định của hàm số \(y = {\log _3}\sqrt {{x^2} - 9x + 20} \).
(4; 5).
(−∞; 4] È [5; +∞).
(−∞; 4) È (5; +∞).
[4; 5].
Hàm số nào sau đây luôn đồng biến trên tập xác định.
y = 0,3x.
\(y = {\log _{\frac{1}{3}}}x\).
\(y = {\log _{\frac{3}{2}}}x\).
\(y = {\left( {\frac{2}{3}} \right)^x}\).
Hàm số nào trong các hàm số sau đây nghịch biến trên ℝ.
y = log5x.
y = 5x.
y = 0,5x.
y = log0,5x.
Đồ thị hình bên dưới là đồ thị của hàm số nào?
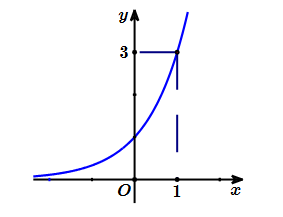
y = 2x.
\(y = {\left( {\frac{1}{2}} \right)^x}\).
\(y = {\left( {\frac{1}{3}} \right)^x}\).
y = 3x.
Đồ thị sau là đồ thị của hàm số nào?
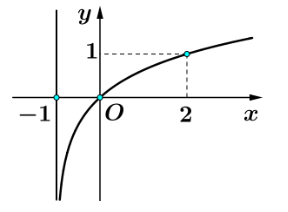
y = log2x + 1.
y = log2(x + 1).
y = log3x.
y = log3(x + 1).
Cho đồ thị hàm số y = ax; y = bx; y = logcx như hình vẽ. Tìm mối liên hệ của a, b, c.
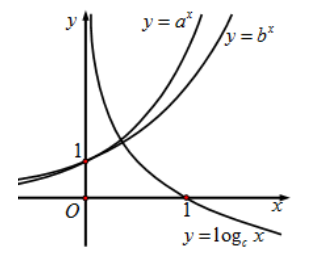
c < b < a.
b < a < c.
a < b < c.
c < a < b.
Điểm M thuộc đồ thị hàm số y = log2(x – 5) có hoành độ bằng 7 thì nhận tung độ bằng
3.
1.
2.
4.
Cho các hàm số y = log4x; y = log2(x – 1); y = log2(x – 5); \(y = {\log _{\sqrt 3 }}x\). Có bao nhiêu đồ thị hàm số đi qua điểm M(3; 1).
3.
1.
2.
4.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số y = log2x. Khi đó
a) Hàm số có tập xác định là ℝ.
b) Tập giá trị của hàm số là khoảng (0; +∞).
c) Đồ thị hàm số cắt trục Oy.
d) Hàm số đồng biến trong khoảng (0; +∞).
Cho hàm số y = f(x) \( = {\log _{\frac{1}{2}}}x\).
a) Ta có f(8) > 0.
b) Với a > 0; b > 0 thì f(ab) = f(a) + f(b).
c) Hàm số đồng biến trên khoảng (0; +∞).
d) Đồ thị hàm số luôn nằm phía trên trục hoành.
Cho hàm số y = f(x) có đồ thị như hình bên dưới
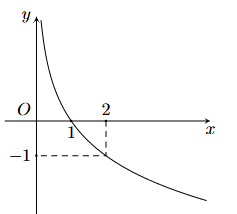
a) Hàm số có dạng y = ax (a > 0; a ≠ 1).
b) Hàm số y = f(x) có tập xác định D = ℝ và tập giá trị T = (0; +∞).
c) Hàm số đồng biến trên khoảng (0; +∞).
d) \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = + \infty \).
Cho hàm số y = 5x.
a) Hàm số đã cho đồng biến trên khoảng (0; 1).
b) Tập xác định của hàm số là khoảng (0; +∞).
c) Đồ thị hàm số y = 5x cắt đường thẳng y = −x + 2 tại điểm có hoành độ dương.
d) Tập giá trị của hàm số là ℝ.
Cho các hàm số \(y = {\log _{\frac{1}{2}}}x\) và y = 2x. Khi đó
a) Có hai hàm số mũ.
b) Đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) đi qua điểm M(2; −1).
c) Đồ thị hàm số y = 2x đi qua điểm N(1; −1).
d) Hai đồ thị hàm số y = 2x và \(y = {\log _{\frac{1}{2}}}x\) cắt nhau tại 1 điểm.
PHẦN II. TRẢ LỜI NGẮN
Tập xác định của hàm số y = log2(x2 – 1) là D = (−∞; b) È (a; +∞). Tính a – b.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = log(x2 – 2mx + 4) xác định với mọi x Î ℝ.
Để dự báo dân số của một quốc gia, người ta sử dụng công thức S = Aenr; trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2020 (lấy làm mốc tính), dân số một nước là 100 triệu người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,8%, dự báo dân số nước đó năm 2035 là bao nhiêu triệu người (kết quả làm tròn đến chữ số hàng đơn vị)?
Trong một phòng thí nghiệm, người ta nuôi một loại vi khuẩn. Ban đầu có 300 vi khuẩn và sau 1 giờ thì số vi khuẩn là 705 con. Giả sử số vi khuẩn tại thời điểm (giờ) được tính theo hàm mũ là f(x) = Cekx với C và k là các hằng số thực dương. Xác định số vi khuẩn sau 5 giờ tính theo đơn vị nghìn con (kết quả làm tròn đến hàng phần mười).
Ngân hàng thường tính lãi suất cho khách hàng theo thể thức lãi kép theo định kì, tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp. Nếu một người gửi số tiền P với lãi suất r mỗi kì thì sau N kì, số tiền người đó thu được (cả vốn lẫn lãi) được tính theo công thức lãi kép sau: A = P(1 + r)N.
Bác Nam gửi tiết kiệm số tiền 100 triệu đồng kì hạn một năm với lãi suất 8% một năm. Giả sử lãi suất không thay đổi. Hỏi số tiền lãi bác Nam thu được sau 10 năm là bao nhiêu triệu đồng? (làm tròn kết quả đến chữ số hàng đơn vị).

