12 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong các hàm số sau, hàm số nào không phải là hàm số mũ?
\(y = {\left( {\sqrt 2 } \right)^x}\).
\(y = {8^{\frac{x}{2}}}\).
\(y = {2^{ - x}}\).
\(y = {x^{ - 2}}\).
Trong các hàm số sau, hàm số nào không phải là hàm số lôgarit?
\(y = \log x\).
\(y = {\log _{0,9}}x\).
\(y = {\log _{\sqrt {0,9} }}x\).
y = (x + 3)ln2.
Tập xác định của hàm số y = 7x.
(0; +∞).
(−∞; 0).
ℝ\{0}.
ℝ.
Tập xác định của hàm số y = log2x là
[0; +∞).
(−∞; +∞).
(0; +∞).
[2; +∞).
Tập xác định của hàm số \(y = {\log _3}\sqrt {{x^2} - 9x + 20} \).
(4; 5).
(−∞; 4] È [5; +∞).
(−∞; 4) È (5; +∞).
[4; 5].
Hàm số nào sau đây luôn đồng biến trên tập xác định.
y = 0,3x.
\(y = {\log _{\frac{1}{3}}}x\).
\(y = {\log _{\frac{3}{2}}}x\).
\(y = {\left( {\frac{2}{3}} \right)^x}\).
Hàm số nào trong các hàm số sau đây nghịch biến trên ℝ.
y = log5x.
y = 5x.
y = 0,5x.
y = log0,5x.
Đồ thị hình bên dưới là đồ thị của hàm số nào?
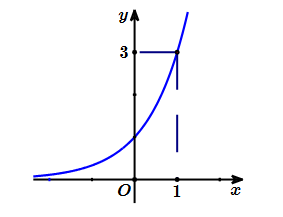
y = 2x.
\(y = {\left( {\frac{1}{2}} \right)^x}\).
\(y = {\left( {\frac{1}{3}} \right)^x}\).
y = 3x.
Đồ thị sau là đồ thị của hàm số nào?
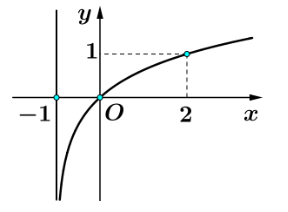
y = log2x + 1.
y = log2(x + 1).
y = log3x.
y = log3(x + 1).
Cho đồ thị hàm số y = ax; y = bx; y = logcx như hình vẽ. Tìm mối liên hệ của a, b, c.
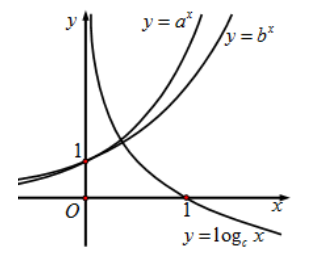
c < b < a.
b < a < c.
a < b < c.
c < a < b.
Điểm M thuộc đồ thị hàm số y = log2(x – 5) có hoành độ bằng 7 thì nhận tung độ bằng
3.
1.
2.
4.
Cho các hàm số y = log4x; y = log2(x – 1); y = log2(x – 5); \(y = {\log _{\sqrt 3 }}x\). Có bao nhiêu đồ thị hàm số đi qua điểm M(3; 1).
3.
1.
2.
4.
