12 CÂU HỎI
Đồ thị hàm số \({\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R})\) ở hình bên có đường tiệm cận xiên là một trong bốn đường thẳng dưới đây, đường thẳng đó là đường nào?
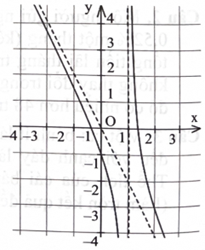
A. \({\rm{y}} = 2{\rm{x}}.\)
B. \({\rm{x}} = 1.\)
C. \({\rm{y}} = - 2{\rm{x}}.\)
D. \(y = - 3x.\)
Nếu một khối chóp có diện tích mặt đáy bằng S và có chiều cao bằng h thì có thể tích bằng
A. \(\frac{{{\rm{Sh}}}}{3}.\)
B. Sh.
C. 3 Sh.
D. \(\frac{{\pi {\rm{Sh}}}}{3}.\)
Tất cả các nghiệm của phương trình \(\cos x = \frac{{ - \sqrt 2 }}{2}\) là
A. \(x = \frac{{3\pi }}{4} + {\rm{k}}\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
B. \({\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}\frac{\pi }{2},{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}\frac{\pi }{2},\forall {\rm{k}} \in \mathbb{Z}.\)
C. \({\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}2\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}2\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
D. \({\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}3\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}3\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
Nếu cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công bội \(q = 3\) thì số hạng \({u_n}\) bằng
A. \({3^{\rm{n}}}.\)
B. \({3^{{\rm{n}} - 1}}.\)
C. \({3^{{\rm{n}} + 1}}.\)
D. \(3 + ({\rm{n}} - 1) \cdot 3.\)
Tập nghiệm của bất phương trình \({\log _{0,5}}x > 4\) là
A. \(\left( {{4^{0,5}}; + \infty } \right).\)
B. \(\left( { - \infty ;{4^{0,5}}} \right).\)
C. \((0;2).\)
D. \(\left( {0;{{(0,5)}^4}} \right).\)
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow {\rm{u}} = ( - {\rm{a}};{\rm{b}};{\rm{c}}),{\overrightarrow {\rm{u}} ^\prime } = (1; - 2;3).\) Toạ độ của vectơ \(\overrightarrow {\rm{u}} + \overrightarrow {{u^\prime }} \) là
A. \(( - {\rm{a}} + 1;{\rm{b}} - 2;{\rm{c}} + 3).\)
B. \(({\rm{a}} + 1;{\rm{b}} - 2;{\rm{c}} + 3).\)
C. \(( - {\rm{a}} + 1;{\rm{b}} + 2;{\rm{c}} + 3).\)
D. \((a + 1;b + 2;{\rm{c}} + 3).\)
Trong không gian Oxyz, tọa độ của vectơ \(\overrightarrow {\rm{u}} = 2\overrightarrow {\rm{j}} - 3\overrightarrow {\rm{k}} \) là
A. \((0; - 2; - 3).\)
B. \((0; - 2;3).\)
C. \((0;2; - 3).\)
D. \((0;2;3).\)
Phát biểu nào sau đây là đúng về mối quan hệ của các đường thẳng trong không gian?
A. Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b song song với nhau.
B. Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b vuông góc với nhau.
C. Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b không có điểm chung
D. Nếu hai đường thẳng \({\rm{a}},{\rm{b}}\) cắt nhau và cùng vuông góc với đường thẳng c thì đường thẳng c vuông góc với mặt phẳng chứa a và b.
Nếu hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục và nhận giá trị dương trên tập số thực thì diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\), trục Ox và các đường thẳng \({\rm{x}} = 7;{\rm{x}} = 9\) bằng
A. \(\int_9^7 | f(x)|dx.\)
B. \(\int_7^9 f (x)dx.\)
C. \(\pi \int_7^9 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.\)
D. \(\pi \int_9^7 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.\)
Nếu các biến cố \({\rm{A}},{\rm{B}}\) thoả mãn \({\rm{P}}({\rm{A}} \cap {\rm{B}}) = 0,2;{\rm{P}}({\rm{B}}) = 0,5\) thì
A. \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,3.\)
B. \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,7.\)
C. \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,01.\)
D. \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,4.\)
Phát biểu nào sau đây là đúng?
A. \(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \ln (1 - 2{\rm{x}}) + C.\)
B. \(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \ln |1 - 2{\rm{x}}| + C.\)
C. \(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \frac{1}{2}\ln |1 - 2{\rm{x}}| + C.\)
D. \(\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \frac{{ - 1}}{2}\ln |1 - 2{\rm{x}}| + C.\)
Cho hình chóp \({\rm{S}}.{\rm{ABCD}}\) có tất cả các cạnh bằng nhau. Số đo góc giữa hai đường thẳng SA và CD bằng
A. \({60^o }.\)
B. \({30^o }.\)
C. \({45^o }.\)
D. \({90^o }.\)

