10 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn, yêu cầu chọn phương án đúng nhất)
Điền vào “...” biểu thức thích hợp để được đẳng thức đúng: \(x{y^2} + y - xy = ...\left( {x - 1 - xy} \right).\)
\( - y\)
\(y.\)
\(x.\)
\( - x.\)
Biểu thức \(x\left( {x + 5} \right) - 8x\) được viết dưới dạng:
\(x\left( {3x - 1} \right).\)
\(x\left( {x - 3} \right).\)
\(x\left( {1 - 3x} \right).\)
\(x\left( {3 - x} \right).\)
Phân tích đa thức \({x^3} - x\) thành nhân tử ta được:
\(x\left( {x - 1} \right).\)
\({x^2}\left( {x - 1} \right).\)
\(x\left( {x + 1} \right)\left( {1 - x} \right).\)
\(x\left( {x + 1} \right)\left( {x - 1} \right).\)
Phân tích đa thức \(\frac{{{x^3}}}{{64}} + 8{y^3}\) thành nhân tử, ta được các nhân tử là:
\(\frac{x}{4} + 2y\) và \(\frac{x}{4} - 2y.\)
\(\frac{x}{4} + 2y\) và \(\frac{{{x^2}}}{{16}} - \frac{{xy}}{2} + 4{y^2}.\)
\(\frac{x}{4} + 2y\) và \(\frac{{{x^2}}}{{16}} + \frac{{xy}}{2} + 4{y^2}.\)
\(\frac{x}{4} + 2y\) và \(2y - \frac{x}{4}.\)
Tổng các giá trị của \(x\) thỏa mãn \({x^2} + 6x = 0\) là:
\( - 4.\)
\( - 6.\)
\(6.\)
\(4.\)
Đa thức nào dưới đây khi phân tích thành nhân tử gồm hai phần tử là \(x + y\) và
\({x^3} - {y^3}.\)
\( - {y^2} - {x^2}.\)
\({x^2} - {y^2}.\)
\({x^2} + {y^2}.\)
Giá trị của biểu thức \({x^2}y + 2x - x{y^2} - 2y\) tại \(x = 2\;026,\;y = 2\;026\) bằng:
\(1.\)
\(0.\)
\( - 1.\)
\( - 2\;{026^2}.\)
Phân tích biểu thức \(\left( {a - b} \right)m + \left( {b - a} \right)n - b + a\) thành tích các đa thức ta được:
\(\left( {b - a} \right)\left( {m - n - 1} \right).\)
\(\left( {a - b} \right)\left( {m - n - 1} \right).\)
Giá trị của biểu thức là
33 000
34 000
35 000
36 000
Một mảnh vườn hình vuông có độ dài cạnh bằng \(x{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\) Người ta định trồng hoa xung quanh mảnh vườn, có độ rộng như nhau và bằng \(y{\rm{ }}\left( {\rm{m}} \right)\) (như hình vẽ).
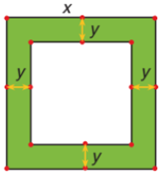
Gọi \(S\) là phần diện tích trồng hoa thì phân tích \(S\) thành nhân tử ta được:
\(4y\left( {x - y} \right).\)
\(2y\left( {x - y} \right).\)
\(y\left( {x - y} \right).\)
\(2y\left( {x - y} \right).\)
