20 câu trắc nghiệm Toán 8 Kết nối tri thức Bài 35. Định lí Pythagore và ứng dụng (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong một tam giác, nếu bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại thì tam giác đó là tam giác gì?
Tam giác nhọn.
Tam giác đều.
Tam giác vuông.
Tam giác tù.
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 8\;{\rm{cm,}}\;AC = 15\;{\rm{cm}}{\rm{.}}\) Tính độ dài \(BC.\)
\(BC = 12\;{\rm{cm}}.\)
\(BC = 21\;{\rm{cm}}.\)
\(BC = 19\;{\rm{cm}}.\)
\(BC = 17\;{\rm{cm}}.\)
Cho tam giác \(ABC\) có \(AB = 21\;{\rm{cm,}}\;AC = 20\;{\rm{cm}},\;BC = 29\;{\rm{cm}}{\rm{.}}\) Tình số đo góc \(A.\)
\(\widehat A = 90^\circ .\)
\(\widehat A = 80^\circ .\)
\(\widehat A = 100^\circ .\)
\(\widehat A = 110^\circ .\)
Cho tam giác \(PQR\) vuông tại \(Q.\) Khi đó:
\(QR = PR - PQ.\)
\(Q{R^2} = P{R^2} - P{Q^2}.\)
\(Q{R^2} = P{R^2} + P{Q^2}.\)
\(Q{R^2} = P{R^2} \cdot P{Q^2}.\)
Cho \(\Delta MNP\) vuông tại \(M\) có \(MN = 4\;{\rm{cm,}}\;NP = \sqrt {32} \;{\rm{cm}}{\rm{.}}\) Tính số đo góc \(N.\)
\(\widehat N = 30^\circ .\)
\(\widehat N = 40^\circ .\)
\(\widehat N = 45^\circ .\)
\(\widehat N = 50^\circ .\)
Cho \(\Delta ABC\) vuông cân tại \(A\) có \(AC = 12\;{\rm{cm}}{\rm{.}}\) Tính độ dài \(BC.\)
\(BC = 144\;{\rm{cm}}.\)
\(BC = \sqrt {288} \;{\rm{cm}}.\)
\(BC = 288\;{\rm{cm}}.\)
\(BC = 24\;{\rm{cm}}.\)
Cho hình vẽ sau:
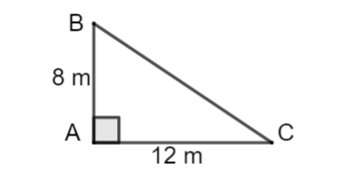
Tính độ dài \(BC.\)
\(BC = 196\;{\rm{m}}.\)
\(BC = 16\;{\rm{m}}.\)
\(BC = 20\;{\rm{m}}.\)
\(BC = \sqrt {208} \;{\rm{m}}.\)
Cho \(\Delta ABC\) vuông tại \(A\) và \(\Delta MNP\) vuông tại \(M\) có \(AB = MN,\;AC < MP.\) Khi đó:
\(BC = NP.\)
\(BC < NP.\)
\(BC > NP.\)
\(BC \ge NP.\)
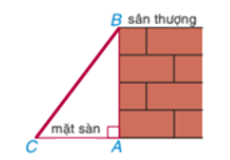
Bác thợ xây muốn xây một cầu thang bắc từ sàn lên sân thượng (như hình vẽ). Biết rằng bức tường từ mặt sàn lên sân thượng cao \(5\;{\rm{m,}}\) chân cầu thang cách bức tường \(3\;{\rm{m}}{\rm{.}}\) Tính chiều dài của cầu thang.
\(8\;{\rm{m}}.\)
\(\sqrt {34} \;{\rm{m}}.\)
\(15\;{\rm{m}}.\)
\(20\;{\rm{m}}.\)
Cho hình vẽ:
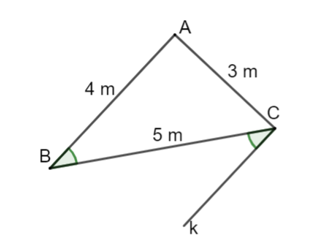
Tính số đo \(\widehat {ACk}.\)
\(\widehat {ACk} = 90^\circ .\)
\(\widehat {ACk} = 80^\circ .\)
\(\widehat {ACk} = 85^\circ .\)
\(\widehat {ACk} = 95^\circ .\)
Cho \(\Delta ABC\) có đường cao \(AH.\) Biết rằng \(HB = 4\;{\rm{m, }}AB = \sqrt {80} \;{\rm{m,}}\;AC = 10\;{\rm{m}}{\rm{.}}\)
\(AH = 8\;{\rm{m}}{\rm{.}}\)
\(CH = 9\;{\rm{m}}{\rm{.}}\)
Chu vi \(\Delta AHC\)bằng \(40\;{\rm{m}}.\)
Chu vi \(\Delta ABC\) lớn hơn chu vi \(\Delta AHC\) khoảng \(15\;{\rm{m}}{\rm{.}}\) (Kết quả làm tròn đến hàng đơn vị).
Cho \(\Delta ABC\) vuông tại \(A\) có chu vi bằng \(48\;{\rm{cm}}\) và \(\frac{{AB}}{{AC}} = \frac{3}{4}.\)
\(\frac{{BC}}{5} = \frac{{AB}}{4}.\)
\(\frac{{AB}}{4} = \frac{{AC}}{3} = \frac{{BC}}{5} = 2.\)
\(BC = 20\;{\rm{cm}}{\rm{.}}\)
Diện tích \(\Delta ABC\)bằng \(96\;{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
Cho hình vẽ:
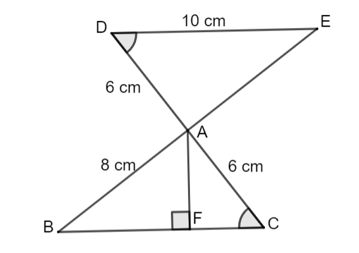
Khi đó:
\(\Delta ADE = \Delta ABC.\)
\(\Delta ABC\) vuông tại \(A.\)
Diện tích \(\Delta ABC\)bằng \(24\;{\rm{c}}{{\rm{m}}^2}.\)
\(AF = 3,6\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC\) cân tại \(A\) có \(AB = 12\;{\rm{cm, }}BC = 6\;{\rm{cm}}{\rm{.}}\) Gọi \(D\) là trung điểm của \(BC.\) Gọi \(E\) là điểm thuộc tia đối của tia \(DA\) sao cho \(DE = \frac{1}{4}AE.\)
\(\Delta ADC\) vuông tại \(D.\)
\(AD = \sqrt {135} \;{\rm{cm}}{\rm{.}}\)
\(EC = 5\;{\rm{cm}}{\rm{.}}\)
Chu vi \(\Delta DEC\) lớn hơn \(12\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 5\;{\rm{cm,}}\;AC = 12\;{\rm{cm}}{\rm{.}}\) Gọi \(AD\) là đường cao của \(\Delta ABC.\)
\(BC = 13\;{\rm{cm}}{\rm{.}}\)
Diện tích \(\Delta ABC\) bằng \(60\;{\rm{c}}{{\rm{m}}^2}.\)
\(AD = 4,5\;{\rm{cm}}{\rm{.}}\)
\(\widehat B > \widehat {DAB}.\)
Cho \(\Delta ABC\) vuông tại \(A\) có \(BC = 52\;{\rm{cm,}}\;\frac{{AB}}{{AC}} = \frac{5}{{12}}.\) Chu vi của \(\Delta ABC\) bằng bao nhiêu centimet?
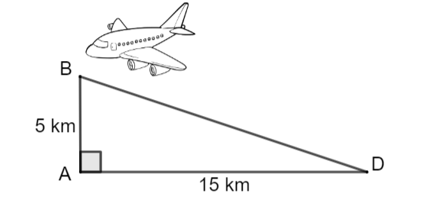
Một máy bay ở độ cao \(5\;{\rm{km}}{\rm{.}}\) Khoảng cách từ hình chiếu vuông góc của máy bay xuống mặt đất (vị trí \(A\)) đến vị trí \(D\) của sân bay là \(15\;{\rm{km}}\) (Hình vẽ). Hỏi khoảng cách từ vị trí máy bay đến vị trí \(D\) của sân bay là bao nhiêu \({\rm{km?}}\)(Làm tròn kết quả đến hàng đơn vị)
Cho tam giác \(ABC\) đều có độ dài cạnh bằng \(30\;{\rm{cm}}{\rm{.}}\) Tính chiều cao của tam giác đó (Đơn vị: \({\rm{cm}}\)). (Làm tròn kết quả đến hàng đơn vị)
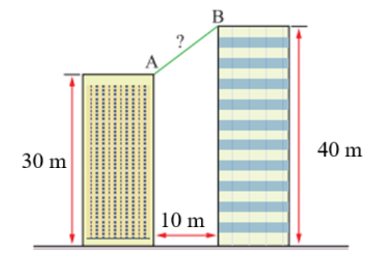
Khoảng cách giữa hai điểm \(A\) và \(B\) trong hình vẽ bằng bao nhiêu mét? (Làm tròn kết quả đến hàng phần mười của mét).
Cho hình vẽ sau:
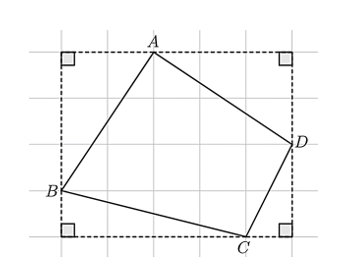
Biết rằng độ dài cạnh mỗi ô vuông bằng \(1\;{\rm{cm}}{\rm{.}}\) Chu vi tứ giác \(ABCD\) bằng bao nhiêu \({\rm{cm}}?\) (Làm tròn kết quả đến hàng phần mười).




