20 câu trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn, yêu cầu chọn phương án đúng nhất)
Biểu thức nào sau đây là đơn thức?
\(2{x^2}y.\)
\(2{x^2} + y.\)
\({x^2} + 2y.\)
\(2x + {y^2}.\)
Đơn thức nào sau đây là đơn thức thu gọn
\(3xy{x^2}\).
\(3xyz.y.\)
\(3xyz.z.\)
\(3{x^2}yz.\)
Đơn thức \(6{x^2}{y^2}z\) có hệ số là
\(6.\)
\(2.\)
\(5.\)
\(\frac{1}{6}.\)
Đơn thức \(6{x^2}{y^2}z\) có bậc là
\(6.\)
\(2.\)
\(5.\)
\(3.\)
Đơn thức đồng dạng với đơn thức \(2xyz\) là
\(3xyz.\)
\(3{x^3}{y^2}z.\)
\(3{x^2}{y^2}z.\)
\(2{x^2}{y^2}{z^2}.\)
Kết quả của phép cộng \(2{x^2}y + 3{x^2}y\) là
\(6{x^2}y.\)
\(5{x^2}y.\)
\(5{x^4}{y^2}.\)
\(6{x^4}{y^2}.\)
Kết quả của \(6x{y^2} - 2x{y^2}\) là
\(4x{y^2}.\)
\(8x{y^2}.\)
\(3x{y^2}.\)
\(4{x^2}y.\)
Cho đơn thức \(A = \left( { - 2} \right){x^2}y.\left( { - 0,5} \right){y^2}z\). Giá trị của biểu thức tại \(x = 4,y = 0,5\) và \(z = 2\) là
\(2.\)
\(4.\)
\( - 4.\)
\( - 2.\)
Chọn phát biểu sai trong các phát biểu dưới đây.
Mỗi số khác 0 là một đơn thức thu gọn bậc 0.
Hai đơn thức đồng dạng thì cùng bậc.
Hai số khác 0 cũng được coi là đơn thức đồng dạng.
Số 0 không là đơn thức.
Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước (tính bằng mét) được ghi trên đó.
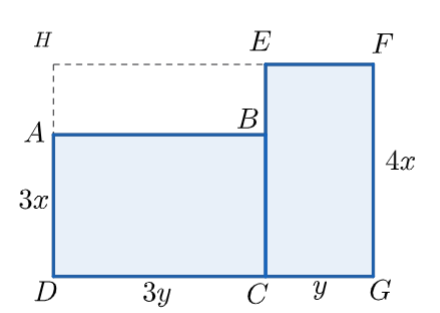
Hãy tìm đơn thức (thu gọn) với hai biến \(x,y\) biểu thị mảnh đất đã cho.
\(9xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\(16xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\(4xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\(13xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, mỗi câu hỏi có 4 ý khẳng định, yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định)
Cho biểu thức \(P = 2018x{y^2} + 16x{y^2} - 2016x{y^2}\).
a)Thu gọn được biểu thức \(P = 18x{y^2}\).
b)Hệ số của biểu thức \(P\) thu gọn là \(18.\)
c)Biểu thức \(P\) là một đơn thức bậc \(2.\)
d)Giá trị của biểu thức \(P\) tại \(x = 2,y = \frac{1}{2}\) lớn hơn \(10.\)
Trong homestay Panorama Tam Đảo (Vĩnh Phúc) có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có độ sâu \(1,4{\rm{ }}\left( {\rm{m}} \right){\rm{,}}\) đáy là hình chữ nhật có chiều dài \(x{\rm{ }}\left( {\rm{m}} \right),\) chiều dài \(y{\rm{ }}\left( {\rm{m}} \right)\). Bể thứ hai có độ sâu \(1,6{\rm{ }}\left( {\rm{m}} \right)\), đáy là hình chữ nhật có diện tích gấp 3 lần diện tích đáy của bể thứ nhất. Người ta bơm nước vào đầy hai bể bơi.
a)Thể tích của bể bơi thứ nhất là \(1,4xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
b)Diện tích đáy của bể bơi thứ hai là \(3xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
c)Thể tích của bể bơi thứ hai lớn hơn \(5xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
d)Cần nhiều hơn \(6xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\) nước để bơm đầy vào hai bể bơi trong homestay.
Một bức tường hình thang có cửa số hình tròn với các kích thước như hình dưới đây. (Đơn vị: mét, lấy \(\pi = 3,14\))
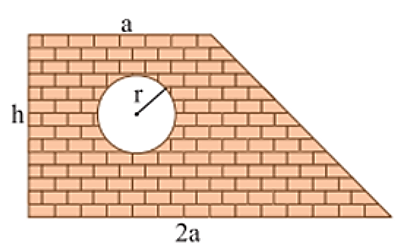
a)Diện tích toàn bộ bức tường là \(\frac{{3a.h}}{2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
b)Diện tích phần cửa kính hình tròn là \(2\pi {r^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
c)Biểu thức biểu thị diện tích bức tường không tính phần cửa sổ là \(S = \frac{{3a.h}}{2} - 2\pi {r^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d)Khi \(a = 2{\rm{ }}\left( {\rm{m}} \right){\rm{, }}h = 3{\rm{ }}\left( {\rm{m}} \right){\rm{, }}r = 0,5{\rm{ }}\left( {\rm{m}} \right)\) thì diện tích bức tường hình thang lớn hơn \({\rm{7 }}\left( {{{\rm{m}}^2}} \right).\)
Một mảnh vườn hình chữ nhật với chiều rộng là \(x{\rm{ }}\left( {\rm{m}} \right)\), chiều dài là \(y{\rm{ }}\left( {\rm{m}} \right)\) (với \(y > x > 0\)). Sau khi mở rộng mảnh vườn, ta có chiều rộng mới gấp hai lần chiều rộng ban đầu, chiều dài mới bằng \(\frac{3}{2}\) chiều dài ban đầu của mảnh vườn.
a)Diện tích ban đầu của mảnh vườn là \(xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
b)Chiều rộng mới của mảnh vườn khi mở rộng là \(2x{\rm{ }}\left( {\rm{m}} \right),\) chiều dài mới là \(\frac{3}{2}y{\rm{ }}\left( {\rm{m}} \right)\).
c)Diện tích của mảnh vườn sau khi mở rộng là \(3xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d)Diện tích phần được mở rộng thêm của mảnh vườn lớn hơn \(2xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Cho biểu thức \(B = \frac{{ - 3}}{2}{x^3}{y^2}x.\left( { - 6} \right)x{y^3}{z^5}\).
a)Thu gọn đơn thức được \(B = 9{x^4}{y^5}{z^6}\).
b)Đơn thức có hệ số là 9.
c)Đơn thức \(B\) có bậc là \(15.\)
d)Giá trị của \(B = 9\) khi \(x = 1,y = - 1,z = - 1.\)
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, mỗi câu hỏi yêu cầu đưa ra đáp án là một con số, tối đa có 4 kí tự, tính cả kí tự dấu và kí tự dấu phẩy
Cho đơn thức \(F = {\left( {\frac{{ - 3}}{5}x{y^2}} \right)^2}.\left( {\frac{{20}}{9}{x^3}y} \right)\). Xác định hệ số của đơn thức trên sau khi thu gọn. (Kết quả ghi dưới dạng số thập phân)
Tính giá trị của đơn thức \(C = \frac{1}{3}.{\left( { - 6{x^2}y} \right)^2}.\left( {\frac{1}{2}{x^3}y} \right)\) tại \(x = 1,y = - 1\).
Cho các đơn thức sau: \(\sqrt 5 ;{\rm{ }}{x^2};{\rm{ }}\frac{{{5^2}}}{{98}}{y^4};{\rm{ }} - \sqrt 7 x{y^2}{z^3}y;{\rm{ }}\frac{{\sqrt 2 }}{{11}}xy{z^2}z.\) Có bao nhiêu đơn thức không là đơn thức thu gọn?
Xác định hệ số của đơn thức \(M,\) biết: \(2{x^4}{y^3} + M = - 3{x^4}{y^3}\).
Xác định bậc của đơn thức \(A = - 4{a^2}x.{\left( { - 2bxy} \right)^2}.\left( { - \frac{1}{4}{x^2}{y^3}} \right)\) với \(a,b\) là hằng số.





