20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1. Đơn thức và đa thức nhiều biến (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Biểu thức nào sau đây là đơn thức?
\(2{x^2}y.\)
\(2{x^2} + y.\)
\({x^2} + 2y.\)
\(2x + {y^2}.\)
Đơn thức nào sau đây là đơn thức thu gọn
\(3xy{x^2}\).
\(3xyz \cdot y.\)
\(3xyz \cdot z.\)
\(3{x^2}yz.\)
Đơn thức \(6{x^2}{y^2}z\) có bậc là
\(6.\)
\(2.\)
\(5.\)
\(3.\)
Biểu thức nào sau đây là đa thức?
\(\frac{3}{{2x}} + 3{y^2}.\)
\(4x + \frac{1}{y}.\)
\( - 2x + \frac{2}{{5x}}y.\)
\(\frac{3}{2}x + 4y.\)
Đa thức \(A = 5{x^3}y + 2xy - 3x\) có bậc là
4.
5.
7.
3.
Thu gọn đa thức \(\left( {xy + {y^2} - {x^2}{y^2} - 2} \right) + \left( {{x^2}{y^2} + 5 - {y^2}} \right)\) được
\(xy + 3.\)
\(xy - 3.\)
\( - xy + 3.\)
\( - xy - 3.\)
Đa thức thu gọn trong các đa thức dưới dây là
\(\frac{1}{3}{x^2}y - xyz - {x^2}y.\)
\(\frac{1}{3}{x^2}y - xyz - zxy.\)
\( - 2x{y^2} + \frac{2}{5}y - 4{y^2}x.\)
\(\frac{3}{2}x{y^2} + 3{y^2}.\)
Cho đơn thức \(A = \left( { - 2} \right){x^2}y.\left( { - 0,5} \right){y^2}z\). Giá trị của biểu thức tại \(x = 4,y = 0,5\) và \(z = 2\) là
\(2.\)
\(4.\)
\( - 4.\)
\( - 2.\)
Tính giá trị của đa thức \(C = xy + {x^2}{y^2} + {x^3}{y^3} + ... + {x^{100}}{y^{100}}\) tại \(x = - 1,y = - 1\).
\(C = 10.\)
\(C = 99.\)
\(C = 100.\)
\(C = 1{\rm{ }}000.\)
Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước (tính bằng mét) được ghi trên đó.
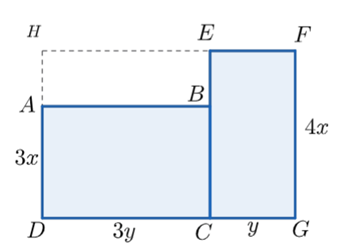
Hãy tìm đơn thức (thu gọn) với hai biến \(x,y\) biểu thị mảnh đất đã cho.
\(9xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\(16xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\(4xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
\(13xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Phần II. Trắc nghiệm đúng, sai
Cho biểu thức \(P = 2018x{y^2} + 16x{y^2} - 2016x{y^2}\).
a) Thu gọn được biểu thức \(P = 18x{y^2}\).
b) Hệ số của biểu thức \(P\) thu gọn là \(18.\)
c) Biểu thức \(P\) là một đơn thức bậc \(2.\)
d) Giá trị của biểu thức \(P\) tại \(x = 2,y = \frac{1}{2}\) lớn hơn \(10.\)
Trong homestay Panorama Tam Đảo (Vĩnh Phúc) có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có độ sâu \(1,4{\rm{ }}\left( {\rm{m}} \right){\rm{,}}\) đáy là hình chữ nhật có chiều dài \(x{\rm{ }}\left( {\rm{m}} \right),\) chiều dài \(y{\rm{ }}\left( {\rm{m}} \right)\). Bể thứ hai có độ sâu \(1,6{\rm{ }}\left( {\rm{m}} \right)\), đáy là hình chữ nhật có diện tích gấp 3 lần diện tích đáy của bể thứ nhất. Người ta bơm nước vào đầy hai bể bơi.
a) Thể tích của bể bơi thứ nhất là \(1,4xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
b) Diện tích đáy của bể bơi thứ hai là \(3xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
c) Thể tích của bể bơi thứ hai lớn hơn \(5xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
d) Cần nhiều hơn \(6xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\) nước để bơm đầy vào hai bể bơi trong homestay.
Cho đa thức \(A = 6{x^2}y + 50,5x{y^2} + {x^2}y - 51,5x{y^2}.\)
a) Thu gọn đa thức \(A = 7{x^2}y - x{y^2}.\)
b) Các hạng tử trong đa thức \(A\) đều có bậc là 3.
c) Đa thức \(A\) có bậc là 3.
d) Giá trị của \(A = - 16\) khi \(x = 1;y = - 2\).
Một mảnh vườn hình chữ nhật với chiều rộng là \(x{\rm{ }}\left( {\rm{m}} \right)\), chiều dài là \(y{\rm{ }}\left( {\rm{m}} \right)\) (với \(y > x > 0\)). Sau khi mở rộng mảnh vườn, ta có chiều rộng mới gấp hai lần chiều rộng ban đầu, chiều dài mới bằng \(\frac{3}{2}\) chiều dài ban đầu của mảnh vườn.
a) Diện tích ban đầu của mảnh vườn là \(xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
b) Chiều rộng mới của mảnh vườn khi mở rộng là \(2x{\rm{ }}\left( {\rm{m}} \right),\) chiều dài mới là \(\frac{3}{2}y{\rm{ }}\left( {\rm{m}} \right)\).
c) Diện tích của mảnh vườn sau khi mở rộng là \(3xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d) Diện tích phần được mở rộng thêm của mảnh vườn lớn hơn \(2xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Cho đa thức \(A = 2{x^2}y + {x^2} + {y^2} + xy - 2{x^2}y;B = - 3xy\) và \(C = A + B\).
a) Thu gọn đa thức \(A\), ta được \(A = {x^2} + xy + {y^2}\).
b) Bậc của đa thức \(A\) là 3.
c) Thu gọn đa thức \(C\), ta được \(C = {x^2} + {y^2}\).
d) Giá trị của đa thức \(C = A + B\) tại \(x = 24\) và \(y = 25\) là 1.
Phần III. Trắc nghiệm trả lời ngắn
Cho \(P = xyz + {x^2}{y^2}{z^2} + {x^3}{y^3}{z^3} + ... + {x^{2020}}{y^{2020}}{z^{2020}}\). Tính giá trị của \(P\) khi biết \(x = 1;y = 1;\)\(z = - 1\).
Tính giá trị của đơn thức \(C = \frac{1}{3}.{\left( { - 6{x^2}y} \right)^2}.\left( {\frac{1}{2}{x^3}y} \right)\) tại \(x = 1,y = - 1\).
Tính giá trị của đa thức \(B = 3{x^5}{y^3} - 4{x^4}{y^3} + 2{x^4}{y^3} - 3{x^5}{y^3}\) tại \(x = 1;y = - 2.\)
Tính giá trị của đa thức \(N = 3{x^4} + 5{x^2}{y^2} + 2{y^4} + 2{y^2}\) biết rằng \({x^2} + {y^2} = 2.\)
Xác định bậc của đơn thức \(A = - 4{a^2}x \cdot {\left( { - 2bxy} \right)^2} \cdot \left( { - \frac{1}{4}{x^2}{y^3}} \right)\) với \(a,b\) là hằng số.

