20 câu trắc nghiệm Toán 8 Cánh diều Bài 5. Phân thức đại số (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, hãy chọn phương án đúng duy nhất)
Biểu thức nào không phải là phân thức đại số?
\(\frac{x}{{x - 2}}.\)
\(\frac{{{y^2}}}{{\left( {x - 2} \right)x}}.\)
\(x.\)
\(\frac{y}{{\frac{1}{{{x^2}}}}}.\)
Hai phân thức \(\frac{A}{B} = \frac{M}{N}\) nếu
\(A \cdot B = C \cdot D.\)
\(A \cdot N = B \cdot M.\)
\(A \cdot M = B \cdot N.\)
\(A \cdot B = M \cdot N.\)
Phân thức nào dưới đây bằng với phân thức \(\frac{{3xy}}{4}\)?
\(\frac{{6{x^2}{y^2}}}{{ - 8xy}}.\)
\(\frac{{9{x^2}{y^2}}}{{12{x^2}y}}.\)
\(\frac{{15{x^2}{y^2}}}{{20xy}}.\)
\(\frac{{15{x^3}{y^3}}}{{20}}.\)
Phân thức nào dưới đây bằng với phân thức \(\frac{{2{x^3}{y^2}}}{5}\)?
\(\frac{{14{x^3}{y^4}}}{{35xy}}.\)
\(\frac{{14{x^4}{y^3}}}{{5xy}}.\)
\(\frac{{14{x^4}{y^3}}}{{35}}.\)
\(\frac{{14{x^4}{y^3}}}{{35xy}}.\)
Khẳng định nào sau đây là sai?
\(\frac{A}{B} = \frac{{A.M}}{{B.M}}\), \(M\) là một đa thức khác đa thức 0.
\(\frac{A}{B} = \frac{{A + M}}{{B + M}}.\)
\(\frac{A}{B} = \frac{{A:N}}{{B:N}},\)\(N\) là một nhân tử chung của \(A\) và \(B\).
\(\frac{A}{B} = - \frac{{ - A}}{{ - B}}.\)
Chọn đáp án đúng. Với đa thức \(B\) khác đa thức 0 thì
\(\frac{A}{B} = \frac{{ - A}}{{ - B}}.\)
\(\frac{A}{B} = \frac{A}{{ - B}}.\)
\(\frac{A}{B} = \frac{{ - A}}{B}.\)
\(\frac{A}{B} = - \frac{{ - A}}{{ - B}}.\)
Áp dụng quy tắc đổi dấu để viết phân thức bằng phân thức \(\frac{5}{{{y^2} - {x^2}}}\), ta được
\(\frac{5}{{{x^2} - {y^2}}}.\)
\(\frac{{ - 5}}{{{x^2} - {y^2}}}.\)
\(\frac{5}{{{x^2} + {y^2}}}.\)
\(\frac{{ - 5}}{{{x^2} + {y^2}}}.\)
Điều kiện xác định của phân thức \(\frac{{x - 1}}{{x - 2}}\) là
\(x \le 2.\)
\(x \ne 1.\)
\(x = 2.\)
\(x \ne 2.\)
Kết quả rút gọn của phân thức \(\frac{{14{x^3}{y^2}}}{{21x{y^6}}}\) là
\(\frac{{2{x^3}}}{{3{y^3}}}.\)
\(\frac{{2{x^2}}}{{3{y^4}}}.\)
\(\frac{2}{3}.\)
\(\frac{{2{x^2}{y^4}}}{{3y}}.\)
Mẫu thức chung của hai phân thức \(\frac{{3x}}{{{x^2} - 4}}\) và \(\frac{x}{{x + 2}}\) là
\({x^2} - 4.\)
\(x + 2.\)
\(\left( {{x^2} - 4} \right)\left( {x + 2} \right).\)
\(x - 2.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d))
Cho hình chữ nhật \(ABCD\) và hình vuông \(EFGH\) như hình bên dưới.
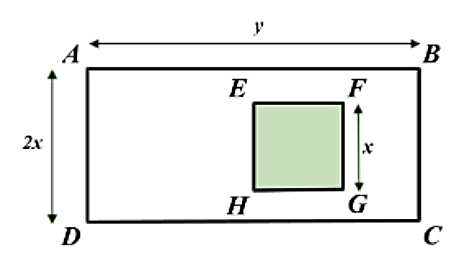
a)Diện tích hình vuông \(EFGH\) là \({x^2}\), diện tích hình chữ nhật \(ABCD\) là \(2xy\).
b)Biểu thức biểu diễn tỉ số diện tích hình vuông và diện tích hình chữ nhật là \(T = \frac{{2y}}{x}.\)
c)Điều kiện xác định của tỉ số diện tích hình vuông và diện tích hình chữ nhật là \(x \ne 0.\)
d)Giá trị của phân thức biểu diễn tỉ số diện tích hình vuông và diện tích hình chữ nhật tại
\(x = 2,y = 8\) là \(\frac{1}{8}.\)
Một vườn cây có \({x^2} + 2x - {y^2} - 2y\)cây, trong đó có \({x^2} - {y^2}\) cây lấy gỗ, còn lại là cây ăn quả.
a)Số cây ăn quả trong vườn là \(2\left( {x + y} \right)\) cây.
b)Biểu thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả là \(2\left( {x - y} \right)\) cây.
c)Biểu thức biểu thị tỉ số cây lấy gỗ và số cây có trong vườn là \(\frac{1}{{2x - 2y}}\).
d)Biểu thức biểu thị tỉ số cây ăn quả và số cây có trong vườn là \(\frac{2}{{x + y + 2}}.\)
Chị Hà mở một xưởng thủ công với vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc,…) là 80 triệu. Biết chi phí để sản xuất (tiền mua vật liệu, lương nhân công) của một sản phẩm là 15 nghìn đồng. Gọi \(x\) là số sản phẩm mà xưởng chị Hà làm được.
a)Chi phí để sản xuất ra \(x\) sản phẩm là \(15x\) (nghìn đồng).
b)Chi phí thực đã bỏ ra để làm được \(x\) sản phẩm là \(80 + 15x\) (nghìn đồng).
c)Chi phí thực đã bỏ ra để tạo ra một sản phẩm theo \(x\) là \(\frac{{80 + 15x}}{x}\) (nghìn đồng).
d)Với \(x = 1{\rm{ }}000\) thì chi phí thực để tạo ra một sản phẩm sẽ lớn hơn \(100\) (nghìn đồng).
Lúc 6 giờ sáng, bác Vinh lái ô tô xuất phát từ Hà Nội đi huyện Tỉnh Gia (Thanh Hóa). Khi đến Phủ Lý (Hà Nam), cách Hà Nội khoảng 60 km, bác Vinh dừng lại ăn sáng trong 20 phút. Sau đó, bác Vinh tiếp tục đi về Tĩnh Gia và phải tăng vận tốc thêm 10 km/h để đến nơi đúng giờ dự định. Biết rằng, quãng đường Hà Nội – Tĩnh Gia có chiều dài khoảng 200 km. Gọi \(x\) (km/h) là vận tốc ô tô đi trên quãng đường Hà Nội – Phủ Lý.
a)Thời gian bác Vinh chạy trên quãng đường Hà Nội – Phủ Lý là \(\frac{{60}}{x}\) (giờ).
b)Quãng đường từ Phủ Lý đến Tĩnh Gia là 140 km.
c)Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý – Tĩnh Gia là \(\frac{{140}}{{x - 10}}\) (giờ).
d)Bác Vinh đến Tĩnh Gia vào lúc 9 giờ 20 phút khi ô tô đi với vận tốc 60 km/h trên quãng đường Hà Nội – Phủ Lý.
Cho biểu thức \(C = \frac{{{x^3} + {x^2} - 2x}}{{x\left( {x + 2} \right) - {x^2} + 4}}\).
a)Điều kiện xác định của \(C\) là \(x \ne 2,x \ne - 2\).
b)Rút gọn được \(C = \frac{{x\left( {x - 1} \right)}}{2}\).
c)Giá trị của biểu thức \(C\) tại \(x = \frac{1}{2}\) là \( - \frac{1}{8}.\)
d)Biểu thức \(C\)có giá trị nguyên khi \(x \in \mathbb{Z}\).
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Giá trung bình của một chiếc áo sơ mi được một xí nghiệp sản xuất cho bởi biểu thức \(C\left( x \right) = \frac{{0,002{x^2} + 120x + 1000}}{x}\) , trong đó \(x\) là số áo được sản xuất và \(C\) tính bằng nghìn đồng. Tính giá trị của \(C\) khi \(x = 1000.\)
Để loại bỏ \(x\) (tính theo %) chất gây ô nhiễm không khí từ khí thải của một nhà máy, ước tính chi phí cần là \(\frac{{1,7x}}{{100 - x}}\) (tỉ đồng). Nếu muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là bao nhiêu tỉ đồng?
Biết \(x > y > 0\) và \(3{x^2} + 3{y^2} = 10xy\). Tính giá trị của \(P = \frac{{y - x}}{{y + x}}\). (Kết quả ghi dưới dạng số thập phân)
Cho hình chữ nhật \(ABCD\) và \(MNPQ\) như hình vẽ (các số đo trên hình tính theo đơn vị centimet)
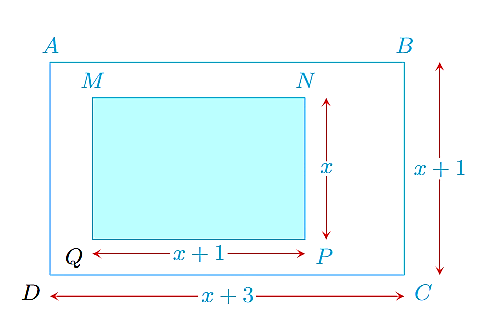
Biết rằng \(T\) là tỉ số diện tích của hình chữ nhật \(ABCD\) và hình chữ nhật \(MNPQ\). Tính giá trị của \(T\) tại \(x = 5.\) (Kết quả ghi dưới dạng số thập phân)
Tìm giá trị lớn nhất của phân thức \(A = \frac{1}{{{x^2} + 2x + 5}}\).

