20 câu trắc nghiệm Toán 8 Cánh diều Bài 4. Vận dụng các hằng đẳng thức đáng nhớ vào phân tích đa thức thành nhân tử (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phân tích đa thức thành nhân tử \({x^2}{y^2}z + x{y^2}{z^2} + {x^2}y{z^2}\) ta được
\(x\left( {x{y^2}z + {y^2}{z^2} + xy{z^2}} \right)\).
\(y\left( {{x^2}yz + xy{z^2} + {x^2}{z^2}} \right).\)
\(z\left( {x{y^2} + x{y^2}z + {x^2}yz} \right).\)
\(xyz\left( {xy + yz + xz} \right).\)
Kết quả phân tích đa thức \({x^2} - xy + x - y\) thành nhân tử là
\(\left( {x + 1} \right)\left( {x - y} \right)\).
\(\left( {x - y} \right)\left( {x - 1} \right).\)
\(\left( {x - y} \right)\left( {x + y} \right).\)
\(x\left( {x - y} \right).\)
Phân tích đa thức\({x^3} - 4x\) thành nhân tử, ta được
\(x\left( {{x^2} + 4} \right).\)
\(x\left( {x + 2} \right)\left( {x - 2} \right).\)
\({x^2}\left( {x - 4} \right).\)
\(x\left( {x + 4} \right)\left( {x - 4} \right).\)
Phân tích đa thức \({\left( {x - 4} \right)^2} + \left( {x - 4} \right)\) thành nhân tử, ta được:
\(\left( {x - 4} \right)\left( {x - 3} \right).\)
\(\left( {x - 4} \right)\left( {x - 5} \right).\)
\(\left( {x + 4} \right)\left( {x + 3} \right).\)
\(\left( {x + 4} \right)\left( {x - 4} \right).\)
Phân tích đa thức \({x^2} - 6x + 8\) thành nhân tử, ta được:
\(\left( {x - 4} \right)\left( {2 - x} \right).\)
\(\left( {x - 4} \right)\left( {x + 2} \right).\)
\(\left( {x - 4} \right)\left( {x - 2} \right).\)
\(\left( {x + 4} \right)\left( {x - 4} \right).\)
Phân tích đa thức \(8{x^3} - 12{x^2}y + 6x{y^2} - {y^3}\) thành nhân tử, ta được:
\({\left( {2x - y} \right)^3}.\)
\( - {\left( {2x + y} \right)^3}.\)
\({\left( {2x + y} \right)^3}.\)
\({\left( {x - 2y} \right)^3}.\)
Chọn khẳng định đúng trong các khẳng định dưới đây:
\(27 + 27x + 9{x^2} + {x^3} = {\left( {3 + x} \right)^3}.\)
\({x^3} - 3{x^2} + 3x - 1 = {\left( {1 - x} \right)^3}.\)
\(1 - 2y + {y^2} = - {\left( {y - 1} \right)^2}.\)
\(1 - {x^2}{y^4} = - \left( {1 - x{y^2}} \right)\left( {x + x{y^2}} \right)\).
Phân tích đa thức \({x^4} - 16\) thành nhân tử, ta được:
\(\left( {{x^2} + 4} \right)\left( {{x^2} - 4} \right).\)
\(\left( {{x^2} + 4} \right)\left( {x - 2} \right)\left( {x + 2} \right).\)
\(\left( {{x^2} + 4} \right)\left( {{x^2} - 2} \right).\)
\(\left( {{x^2} - 4} \right)\left( {x - 2} \right)\left( {{x^2} + 2} \right).\)
Phân tích đa thức \({x^3} - 9{x^2} + 27x - 27\) thành nhân tử ta được kết quả là
\({\left( {x + 9} \right)^3}.\)
\({\left( {x + 3} \right)^3}.\)
\({\left( {x - 9} \right)^3}.\)
\({\left( {x - 3} \right)^3}.\)
Phân tích đa thức \({x^2} - {y^2} + 2y - 1\) thành nhân tử ta được kết quả là
\(\left( {x + y + 1} \right)\left( {x - y - 1} \right).\)
\(\left( {x - y - 1} \right)\left( {x + y - 1} \right).\)
\(\left( {x + y + 1} \right)\left( {x + y - 1} \right).\)
\(\left( {x - y + 1} \right)\left( {x + y - 1} \right).\)
Một mảnh vườn hình vuông có độ dài cạnh bằng \(x\) (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng \(y\) (mét).
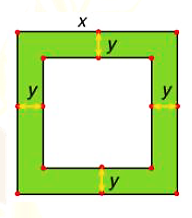
a) Diện tích của cả mảnh vườn là \({x^2}\) (m2).
b) Diện tích phần đất không làm lối đi là \({y^2}\) (m2).
c) Diện tích phần đất làm đường đi là \(S = {x^2} - 2{y^2}\) (m2).
d) Diện tích phần đất làm đường lớn hơn 2 000 m2 khi \(x = 48{\rm{ m, }}y = 2{\rm{ m}}{\rm{.}}\)
Từ một miếng bìa có dạng hình tròn bán kính \(R\) (cm), bạn Hạnh khoét một hình tròn ở giữa có bán kính \(r\) (cm), \(\left( {0 < r < R} \right)\). Lấy \(\pi = 3,14.\)
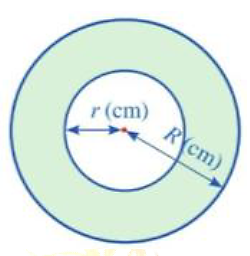
a) Diện tích miếng bìa hình tròn bán kính \(R\) cm là \(\pi {R^2}\) (cm2).
b) Diện tích miếng bìa hình tròn bán kính \(r\) cm là \(2\pi {r^2}\) (cm2).
c) Diện tích phần còn lại của miếng bìa là \(S = \pi {R^2} - 2\pi {r^2}\) (cm2).
d) Diện tích phần còn lại của miếng bìa lớn hơn \(181\) cm2 khi \(x = 8{\rm{ cm, }}y = 2,5{\rm{ cm}}{\rm{.}}\)
</>
Từ một sợi dây có dộ dài \(200{\rm{ cm,}}\) Hùng cắt ra thành hai đoạn dây, một đoạn lớn, một đoạn nhỏ, mỗi đoạn có độ dài theo centimet là một số tự nhiên chia hết cho 4. Hùng đặt hai đoạn dât trên mặt bàn sao cho mỗi đoạn dây tạo thành một hình cuông, hình vuông nhỏ nằm trong hình vuông lớn. Gọi độ dài đoạn dây lớn và nhỏ lần lượt được cắt ra là \(4x\) và \(4y\) \(\left( {x,y \in {\mathbb{N}^*},{\rm{ cm}}} \right)\).

a) Tổng độ dài hai cạnh hình vuông lớn và hình vuông nhỏ là 50 cm.
b) Diện tích phần nằm giữa hai hình vuông là \(S = 50\left( {x - y} \right){\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
c) Để diện tích phần nằm giữa hai hình vuông lớn nhất thì cạnh hình vuông lớn có độ dài là
49 cm, cạnh hình vuông nhỏ có độ dài là 1 cm.
d) Để diện tích phần nằm giữa hai hình vuông lớn nhất thì cắt sợi dây có độ dài thành hai đoạn 196 cm và 4 cm.
Một thử ruộng hình chữ nhật có chiều dài bằng \(20{\rm{ m}}\), chiều rộng bằng \(\frac{1}{2}\) chiều dài. Nếu giảm chiều dài đi \(x{\rm{ }}\left( {\rm{m}} \right)\) và tăng chiều rộng thêm \(x{\rm{ }}\left( {\rm{m}} \right)\).
a) Chiều rộng ban đầu của thửa ruộng là \(10{\rm{ }}\left( {\rm{m}} \right)\).
b) Diện tích của thửa ruộng sau khi thay đổi chiều dài, chiều rộng là \(\left( {20 - x} \right)\left( {10 + x} \right){\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
c) Sau khi giảm chiều dài đi \(x{\rm{ }}\left( {\rm{m}} \right)\) và tăng chiều rộng thêm \(x{\rm{ }}\left( {\rm{m}} \right)\) thì diện tích thửa ruộng không thể vượt quá \(225{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
d) Diện tích thửa ruộng sau khi thay đổi đạt giá trị lớn nhất khi \(x = 2{\rm{ }}\left( {\rm{m}} \right).\)
Bác An gửi tiết kiệm với số tiền 400 triệu đồng vào một ngân hàng, kì hạn 12 tháng và theo thể thức lãi kép (nghĩa là nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào làm vốn ban đầu để tính lãi cho năm tiếp theo). Giả sử lãi xuất cố định là \(x\% \)/năm, \(x > 0\). Biết rằng sau 2 năm gửi tiết kiệm, bác An nhận được số tiền gồm cả gốc lần lãi là \(449,44\) triệu đồng.
a) Số tiền cả gốc lần lãi của bác An sau năm thứ nhất là \(400 + 4x\) (triệu đồng).
b) Sau năm thứ hai thì số tiền cả gốc và lãi bác An có là \(\frac{{{x^2}}}{{25}} + 8x + 400\) (triệu đồng).
c) Vì sau hai năm gửi tiết kiệm, bác An nhận được số tiền gồm cả gốc lần lãi là \(449,44\) triệu đồng nên ta có \(\frac{{{x^2}}}{{25}} + 8x + 400 = 449,44\) (triệu đồng).
d) Lãi suất cố định mà bác An gửi nhỏ hơn \(5\% \).
Biết rằng \({x^2} - 2x - 3 = \left( {x - a} \right)\left( {x - b} \right)\). Khi đó, giá trị của \(a + b\) bằng bao nhiêu?
Cho biểu thức \(A = {x^4} - 2{x^2}y - {x^2} + {y^2} + y\) biết \({x^2} - y = 6\). Tính giá trị của biểu thức \(A\).
Biết rằng \({x^3} + {x^2} + 4 = \left( {x + a} \right)\left( {{x^2} - x + a} \right)\). Hỏi giá trị của \(a\) bằng bao nhiêu?
Cho \({\left( {x + y} \right)^3} - {\left( {x - y} \right)^3} = A \cdot y \cdot \left( {B{x^2} + C{y^2}} \right),\) biết \(A,B,C\) là các số nguyên tố. Khi đó \(A + B + C\) bằng bao nhiêu?
Biết rằng, tồn tại các số dương \(a,b\) thỏa mãn: \({a^3} + {b^3} + 8 = 6ab\). Tính giá trị \(a - b\).

