20 câu trắc nghiệm Toán 8 Cánh diều Bài 2. Các phép toán với đa thức nhiều biến (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Cho hai đa thức \(P = a + 3b + a{b^2}\) và \(Q = {a^2}b - a{b^2} - 2b\). Kết quả của \(P - Q\) là
\(a + b + {a^2}b.\)
\(a + 5b - {a^2}b + 2a{b^2}\)
\(a + b - {a^2}b.\)
\(a + 5b + {a^2}b + 2a{b^2}\).
Cho hai đa thức \(P\left( x \right) = {x^2} - 3x + 2\) và \(Q\left( x \right) = {x^2} + x - 2\). Kết quả \(P\left( x \right) - Q\left( x \right)\) là
\( - 4x - 4.\)
\(4x - 4.\)
\( - 4x + 4.\)
\(4x + 4.\)
Kết quả rút gọn biểu thức \(3x\left( {x - 5y} \right) + \left( {y - 5x} \right)\left( { - 3y} \right) - 3\left( {{x^2} - {y^2}} \right) - 1\) là
3.
0.
\(1.\)
\( - 1.\)
Trong các phép tính sau, phép tính nào có kết quả \(3{x^2} + 3{y^2}\)?
\(3x\left( {x + y} \right).\)
\(x\left( {x + y + 1} \right) - 3y\left( {x + y} \right) - x.\)
\(3x\left( {x + y} \right) - 3y\left( {x + y} \right).\)
\(3x\left( {y + x} \right) + y\left( { - 3x + 3y} \right).\)
Cho biểu thức \(C = x\left( {y + z} \right) - y\left( {z + x} \right) - z\left( {x - y} \right).\) Chọn khẳng định đúng.
Biểu thức \(C\) không phụ thuộc vào \(x;y;z.\)
Biểu thức \(C\) phụ thuộc vào \(x;y;z.\)
Biểu thức \(C\) chỉ phụ thuộc vào \(y.\)
Biểu thức \(C\) chỉ phụ thuộc vào \(z.\)
Kết quả của phép tính \(\left( {2{x^2}y + 4{x^2}{y^2}} \right):2xy\) bằng
\(x + 4xy.\)
\(x + 2xy.\)
\(2x + 4xy.\)
\(x + 4y.\)
Kết quả của phép chia \(\left( {4{x^2}{y^3} - \frac{1}{2}{x^2}y + x{y^2}} \right):\left( { - 2xy} \right)\) là
\( - 2x{y^2} + \frac{1}{4}x - \frac{1}{2}y.\)
\( - 2x{y^2} - \frac{1}{4}x + \frac{1}{2}y.\)
\( - 2xy + \frac{1}{4}x + \frac{1}{2}y.\)
\(2x{y^2} + \frac{1}{4}x + \frac{1}{2}y.\)
Bác Nam có một chiếc két sắt hình hộp chữ nhật với thể tích là \(2{x^2}y - 3x{y^2} + 4xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\); chiều cao của két bằng \(2y{\rm{ }}\left( {\rm{m}} \right)\). Diện tích đáy của chiếc két đó là
\({x^2} - \frac{3}{2}xy + 2x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
\({x^2} + \frac{3}{2}xy + 2x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
\( - {x^2} - \frac{3}{2}xy - 2x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
\({x^2} - 3xy + 2x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Một cửa hàng buổi sáng bán được \(8{x^3}y + 5{x^6}{y^5} - 3{x^5}{y^4}\) (bao gạo), buổi chiều bán được \({x^6}{y^5} - {x^5}{y^4}\) (bao gạo). Tính số bao gạo mà cửa hàng bán được trong một ngày.
\(8{x^3}y + 6{x^6}{y^5} - 4{x^5}{y^4}.\)
\(8{x^3}y + 6{x^6}{y^5}.\)
\(8{x^3}y + 5{x^6}{y^5} - 4{x^5}{y^4}.\)
\(6{x^6}{y^5} - 4{x^5}{y^4}.\)
Cho \(\left( {B + 2{x^2}{y^3}} \right).\left( { - 3xy} \right) = - 3{x^2}{y^2} - 6{x^3}{y^4}\). Khẳng định đúng là
\(B = xy + 2{x^2}{y^3}.\)
\(B = xy - 2{x^2}{y^3}.\)
\(B = xy + 4{x^2}{y^3}.\)
\(B = xy\).
Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là \(1,2{\rm{ m,}}\) đáy là hình chữ nhật có chiều dài là \(x\) mét, chiều rộng là \(y\) mét. Bể thứ hai có chiều sâu là \(1,5{\rm{ m,}}\) hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.
a) Cần bơm \(1,2xy{\rm{ }}{{\rm{m}}^3}\) nước để bơm đầy bể bơi thứ nhất.
b) Cần bơm \({\rm{7,5}}xy{\rm{ }}{{\rm{m}}^3}\) nước để bơm đầy bể bơi thứ hai.
c) Để bơm đầy cả hai bể cần \({\rm{8,9}}xy{\rm{ }}{{\rm{m}}^3}\) nước.
d) Lượng nước bơm đầy hai bể lớn hơn \(500{\rm{ }}{{\rm{m}}^3}\) khi \(x = 5{\rm{ m, }}y = 3{\rm{ m}}{\rm{.}}\)
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) và \(y{\rm{ }}\left( {\rm{m}} \right)\) như hình dưới đây. Lấy \(\pi = 3,14\).
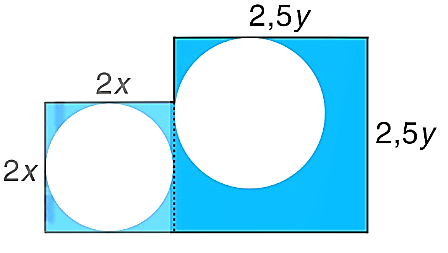
a) Tổng diện tích hai hình vuông là \(4{x^2} + 6,25{y^2}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
b) Tổng diện tích hai phần hình tròn là \(2\pi \left( {{x^2} + {y^2}} \right){\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
c) Biểu thức biểu thị diện tích phần còn lại của miếng bìa là \(\left( {4 - 2\pi } \right){x^2} + \left( {6,25 - 2\pi } \right){y^2}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
d) Diện tích phần còn lại của miếng bìa lớn hơn \({\rm{30 }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\) khi \(x = 2{\rm{ cm, }}y = {\rm{3 cm}}{\rm{.}}\)
Từ một miếng bìa hình chữ nhật có chiều dài là \(x{\rm{ }}\left( {{\rm{cm}}} \right)\), chiều rộng là \(x - 4{\rm{ }}\left( {{\rm{cm}}} \right)\). Người ta cắt bốn hình vuông cạnh \(2{\rm{ }}\left( {{\rm{cm}}} \right)\) ở bốn góc của miếng bìa rồi gấp lại để tạo thành một hình hộp chữ nhật không nắp như hình vẽ dưới đây.
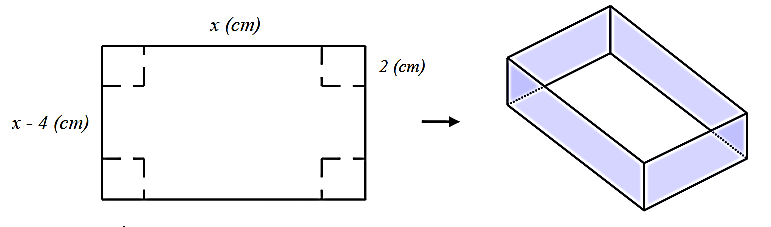
a) Chiều dài của chiếc hộp là \(x - 4{\rm{ }}\left( {{\rm{cm}}} \right)\), chiều rộng của chiếc hộp là \(x - 8{\rm{ }}\left( {{\rm{cm}}} \right)\).
b) Đa thức biểu thị thể tích của chiều hộp là \(2{x^2} - 24x + 64{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
c) Đa thức biểu thị diện tích xung quanh của chiếc hộp là \(8\left( {x - 2} \right){\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
d) Tổng diện tích năm mặt của chiếc hộp là \({x^2} - 4x + 16{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Bác Quang có một mảnh đất hình vuông cạnh \(x{\rm{ }}\left( {\rm{m}} \right),\) bác muốn trồng hoa vào mảnh đất hình chữ nhật ở góc vườn (như hình vẽ). Biết diện tích trồng hoa là \(60{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
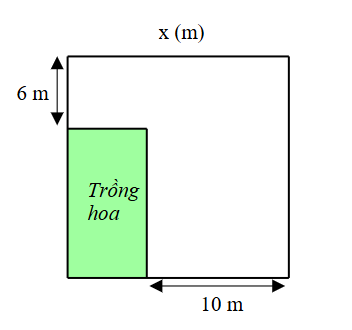
a) Diện tích mảnh đất hình vuông đó là \({x^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
b) Biểu thức biểu diễn diện tích phần đất trồng hoa là \(\left( {x - 6} \right)\left( {x - 10} \right){\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
c) Độ dài cạnh của mảnh đất hình vuông đó là \({\rm{15 }}\left( {\rm{m}} \right).\)
d) Diện tích phần còn lại của khu vườn lớn hơn \({\rm{185 }}\left( {{{\rm{m}}^2}} \right).\)
Một bể bơi có dạng hình hộp chữ nhật có chiều cao \(yz{\rm{ }}\left( {\rm{m}} \right)\), thể tích là \({x^2}{y^2}z + x{y^3}{z^2}{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Biết chiều rộng của đáy là \(xy{\rm{ }}\left( {\rm{m}} \right)\).
a) Diện tích đáy của bể bơi là \({x^2}y + x{y^2}z{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
b) Chiều dài của đáy bể bơi đó là \(x + z{\rm{ }}\left( {\rm{m}} \right)\).
c) Diện tích xung quanh của bể bơi đó là \(x{y^2}z + xyz + y{z^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d) Diện tích xung quanh của bể bơi có giá trị lớn hơn 40 \(\left( {{{\rm{m}}^2}} \right)\) khi \(x = 2;y = 1,z = 3\).
Một hình thang có đáy lớn bằng \(\left( {x + 2} \right)\) mét, đáy bé bằng \(\left( {x + 1} \right)\) mét và chiều cao bằng \(\left( {x + 3} \right)\) mét. Biết rằng tích độ dài đáy lớn và chiều cao hơn tích độ dài đáy bé và chiều cao là 4 mét. Tính diện tích của hình thang đó. (Đơn vị: mét vuông)
Cho ba số tự nhiên liên tiếp. Biết rằng tích của hai số sau lớn hơn tích của hai số đầu là 30. Hỏi số lớn nhất bằng bao nhiêu?
Biết rằng \(M + 3xy - 6{x^2}y = 3xy - \left( {9{x^2}y + 5xy} \right)\). Tính giá trị của \(M\) tại \(x = \frac{2}{3},y = - \frac{3}{4}.\)
Hai người đi xe đạp cùng một lúc và ngược chiều nhau từ hai địa điểm A và B. Người xuất phát từ A đi với vận tốc không đổi \(x{\rm{ }}\left( {{\rm{km/h}}} \right)\). Người xuất phát từ B đi với vận tốc không đổi \(y{\rm{ }}\left( {{\rm{km/h}}} \right)\). Hai người gặp nhau tại C sau 4 giờ. Tính quãng đường AB tại \(x = 10;y = 8\) (Đơn vị: km).
Có bao nhiêu số tự nhiên \(n\) để đa thức \(A = 20{x^7}{y^{2n}} - 10{x^4}{y^{3n}} + 7{x^5}{y^6}\) chia hết cho đơn thức \(B = {x^{n + 1}}{y^6}.\)

