20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 7. Thứ tự thực hiện các phép tính (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức không có dấu ngoặc?
Lũy thừa → Cộng và trừ → Nhân và chia.
Lũy thừa → Nhân và chia → Cộng và trừ.
Cộng và trừ → Nhân và chia → Lũy thừa.
Nhân và chia → Lũy thừa → Cộng và trừ.
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?
\[[] \to () \to \{ \} .\]
\[() \to [] \to \{ \} .\]
\[\{ \} \to [] \to ().\]
\[[] \to \{ \} \to ().\]
Kết quả của phép toán \[{2^{4\;}} - 50:25 + 13 \cdot 7\] là
100.
95.
105.
80.
Lập công thức tính thể tích của hình hộp chữ nhật dưới đây
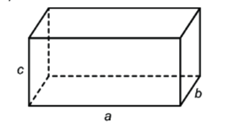
\(abc.\)
\(a + b + c.\)
\(\left( {a + b} \right)c.\)
\[\left( {a + b} \right){c^2}.\]
Dấu thích hợp điền vào chỗ chấm sau: \[{4^3} \ldots {10^2}-{6^2}\]
\( > .\)
\( < .\)
\( = .\)
\[ \ge .\]
Với \[a = 4\] thì giá trị của biểu thức \[a \cdot {5^2}--32:{a^2}\] bằng
98.
92.
32.
38.
Câu nào dưới đây là đúng khi nói đến giá trị của \[B = {3^2} \cdot \left[ {\left( {{5^2}\;--3} \right):11} \right]--{2^4}\; + 2 \cdot 10?\]
Kết quả có chữ số tận cùng là 3.
Kết quả là số lớn hơn 20.
Kết quả là số lớn hơn 30.
Kết quả là số lẻ.
Giá trị của \[x\] thỏa mãn \[105--3\left( {x--5} \right) = {3^5}:{3^2}\] là
37.
13.
31.
73.
Giá trị của biểu thức \[a--\left[ {45--{{\left( {6--1} \right)}^2}} \right] + {b^0}\] với \[a = 2026\] và \[b = 2025\] là
0.
2026.
2025.
2007.
Biểu thức tính diện tích hình chữ nhật ở hình dưới đây là
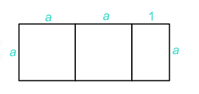
\[{a^2}.\]
\(2{a^2}.\)
\(\left( {a + 1} \right)a.\)
\(\left( {2a + 1} \right)a.\)
Cho số tự nhiên \(x\) thỏa mãn \[11x + 10 = 10 \cdot {3^2} + 5\left( {1 + 2 + 3} \right).\]
a) Biểu thức chỉ gồm các phép cộng, nhân, nâng lên lũy thừa và dấu ngoặc ta thực hiện trong ngoặc trước, ngoài ngoặc sau.
Cho số tự nhiên \(x\) thỏa mãn \[11x + 10 = 10 \cdot {3^2} + 5\left( {1 + 2 + 3} \right).\]
b) Giá trị của biểu thức \[10 \cdot {3^2} + 5\left( {1 + 2 + 3} \right)\] bằng 100.
Cho số tự nhiên \(x\) thỏa mãn \[11x + 10 = 10 \cdot {3^2} + 5\left( {1 + 2 + 3} \right).\]
c) Giá trị \(x\) thỏa mãn đề bài là \(x = 3\).
Cho số tự nhiên \(x\) thỏa mãn \[11x + 10 = 10 \cdot {3^2} + 5\left( {1 + 2 + 3} \right).\]
d) Với \(x = 4\) thì giá trị của biểu thức \[11x + 10\] bằng 54.
Trong một cuộc thi có 20 câu hỏi. Mỗi câu trả lời đúng được 10 điểm, mỗi câu trả lời sai bị trừ 3 điểm. Một học sinh đạt được 148 điểm.a) Bạn học sinh đó trả lời đúng tất cả các câu hỏi của cuộc thi.
Trong một cuộc thi có 20 câu hỏi. Mỗi câu trả lời đúng được 10 điểm, mỗi câu trả lời sai bị trừ 3 điểm. Một học sinh đạt được 148 điểm.
b) Khi bạn học sinh trả lời đúng 1 câu và trả lời sai 1 câu thì bạn ấy được 7 điểm.
Trong một cuộc thi có 20 câu hỏi. Mỗi câu trả lời đúng được 10 điểm, mỗi câu trả lời sai bị trừ 3 điểm. Một học sinh đạt được 148 điểm.
c) Bạn học sinh đó trả lời sai 5 câu.
Trong một cuộc thi có 20 câu hỏi. Mỗi câu trả lời đúng được 10 điểm, mỗi câu trả lời sai bị trừ 3 điểm. Một học sinh đạt được 148 điểm.d) Số câu bạn học sinh đó trả lời đúng là 15 câu.
Một con ếch ở dưới một cái giếng sâu \[10{\rm{ m}}.\] Ban ngày nhảy lên được \[3{\rm{ m}},\] ban đêm tụt xuống \[2{\rm{ m}}.\]
a) Sau mỗi ngày, ếch lên được \[1\,\,{\rm{m}}.\]
Một con ếch ở dưới một cái giếng sâu \[10{\rm{ m}}.\] Ban ngày nhảy lên được \[3{\rm{ m}},\] ban đêm tụt xuống \[2{\rm{ m}}.\]b) Sau 3 ngày, ếch nhảy lên được \[5\,\,{\rm{m}}.\]
Một con ếch ở dưới một cái giếng sâu \[10{\rm{ m}}.\] Ban ngày nhảy lên được \[3{\rm{ m}},\] ban đêm tụt xuống \[2{\rm{ m}}.\]c) Sau 7 ngày, ếch còn cách miệng giếng \[4\,\,{\rm{m}}.\]
Một con ếch ở dưới một cái giếng sâu \[10{\rm{ m}}.\] Ban ngày nhảy lên được \[3{\rm{ m}},\] ban đêm tụt xuống \[2{\rm{ m}}.\]d) Sau 8 ngày thì ếch lên khỏi giếng.
Gọi \[x\] là giá trị thỏa mãn \[{5^{x - 2{\rm{ }}\;}} - {3^{2\;}} = {2^{4\;}} - \left( {{2^8} \cdot {2^{4\;}} - {2^{10}} \cdot {2^2}} \right)\] và \[y\] là giá trị thỏa mãn \[697:\left[ {\left( {15y + 364} \right):y} \right] = 17.\]
a) Giá trị biểu thức \[{2^{4\;}} - \left( {{2^8} \cdot {2^{4\;}} - {2^{10}} \cdot {2^2}} \right)\] bằng 16.
Gọi \[x\] là giá trị thỏa mãn \[{5^{x - 2{\rm{ }}\;}} - {3^{2\;}} = {2^{4\;}} - \left( {{2^8} \cdot {2^{4\;}} - {2^{10}} \cdot {2^2}} \right)\] và \[y\] là giá trị thỏa mãn \[697:\left[ {\left( {15y + 364} \right):y} \right] = 17.\]b) Giá trị \(x = 4\) thỏa mãn biểu thức đã cho.
Gọi \[x\] là giá trị thỏa mãn \[{5^{x - 2{\rm{ }}\;}} - {3^{2\;}} = {2^{4\;}} - \left( {{2^8} \cdot {2^{4\;}} - {2^{10}} \cdot {2^2}} \right)\] và \[y\] là giá trị thỏa mãn \[697:\left[ {\left( {15y + 364} \right):y} \right] = 17.\]
c) Giá trị \(y = 8\) thỏa mãn biểu thức đã cho.
Gọi \[x\] là giá trị thỏa mãn \[{5^{x - 2{\rm{ }}\;}} - {3^{2\;}} = {2^{4\;}} - \left( {{2^8} \cdot {2^{4\;}} - {2^{10}} \cdot {2^2}} \right)\] và \[y\] là giá trị thỏa mãn \[697:\left[ {\left( {15y + 364} \right):y} \right] = 17.\]d) Tích hai giá trị \[x\] và \[y\] cần tìm là 32.
Lúc 6 giờ sáng. Một xe tải và một xe máy cùng xuất phát từ A đến B. Vận tốc xe tải là 50km/h; vận tốc xe máy là 30 km/h. Lúc 8 giờ sáng, một xe con cũng đi từ A đến B với vận tốc 60 km/h. Giả thiết rằng có một xe máy thứ hai cũng xuất phát từ A đến B cùng một lúc với xe tải và xe máy thứ nhất nhưng đi với vận tốc 40 km/h. Hãy viết biểu thức tính quãng đường xe tải, xe máy thứ nhất và xe máy thứ hai đi được sau t giờ.
a) Sau \[t\] giờ, xe tải, xe thứ nhất, xe thứ hai lần lượt đi được quãng đường là \(50t;\,\,30t;\,\,20t.\)
Lúc 6 giờ sáng. Một xe tải và một xe máy cùng xuất phát từ A đến B. Vận tốc xe tải là 50km/h; vận tốc xe máy là 30 km/h. Lúc 8 giờ sáng, một xe con cũng đi từ A đến B với vận tốc 60 km/h. Giả thiết rằng có một xe máy thứ hai cũng xuất phát từ A đến B cùng một lúc với xe tải và xe máy thứ nhất nhưng đi với vận tốc 40 km/h. Hãy viết biểu thức tính quãng đường xe tải, xe máy thứ nhất và xe máy thứ hai đi được sau t giờ.
b) Xe máy thứ hai luôn ở vị trí chính giữa xe tải và xe máy thứ nhất.
Lúc 6 giờ sáng. Một xe tải và một xe máy cùng xuất phát từ A đến B. Vận tốc xe tải là 50km/h; vận tốc xe máy là 30 km/h. Lúc 8 giờ sáng, một xe con cũng đi từ A đến B với vận tốc 60 km/h. Giả thiết rằng có một xe máy thứ hai cũng xuất phát từ A đến B cùng một lúc với xe tải và xe máy thứ nhất nhưng đi với vận tốc 40 km/h. Hãy viết biểu thức tính quãng đường xe tải, xe máy thứ nhất và xe máy thứ hai đi được sau t giờ.c) Quãng đường xe máy thứ hai đi được sau khi xe con xuất phát \[x\] giờ là \(40x\,\,\left( {{\rm{km}}} \right).\)
Lúc 6 giờ sáng. Một xe tải và một xe máy cùng xuất phát từ A đến B. Vận tốc xe tải là 50km/h; vận tốc xe máy là 30 km/h. Lúc 8 giờ sáng, một xe con cũng đi từ A đến B với vận tốc 60 km/h. Giả thiết rằng có một xe máy thứ hai cũng xuất phát từ A đến B cùng một lúc với xe tải và xe máy thứ nhất nhưng đi với vận tốc 40 km/h. Hãy viết biểu thức tính quãng đường xe tải, xe máy thứ nhất và xe máy thứ hai đi được sau t giờ.
d) Xe con ở chính giữa xe máy thứ nhất và xe tải lúc 4 giờ.
Tìm số tự nhiên \(x\) thỏa mãn \[5 \cdot {2^2} + \left( {x + 3} \right) = {5^2}.\]
Tổng \({1^3} + {2^3} + {3^3} + {4^3}\) bằng bình phương của số tự nhiên nào?
Số tự nhiên \(x\) thỏa mãn \({\left( {7x - 25} \right)^3} = {5^2} \cdot {2^5} + 200\) là bao nhiêu?
Có bao nhiêu số tự nhiên \(x\) thỏa mãn \(100 < {5^{2x - 1}} < {5^6}?\)
Biết rằng \({1^2} + {2^2} + {3^2} + \ldots + {10^2} = 385.\) Tính tổng \(S = {2^2} + {4^2} + {6^2} + \ldots + {20^2}.\)






