20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 10. Số nguyên tố (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Số nguyên tố là:
Số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
Số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Số tự nhiên có nhiều hơn một ước.
Số tự nhiên có ba ước.
Số nào dưới đây là số nguyên tố?
7.
4.
9.
10.
Số nào sau đây là hợp số?
13.
31.
100.
37.
Chọn đáp án đúng:
Các số nguyên tố đều là số lẻ.
Số 1 là số nguyên tố.
Số0 là số nguyên tố.
Số 2 là số nguyên tố.
Số 20 có bao nhiêu ước nguyên tố?
1.
2.
3.
6.
Phân tích số 24 ra thừa số nguyên tố ta được:
\(24 = 4 \cdot 2 \cdot 3.\)
\(24 = 8 \cdot 3.\)
\(24 = {2^3} \cdot 3.\)
\(24 = 12 \cdot 2.\)
Chọn khẳng định đúng:
Mọi bội của 3 đều là hợp số.
Mọi số chẵn đều là hợp số.
Tất cả các ước của 3 đều là số nguyên tố.
Số 25 là hợp số.
Có bao nhiêu số nguyên tố có một chữ số?
6.
3.
5.
4.
Hợp số bé nhất là số nào?
4.
0.
2.
1.
Chọn khẳng định sai?
Mọi số tự nhiên đều có ước nguyên tố.
Số 6 có hai ước nguyên tố là 2 và 3.
Một số tự nhiên không phải là số nguyên tố thì là hợp số.
Tổng của hai số nguyên tố có thể là một số chẵn.
Phần II. Trắc nghiệm đúng, sai
Cho \(A = 859 \cdot 37 - 800 \cdot 37;\;{\rm{ }}B = 59 \cdot 12 + 59 \cdot 25.\)
a)\(A\) là hợp số.
b)\(B\) là số nguyên tố.
c)Tổng \(A + B\) là hợp số.
d)Hiệu \(A - B\) là số nguyên tố.
Cho \(A = 555:5 + 324:{18^2}.\)
a)\(A = 114.\)
b)\(A\) là hợp số.
c)\(A\) khi phân tích ra thừa số nguyên tố ta được: \(A = 16 \cdot 7.\)
d)\(A\) có 8 ước.
Cho hai số \(a\) và \(b.\) Biết rằng \(b\) là số nguyên tố và số \(a\) khi phân tích ra thừa số nguyên tố theo sơ đồ cột ta được:
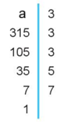
Tích của hai số \(a\) và \(b\)là một số chẵn. Khi đó:
a)\(a = {3^3} \cdot 5 \cdot 7.\)
b)\(a\) có bốn ước nguyên tố.
c)\(b = 2.\)
d)\(a + 4b\) là hợp số.
Cho số \(n = \overline {a2b.} \) Biết rằng \(b\) là số nguyên tố nhỏ nhất và \(a\) hợp số nhỏ nhất.
a)\(b = 3.\)
b)\(a = 4.\)
c)Số \(n\) là số nguyên tố.
d)Phân tích \(n - 2\) ra thừa số nguyên tố ta được \(n - 2 = {2^2} \cdot 3 \cdot 5 \cdot 7.\)
Cho \(a = 24 \cdot 15\) và \(b = 60.\)
a)Phân tích ra thừa số nguyên tố được \(b = 2 \cdot 3 \cdot 10\).
b)Số \(a\) khi phân tích ra thừa số nguyên tố được: \(a = {2^3} \cdot 9 \cdot 5.\)
c)\(a\) có 3 ước nguyên tố.
d)Số ước nguyên tố của \(a\) nhiều hơn số ước nguyên tố của \(b.\)
Phần III. Trắc nghiệm trả lời ngắn
Tìm số tự nhiên \(m\) sao cho \(13 \cdot m\) là số nguyên tố.
Từ ba chữ số \(2;\;{\rm{ }}1;\;{\rm{ }}3\) có thể viết được bao nhiêu số có hai chữ số là số nguyên tố?
Có bao nhiêu số tự nhiên \(a\;\left( {a > 1} \right)\) sao cho \(a - 1;\;{\rm{ }}a;{\rm{ }}\;a + 4\) đều là các số nguyên tố?
Có bao nhiêu chữ số \(a\) để \(\overline {6a} \) là hợp số?
Tìm số nguyên tố \(k\) sao cho \(k + 29\) và \(k + 35\) đều là số nguyên tố.






