20 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 4. Lũy thừa với số mũ tự nhiên (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Số tự nhiên \(n\) thỏa mãn \({4^n} = {4^3} \cdot {4^5}\) là
\(n = 32.\)
\(n = 16.\)
\(n = 8.\)
\(n = 4.\)
\({\left( {{3^2}} \right)^6}\)có kết quả là
\({3^9}.\)
\({3^{12}}.\)
\({3^{18}}.\)
\({3^8}.\)
Viết tích \({9^{12}} \cdot {27^5}\) dưới dạng lũy thừa cơ số 3 là
\({243^{60}}.\)
\({3^{60}}.\)
\({9^{27}}.\)
\({3^{39}}.\)
16 là lũy thừa của số tự nhiên nào và có số mũ bằng bao nhiêu?
Lũy thừa của 2, số mũ bằng 4.
Lũy thừa của 4, số mũ bằng 3.
Lũy thừa của 2, số mũ bằng 3.
Lũy thừa của 8, số mũ bằng 2.
Điền từ thích hợp vào dấu “…”
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và … các số mũ.
nhân.
trừ
cộng.
chia.
Lập phương của 7 được viết là
\({3^7}.\)
\({7^3}.\)
\({7^2}.\)
\({2^7}.\)
Chọn đáp án sai.
\[{5^3}\, < {3^5}.\]
\[{3^4} > {2^5}.\]
\[{4^3}\, = {2^6}.\]
\[{4^3}\, > {8^2}.\]
Tính \({2^4} + 16\) ta được kết quả dưới dạng
\({2^{20}}.\)
\({2^4}.\)
\({2^5}.\)
\({2^{10}}.\)
Giá trị \(x\) thỏa mãn \({x^3} + 15 = 23\) là
\[x = 2.\]
\[x = 3.\]
\[x = 5.\]
\[x = 8.\]
Số tự nhiên \(m\) thỏa mãn \({20^{2025}} < {20^m} < {20^{2027}}\) là
\[m = 2\,024.\]
\(m = 2\,\,027.\)
\(m = 2\,\,026.\)
\(m = 2\,\,025.\)
Cho \(A = {2^{2x + 1}}\) và \(B = {2^{x + 2}}\)\(\left( {x \in \mathbb{N}} \right).\)
(a) Với \(x = 2\) thì \[A + B = 48.\]
(b) Để \(A = 8\) thì \(x = 1.\)
(c) Có 2 giá trị của \(x\) để \(B < 32.\)
(d) Để \(A \cdot B = 64\) thì \(x = 2.\)
Cho \[{a^m}\,\, = \,64\].
(a) \[{a^m}\] là lũy thừa bậc \(m\) của \(a.\)
(b) \[{a^m}:{a^n} = {a^{\frac{{^m}}{n}}}\].
(c) Nếu \(m = 3\) thì \(a = 4\).
(d) Nếu \(a = 8\) thì \(m = 8\).
Cho lũy thừa bậc 3 của \(a\) với \(a \in \mathbb{N}\) và \(a \ne 0.\)
(a) Lũy thừa bậc 3 của \(a\) là tích của \(a\) thừa số bằng nhau, mỗi thừa số bằng 3.
(b) \(a\) được gọi là cơ số.
(c) \({a^3} \cdot {a^4} = {a^7}.\)
(d) \({\left( {{a^3}} \right)^2} = {a^5}.\)
Cho \[a \ne 0,\,\,b \ne 0,\] \[m\,\, = \,5\] và \[n\,\, = \,2\].
(a) \[{a^m}:{a^n}\,\, = \,\,{a^3}.\]
(b) Nếu \[{b^m} = {b^n}\] thì \(b = 2.\)
(c) \[{a^m} \cdot {b^m}\, = \,{\left( {\,a \cdot b} \right)^{10}}.\]
(d) \[{\left( {{a^m}} \right)^n} = {a^{10}}.\]
Tế bào lớn lên đến một kích thước nhất định thì phân chia. Quá trình đó diễn ra như sau: Đầu tiên từ 1 nhân thành 2 nhân tách xa nhau. Sau đó chất tế bào được phân chia, xuất hiện một vách ngăn, ngăn đôi tế bào cũ thành 2 tế bào con. Các tế bào con tiếp tục lớn lên cho đến khi bằng tế bào mẹ. Các tế bào này tiếp tục phân chia thành 4, rồi thành 8, … tế bào.
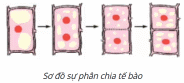
Như vậy từ một tế bào mẹ: sau khi phân chia lần 1 được hai tế bào con; lần hai được \[{2^{2\;}} = 4\] (tế bào con); lần ba được \[{2^3}\; = 8\] (tế bào con). Hãy tính số tế bào con có được ở lần phân chia thứ 5, thứ 8 và thứ 11.
(a) Cứ sau mỗi lần phân chia, số tế bào con nhân đôi so với lần trước đó.
(b) Số tế bào con có được ở lần phân chia thứ 5 là 32 tế bào con.
(c) Số tế bào con có được ở lần phân chia thứ 8 nhiều hơn ở lần thứ 5 là 8 tế bào con.
(d) Để tạo ra 1024 tế bào con thì cần đến lần phân bào thứ 9.
Tìm số tự nhiên \(x\) biết \[25 < {5^{2x - 1}} < {5^5}\].
Tổng các số tự nhiên \(x\) thỏa mãn \({\left( {x - 4} \right)^5} = {\left( {x - 4} \right)^4}\) bằng bao nhiêu?
Số tự nhiên \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = 125\) là bao nhiêu?
Có bao nhiêu số tự nhiên \(x\) thỏa mãn \({5^x} < 90?\)
Trái Đất có khối lượng khoảng \[60 \cdot {10^{20}}\] tấn. Mỗi giây Mặt Trời tiêu thụ \[6 \cdot {10^6}\] tấn khí hydrogen (theo vnexpress.net). Mặt Trời cần bao nhiêu giây để tiêu thụ một lượng khí hydrogen có khối lượng và bằng khối lượng Trái Đất bằng \({10^a}\) tấn. Tính giá trị của \(a.\)


