11 câu hỏi
Trong không gian Oxyz, cho \(\overrightarrow a = \left( {1;2;1} \right)\) và \(\overrightarrow b = \left( { - 1;3;0} \right)\). Vectơ \(\overrightarrow c = 2\overrightarrow a + \overrightarrow b \) có tọa độ là
(1; 7; 2).
(1; 5; 2).
(3; 7; 2).
(1; 7; 3).
Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = \left( {1;2;3} \right),\overrightarrow b = \left( {2;2; - 1} \right),\overrightarrow c = \left( {4;0; - 4} \right)\). Tọa độ của vectơ \(\overrightarrow d = \overrightarrow a - \overrightarrow b + 2\overrightarrow c \) là
(−7; 0; −4).
(−7; 0; 4).
(7; 0; −4).
(7; 0; 4).
Cho \(\overrightarrow a = \left( { - 1; - 1;2} \right),\overrightarrow b = \left( { - 1;1; - 1} \right),\overrightarrow c = \left( {2;4;7} \right)\). Tọa độ của vectơ \(\overrightarrow u = \overrightarrow a - 3\overrightarrow b + 2\overrightarrow c \) là
(0; 10; 13).
(6; −4; 19).
(6; 4; 19).
(−6; 4; 19).
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {3; - 4;1} \right)\) và \(\overrightarrow b = \left( {2; - 1;0} \right)\). Tích vô hướng \(\overrightarrow a .\overrightarrow b \) bằng
11.
10.
9.
8.
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {2;0; - 1} \right),\overrightarrow b = \left( {3; - 5;6} \right)\). Góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng
30°.
120°.
90°.
60°.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(2; 3; −1), N(−1; 1; 1), P(1; m – 1; 2). Tìm m để tam giác MNP vuông tại N.
m = 2.
m = −6.
m = 0.
m = −4.
Trong không gian Oxyz, cho hai điểm A(3; 1; −2), B(2; −3; 5). Điểm M thuộc đoạn AB sao cho MA = 2MB. Tọa độ điểm M là
\(\left( {\frac{7}{3}; - \frac{5}{3};\frac{8}{3}} \right)\).
(4; 5; −9).
\(\left( {\frac{3}{2}; - 5;\frac{{17}}{2}} \right)\).
(1; −7; 12).
Trong không gian Oxyz, cho tam giác ABC có A(1; 0; 1), B(0; 2; 3), C(2; 1; 0). Độ dài đường trung tuyến AM là
\(\frac{1}{2}\).
\(\frac{{\sqrt {11} }}{2}\).
\(\frac{{\sqrt {12} }}{2}\).
\(\frac{{\sqrt {10} }}{2}\).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\overrightarrow {OM} = \left( {1;5;2} \right)\], \[\overrightarrow {ON} = \left( {3;7; - 4} \right)\], \(K\left( { - 1;3;1} \right)\). Gọi \[P\] là điểm đối xứng với \[M\] qua \[N\]. Tìm tọa độ vectơ \[\overrightarrow {KP} \].
\(\overrightarrow {KP} = \left( {6;6; - 11} \right)\).
\[\overrightarrow {KP} = \left( {8;6; - 11} \right)\].
\[\overrightarrow {KP} = \left( {6;6; - 4} \right)\].
\[\overrightarrow {KP} = \left( {3;3; - 2} \right)\].
Trong không gian \[Oxyz\] cho tam giác \[ABC\] có \[A\left( {1; - 1;1} \right),\,B\left( {5;0;2} \right),\,C\left( {0;4;3} \right)\]. Toạ độ trọng tâm \(G\)của tam giác \[ABC\] là
\(G\left( {3;\frac{5}{2};3} \right)\).
\(G\left( {2; - 1;2} \right)\).
\(G\left( {3; - \frac{5}{2};3} \right)\).
\(G\left( {2;1;2} \right)\).
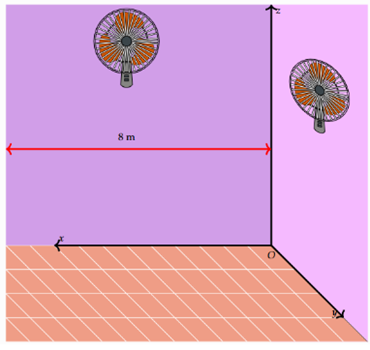
Trong một căn phòng dạng hình hộp chữ nhật với chiều dài 8m, rộng 6m và cao 4m có 1 cây quạt treo tường. Cây quạt A treo chính giữa bức tường và cách trần 1m, cây quạt B treo chính giữa bức tường và cách trần 1,5m. Chọn hệ trục tọa độ Oxyz như hình vẽ bên dưới (đơn vị mét). Giả sử \(\overrightarrow {AB} = \left( {a;b;c} \right)\). Tính a + b + c.