20 câu Trắc nghiệm Toán 12 Cánh diều Bài 3. Đường tiệm cận của đồ thị hàm số có đáp án
20 câu hỏi
I. Nhận biết
Cho hàm số y = f(x) có đồ thị như hình vẽ
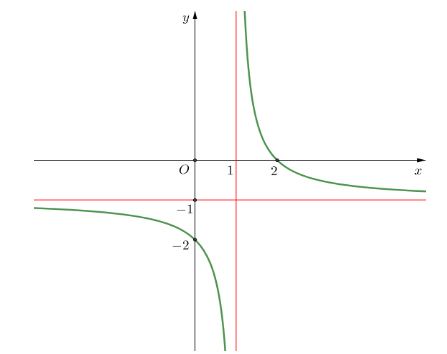
Đồ thị hàm số đã cho có tiệm cận đứng bằng
x = 1.
x = −1.
x = 0.
y = −1.
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\). Khẳng định nào sau đây đúng?
Đồ thị hàm số có hai đường tiệm cận.
Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ 2 \right\}\).
Hàm số có một cực trị.
Giao điểm của đồ thị và trục tung là \(\left( { - 1\,;\,0} \right)\)
Cho hàm số \(y = \frac{{2x + 1}}{{x - 2}}\). Khẳng định nào dưới đây là đúng?
Hàm số có cực trị.
Đồ thị hàm số có tiệm cận đứng là \(x = 2\).
Đồ thị hàm số đi qua điểm \(A\left( {1;3} \right)\).
Hàm số nghịch biến trên \(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right)\).
Cho hàm số y = f(x) có đồ thị như hình vẽ
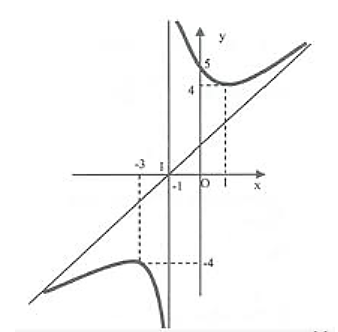
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
4.
2.
1.
3.
Đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 3}}\) có một đường tiệm cận ngang là
\(x = 3\).
\(y = 2\).
\(x = - 3\).
\(y = - 2\).
II. Thông hiểu
Đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 3}}\) có bao nhiêu đường tiệm cận?
\(0.\)
\(1.\)
\(2.\)
\(3.\)
Viết phương trình các đường tiệm cận của đồ thị hàm số \(y = \frac{{x + 3}}{{2 - x}}\) ?
\(x = 2\) và \(y = - 1\).
\(x = - 1\) và \(y = 2\).
\(x = 2\) và \(y = \frac{1}{2}\).
\(x = - 1\) và \(y = \frac{1}{2}\).
Đường thẳng y = −1 là tiệm cận của đồ thị hàm số nào dưới đây?
\(y = \frac{{x + 3}}{{2 - x}}\).
\(y = \frac{1}{{x + 1}}\) .
\(y = \frac{{ - 2x + 1}}{{2 + x}}\) .
\(y = \frac{{ - {x^2} + 3}}{{x - 1}}\) .
Đường thẳng \(x = - 1\) không là tiệm cận của đồ thị hàm số nào dưới đây?
\(y = \frac{{x + 2}}{{\left| x \right| - 1}}.\)
\(y = \frac{1}{{{x^3} + 1}}.\)
\(y = \frac{{ - {x^2} + x + 2}}{{x + 1}}.\)
\(y = \frac{2}{{{x^2} + 3x + 2}}.\)
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) có bảng biến thiên như hình bên.
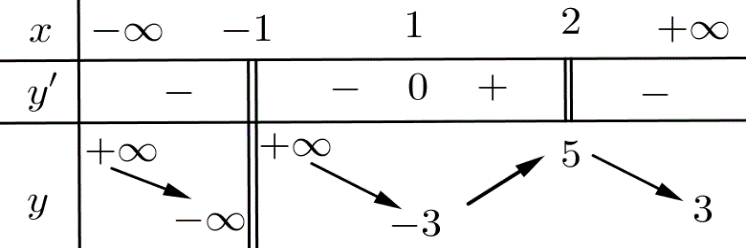
Số tiệm cận của đồ thị hàm số đã cho là.
\(1.\)
\(2.\)
\(3.\)
\(4.\)
Cho hàm số y = f(x) có bảng biến thiên như sau:
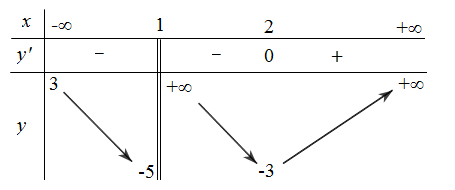
Số các đường tiệm cận (tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số đã cho bằng
\(3\).
\(2\).
\(4\).
\(1\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
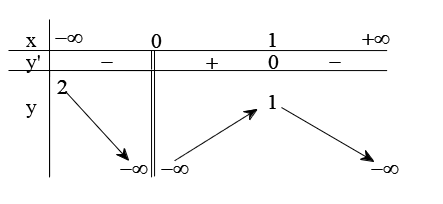
Tổng số đường tiệm cận của đồ thị hàm số \[y = f\left( x \right)\]là
\[1\].
\[0\].
\[3\].
\[2\].
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây. Phương trình đường tiệm cận xiên của đồ thị hàm số là
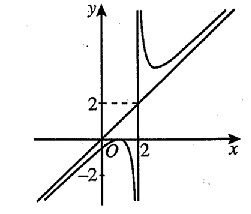
y = x.
y = −x.
y = x + 2.
y = 2x.
Đường tiệm cận xiên của đồ thị hàm số \(y = 2x - 1 + \frac{3}{{x + 1}}\) là
y = 2x.
y = x + 1.
y = 2x − 1.
y = 1 − 2x.
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x + 3}}{{x + 1}}\) là
y = x.
y = x + 1.
y = x − 1.
y = 1 − 2x.
III. Vận dụng
Đồ thị hàm số nào dưới đây có đường tiệm cận ngang qua điểm \(A\left( {2;3} \right)\)
\(y = \frac{{x + 3}}{{3x + 2}}\).
\(y = \frac{{2x + 1}}{{x - 2}}\).
\(y = \frac{{3x + 1}}{{2x - 2}}\).
\(y = \frac{{3x + 2}}{{x + 3}}\).
Tìm tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số \[y = \frac{{3 - x}}{{2x + 5}}\]
\(\left( { - \frac{1}{2};\, - \frac{5}{2}} \right).\)
\(\left( { - \frac{5}{2};\,\frac{3}{2}} \right).\)
\(\left( { - \frac{5}{2};\, - \frac{1}{2}} \right).\)
\(\left( { - \frac{1}{2};\,\frac{5}{2}} \right).\)
Cho hàm số y = f(x) có bảng biến thiên
![Cho hàm số y = f(x) có bảng biến thiên Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để đồ thị hàm số có 4 tiệm cận. (ảnh 1)](https://video.vietjack.com/upload2/images/1728876922/1728877622-image6.png)
Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để đồ thị hàm số có 4 tiệm cận.
5.
6.
7.
8.
Tiệm cận đứng của đồ thị hàm số \(y = \frac{x}{{{x^2} - 4x}}\) là
\(x = 0.\)
\(x = - 4.\)
\(x = 0\); \(x = 4.\)
\(x = 4.\)
Cho đồ thị hàm số y = f(x) có bảng biến thiên xác định như hình. Biết rằng đồ thị hàm số có tiệm cận đứng x = x0, tiệm cận ngang y = y0 và x0y0 = 16. Tìm m.
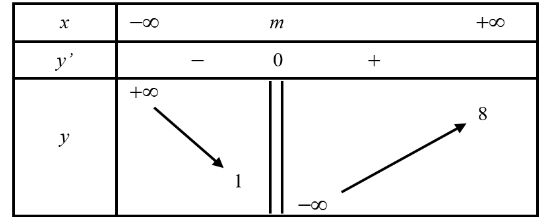
m = 8.
m = −16.
m = 1.
m = 2.