20 câu Trắc nghiệm Toán 12 Cánh diều Bài 1. Vectơ và các phép toán vectơ trong không gian có đáp án
20 câu hỏi
I. Nhận biết
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\).
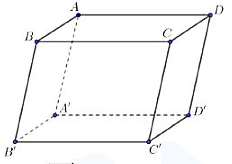
Vectơ nào sau đây cùng phương với \(\overrightarrow {BC} \) ?
\(\overrightarrow {DC} .\)
\(\overrightarrow {DA} .\)
\(\overrightarrow {BB'} .\)
\(\overrightarrow {C'C} .\)
Cho hình chóp \(S.ABC\). Tổng của hai vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {AB} \) là
\(\overrightarrow {BS} .\)
\(\overrightarrow {BA} .\)
\(\overrightarrow {SB} .\)
\(\overrightarrow {SC} .\)
Cho khối lập phương \(ABCD.A'B'C'D'\). Khi đó, góc giữa vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {AD} \) là
\(90^\circ.\)
\(60^\circ.\)
\(45^\circ.\)
\(30^\circ.\)
Cho hình lập phương \(ABCD.A'B'C'D'\). Khẳng định nào sau đây là sai?
\(\left( {\overrightarrow {AB} ,\overrightarrow {A'D'} } \right) = 90^\circ.\)
\(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right) = 45^\circ.\)
\(\left( {\overrightarrow {AC} ,\overrightarrow {B'D'} } \right) = 90^\circ.\)
\(\left( {\overrightarrow {A'A} ,\overrightarrow {CB'} } \right) = 45^\circ.\)
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
\(\overrightarrow a.\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right).\)
\(\overrightarrow a.\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right).\)
\(\overrightarrow a.\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right).\)
\(\overrightarrow a.\overrightarrow b = 0.\)
II. Thông hiểu
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M\) là trung điểm của cạnh \(BB'\). Đặt \(\overrightarrow {CA} = \overrightarrow a \), \(\overrightarrow {CB} = \overrightarrow b \), \(\overrightarrow {AA'} = \overrightarrow c \). Khẳng định nào sau đây đúng?
\(\overrightarrow {AM} = \overrightarrow a + \overrightarrow c - \frac{1}{2}\overrightarrow b.\)
\(\overrightarrow {AM} = \overrightarrow b + \overrightarrow c - \frac{1}{2}\overrightarrow a.\)
\(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c.\)
\(\overrightarrow {AM} = \overrightarrow a - \overrightarrow c + \frac{1}{2}\overrightarrow b.\)
Cho tứ diện \(ABCD\). Lấy \(G\) là trọng tâm tam giác \(BCD\). Phát biểu nào sau đây là sai?
\(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 .\)
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 .\)
\(\overrightarrow {CB} + \overrightarrow {CD} = 3\overrightarrow {CG} .\)
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} .\)
Cho hình lăng trụ \(ABC.A'B'C'\). Chọn khẳng định đúng trong các khẳng định dưới đây:
\(\overrightarrow {B'C} = \overrightarrow {AA'} + \overrightarrow {AB} - \overrightarrow {AC} .\)
\(\overrightarrow {B'C} = - \overrightarrow {AA'} + \overrightarrow {AB} - \overrightarrow {AC} .\)
\(\overrightarrow {B'C} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AC} .\)
\(\overrightarrow {B'C} = - \overrightarrow {AA'} - \overrightarrow {AB} + \overrightarrow {AC} .\)
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
\(\overrightarrow a.\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\)
\(\overrightarrow a.\overrightarrow b = 0.\)
\(\overrightarrow a.\overrightarrow b = - 1.\)
\(\overrightarrow a.\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\)
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) thỏa mãn: \(\left| {\overrightarrow a } \right| = 4\); \(\left| {\overrightarrow b } \right| = 3\); \(\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi \(\alpha \) là góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b \). Chọn khẳng định đúng ?
\(\cos \alpha = \frac{3}{8}.\)
\(\alpha = 30^\circ.\)
\(\cos \alpha = \frac{1}{3}.\)
\(\alpha = 60^\circ.\)
Cho hình lập phương \(ABCD.EFGH\) có cạnh bằng \(a\). Ta có: \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng:
\({a^2}\sqrt 2 .\)
\({a^2}.\)
\({a^2}\sqrt 3 .\)
\(\frac{{{a^2}\sqrt 2 }}{2}.\)
Cho hình lăng trụ \(ABC.A'B'C'\) đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c .\) Gọi \(G'\) là trọng tâm của tam giác \(A'B'C'\). Vectơ \(\overrightarrow {AG'} \) bằng
\(\overrightarrow {AG'} = \frac{1}{3}\left( {\overrightarrow a + 3\overrightarrow b + \overrightarrow c } \right).\)
\(\overrightarrow {AG'} = \frac{1}{3}\left( {3\overrightarrow a + \overrightarrow b + \overrightarrow c } \right).\)
\(\overrightarrow {AG'} = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + 3\overrightarrow c } \right).\)
\(\overrightarrow {AG'} = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right).\)
Cho hình chóp đều \(S.ABCD\) có tất cả các cạnh bằng \(2\sqrt 3 \). Tính độ dài vectơ \(\overrightarrow u = \overrightarrow {SA} - \overrightarrow {SC} .\)
\(\sqrt 3 .\)
\(\sqrt 2 .\)
\(2\sqrt 6 .\)
\(2\sqrt 2 .\)
Cho hình chóp \(S.ABC\) có \(AB = 4\), \(\widehat {BAC} = 60^\circ \), \(\overrightarrow {AB} .\overrightarrow {AC} = 6\). Khi đó độ dài \(\overrightarrow {AC} \) là
\(3.\)
\(6.\)
\(4.\)
\(12.\)
Trong không gian, cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Trong các mệnh đề dưới đây, có bao nhiêu mệnh đề sai?
a) \(\overrightarrow {B'B} - \overrightarrow {DB} = \overrightarrow {B'D} .\)
b) \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD} .\)
c) \(\left| {\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} } \right| = a\sqrt 2 .\)
d) \(\left| {\overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} } \right| = a.\)
\(2.\)
\(3.\)
\(1.\)
\(4.\)
III. Vận dụng
Một chiếc đèn chùm treo có khối lượng \(m = 5\) kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích \(SA,SB,SC,SD\) sao cho \(S.ABCD\) là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \). Biết \(\overrightarrow P = m.\overrightarrow g \) trong đó \(\overrightarrow g \) là vectơ gia tốc rơi tự do có độ lớn \(10\)m/s2, \(\overrightarrow P \) là trọng lượng của vật có đơn vị kg.
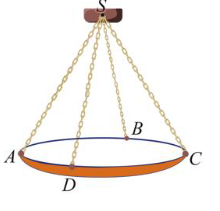
Khi đó:
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vectơ đồng phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|.\)
c) Độ lớn của trọng lực \(\overrightarrow P \) tác động lên chiếc đèn chùm bằng \(50N\).
d) Độ lớn của lực căng cho mỗi sợi xích bằng \(\frac{{25\sqrt 3 }}{2}N\).
Số mệnh đề đúng trong các mệnh đề trên là:
\(1.\)
\(2.\)
\(3.\)
\(4.\)
Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat {BAC} = \widehat {BAD} = 60^\circ \), \(\widehat {CAD} = 90^\circ \). Gọi \(I\) và \(J\) lần lượt là trung điểm của \(AB\) và \(CD\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \) ?
\(120^\circ.\)
\(90^\circ.\)
\(60^\circ.\)
\(30^\circ.\)
Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(M\) là trung điểm của \(BC\).
Tính \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right)\).
\(\frac{{\sqrt 3 }}{6}.\)
\(\frac{{\sqrt 6 }}{3}.\)
\(\frac{{\sqrt 3 }}{2}.\)
\(\frac{{\sqrt 3 }}{2}.\)
Cho hình chóp \(S.ABC\) có \(SA = SB = SC\) và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {BC} \) ?
\(120^\circ.\)
\(90^\circ.\)
\(60^\circ.\)
\(45^\circ.\)
Cho tứ diện \(ABCD\). Gọi \(E,F\) là các điểm lần lượt thuộc các cạnh \(AB,CD\) sao cho \(AE = \frac{1}{3}AB,CF = \frac{1}{3}CD\). Tìm giá trị \(k\) với \(k \in \mathbb{R}\) thỏa mãn đẳng thức:
\(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AD} + k.\overrightarrow {BC} + \frac{1}{3}.\overrightarrow {AB} \).
\(k = \frac{2}{3}.\)
\(k = \frac{1}{3}.\)
\(k = \frac{3}{4}.\)
\(k = \frac{4}{3}.\)