10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh a, cạnh bên SA vuông góc với mặt phẳng (ABCD) và SD = 2a. Tính khoảng cách từ S đến mặt phẳng (ABCD).
\(a\sqrt 5 \).
\(\frac{a}{2}\).
3a.
\(a\sqrt 3 \).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ^ (ABC). Gọi H và K lần lượt là hình chiếu của A lên SB và SC. Mệnh đề nào sau đây sai?
d(S, (ABC)) = SA.
d(C, (SAB)) = BC.
d(A, (SBC)) = AH.
d(A, (SBC)) = AK.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA ^ (ABCD). Gọi I là trung điểm của SC. Khoảng cách từ I đến mặt phẳng (ABCD) bằng độ dài đoạn thẳng nào?
IB.
IC.
IA.
IO.
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a (tham khảo hình vẽ).
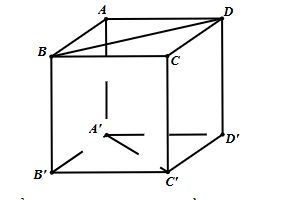
Khoảng cách giữa hai đường thẳng BD và A'C' bằng
a.
\(\sqrt 2 a\).
\(\frac{{\sqrt 3 }}{2}a\).
\(a\sqrt 3 \).
Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {BCD} \right)\) bằng:
\(\frac{{a\sqrt 3 }}{4}\).
\(\frac{{a\sqrt 3 }}{3}\).
\(\frac{{a\sqrt 6 }}{3}\).
\(\frac{{a\sqrt 6 }}{2}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\). Tính khoảng cách \(d\) giữa hai đường thẳng \(SB\) và \(CD\).
\(d = 2a\).
\(d = a\sqrt 3 \).
\(d = a\sqrt 2 \).
\(d = a\).
Cho lăng trụ tam giác đều \[ABC.A'B'C'\] có \[AB = a\], \[AA' = 2a\]. Khoảng cách giữa \(AB'\) và \[CC'\] bằng
\(\frac{{2a\sqrt 5 }}{5}\).
\(a\).
\(a\sqrt 3 \).
\(\frac{{a\sqrt 3 }}{2}\).
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính khoảng cách giữa hai đường thẳng BB', AD.
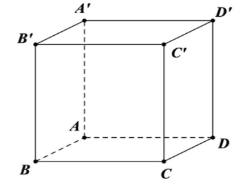
\(\frac{{a\sqrt 2 }}{2}\).
\(a\sqrt 2 \).
a.
\(\frac{{a\sqrt 3 }}{3}\).
Hình chóp S.ABC có SA ^ (ABC), tam giác ABC vuông tại A với AB = a; \(AC = a\sqrt 3 \). Khoảng cách giữa hai đường thẳng SA, BC bằng
\(\frac{{a\sqrt 2 }}{3}\).
\(\frac{{a\sqrt 2 }}{2}\).
\(\frac{{a\sqrt 3 }}{2}\).
\(\frac{{a\sqrt 3 }}{3}\).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng
a.
\(\frac{{a\sqrt 5 }}{2}\).
\(\frac{{a\sqrt 3 }}{2}\).
\(a\sqrt 2 \).
