10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Với ba tia Ou, Ov, Ow bất kì. Công thức nào sau đây là đúng:
(Ou, Ov) + (Ow, Ov) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
(Ou, Ov) + (Ov, Ow) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
(Ou, Ov) − (Ov, Ow) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
(Ou, Ov) − (Ow, Ov) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
Công thức nào sau đây là đúng về mối quan hệ giữa góc và rad ?
\[1^\circ = \frac{\pi }{{360}}\] rad.
\[1^\circ = \frac{\pi }{{180}}\] rad.
\[1\,\,rad\,{\rm{ = }} - {\left( {\frac{{{\rm{90}}}}{{\rm{\pi }}}} \right)^o}\].
\[1\,\,rad\,{\rm{ = }}{\left( {\frac{{{\rm{90}}}}{{\rm{\pi }}}} \right)^o}\].
Cho một góc lượng giác (Ox, Ou) có số đo−30° và một góc lượng giác (Ox, Ov) có số đo 120°. Tính số đo góc lượng giác (Ou, Ov).
\[150^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
\[ - 150^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
\[90^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
\[ - 90^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
Cho \[\widehat {{\rm{uOv}}}{\rm{ = 36}}^\circ \].Giá trị \[\widehat {{\rm{uOv}}}\]khi đổi sang rad là:
\[\frac{\pi }{4}\].
\[\frac{\pi }{5}\].
\[\frac{{3\pi }}{4}\].
\[\frac{{2\pi }}{5}\].
Cho \[\widehat {{\rm{uOv}}}{\rm{ = }}\frac{{{\rm{5\pi }}}}{{\rm{6}}}\]. Giá trị \[\widehat {{\rm{uOv}}}\] khi đổi sang độ là:
30°.
120°.
150°.
60°.
Trên đường tròn lượng giác, cho góc lượng giác có số đo \[\frac{\pi }{3}\] rad thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác trên đều có số đo dạng:
\(\frac{\pi }{3}\).
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k}}\frac{{\rm{\pi }}}{{\rm{2}}}{\rm{,(k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
Góc lượng giác (Ox, Ot) có một số đo là \[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + 2023\pi , (k}} \in \mathbb{Z}{\rm{)}}\], số đo tổng quát của góc lượng giác (Ox, Ot) là:
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
Trên hình vẽ hai điểm \[M,N\] biểu diễn các cung có số đo là:
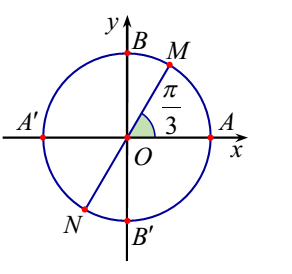
\[x = \frac{\pi }{3} + 2k\pi \].
\[x = - \frac{\pi }{3} + k\pi \].
\[x = \frac{\pi }{3} + k\pi \].
\[x = \frac{\pi }{3} + k\frac{\pi }{2}.\]
Hình vẽ bên là vòng tròn lượng giác gốc A, trong đó M1M2M3M4 là hình vuông, \(\widehat {AO{M_1}} = 45^\circ \). Các điểm nào sau đây biểu diễn đẩy đủ các góc lượng giác \( - \frac{\pi }{2} + k2\pi \).
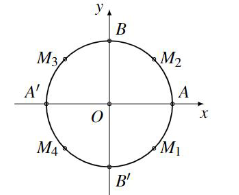
Điểm B'.
Điểm B, B'.
Điểm M4.
Điểm M4, M5.
Hình vẽ bên là vòng tròn lượng giác gốc A, trong đó M1M2M3M4 là hình vuông, \(\widehat {AO{M_1}} = 45^\circ \). Điểm A biểu diễn đầy đủ các góc lượng giác có số đo là: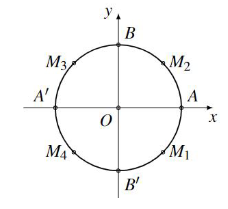
\[x = \frac{\pi }{4} + 2k\pi \].
\[x = \frac{{2\pi }}{3} + k\pi \].
\[k2\pi \].
\[k\pi .\]
