19 câu hỏi
Phát biểu nào sau đây là đúng ?
Cho hai tia Ou, Ov thì có duy nhất góc lượng giác tia đầu Ou, tia cuối Ov.
Số đo góc lượng giác luôn dương.
sđ (Ov,Ou) = sđ (Ou,Ov).
Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo của nó.
Cho góc hình học \[\widehat {{\rm{uOv}}}{\rm{ = 4}}{{\rm{5}}^{\rm{0}}}\]. Xác định số đo của góc lượng giác (Ou,Ov) trong hình dưới đây:
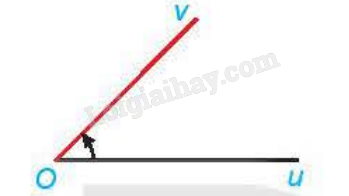
\[{\rm{4}}{{\rm{5}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
\[{\rm{ - 4}}{{\rm{5}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
\[{\rm{13}}{{\rm{5}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
\[{\rm{ - 13}}{{\rm{5}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
Với ba tia Ou, Ov, Ow bất kì.Công thức nào sau đây là đúng:
sđ (Ou,Ov) + sđ (Ow,Ov) = sđ (Ou,Ow) + \[k{360^0}(k \in Z)\]
sđ (Ou,Ov) + sđ (Ov,Ow) = sđ (Ou,Ow) + \[k{360^0}(k \in Z)\]
sđ (Ou,Ov) − sđ (Ov,Ow) = sđ (Ou,Ow) + \[k{360^0}(k \in Z)\]
sđ (Ou,Ov) − sđ (Ow,Ov) = sđ (Ou,Ow) + \[k{360^0}(k \in Z)\]
Công thức nào sau đây là đúng về mối quan hệ giữa góc và rad ?
\[{{\rm{1}}^{\rm{0}}}{\rm{ = }}\frac{{\rm{\pi }}}{{{\rm{360}}}}\] rad
\[{{\rm{1}}^{\rm{0}}}{\rm{ = }}\frac{{\rm{\pi }}}{{{\rm{180}}}}\] rad
\[1\,\,rad\,{\rm{ = }} - {\left( {\frac{{{\rm{90}}}}{{\rm{\pi }}}} \right)^{\rm{0}}}\]
\[1\,\,rad\,{\rm{ = }}{\left( {\frac{{{\rm{90}}}}{{\rm{\pi }}}} \right)^{\rm{0}}}\]
Cho một góc lượng giác (Ox, Ou) có số đo −300 và một góc lượng giác (Ox, Ov) có số đo 1200. Tính số đo góc lượng giác (Ou, Ov).
\[{\rm{15}}{{\rm{0}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
\[ - {\rm{15}}{{\rm{0}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
\[{\rm{9}}{{\rm{0}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
\[ - {\rm{9}}{{\rm{0}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]
Cho \[\widehat {{\rm{uOv}}}{\rm{ = 3}}{{\rm{6}}^{\rm{0}}}\].Giá trị \[\widehat {{\rm{uOv}}}\]khi đổi sang rad là:
\[\frac{\pi }{4}\]
\[\frac{\pi }{5}\]
\[\frac{{3\pi }}{4}\]
\[\frac{{2\pi }}{5}\]
Cho \[\widehat {{\rm{uOv}}}{\rm{ = }}\frac{{{\rm{5\pi }}}}{{\rm{6}}}\]. Giá trị \[\widehat {{\rm{uOv}}}\] khi đổi sang độ là:
300
1200
1500
600
Một đường tròn có đường kính là 50cm. Độ dài của cung trên đường tròn có số đo 1200 là:
104,72cm
26,18cm
78,54cm
52,36cm
Trên đường tròn lượng giác, cho góc lượng giác có số đo \[\frac{\pi }{3}\] rad thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác trên đều có số đo dạng:
\(\frac{\pi }{3}\)
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k}}\frac{{\rm{\pi }}}{{\rm{2}}}{\rm{,(k}} \in {\rm{Z)}}\]
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in {\rm{Z)}}\]
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in {\rm{Z)}}\]
Góc lượng giác (Ox, Ot) có một số đo là \[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + 2023\pi , (k}} \in {\rm{Z)}}\], số đo tổng quát của góc lượng giác (Ox, Ot) là:
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in {\rm{Z)}}\]
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in {\rm{Z)}}\]
\[\frac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in {\rm{Z)}}\]
\[\frac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in {\rm{Z)}}\]
Cho \[\left( {Ou,Ov} \right) = {\rm{3}}{{\rm{5}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\]Với giá trị nào của k thì (Ou,Ov) = 7550?
k = 1
k = −2
k = 2
k = 3
Cho \[\left( {Ou,Ov} \right){\rm{ = }} - {\rm{1}}{{\rm{2}}^{\rm{0}}}{\rm{ + k36}}{{\rm{0}}^{\rm{0}}}{\rm{(k}} \in {\rm{Z)}}\] . Với giá trị nào của k thì \[\left( {{\rm{Ou, Ov}}} \right){\rm{ = }}\frac{{{\rm{59\pi }}}}{{{\rm{15}}}}\]
k = 2
k = −2
k = −3
k = 3
Cho \[\;\left( {{\rm{Ou,Ov}}} \right){\rm{ = }}\frac{{{\rm{2023\pi }}}}{{\rm{3}}}\] thì số đo góc hình học \[\widehat {{\rm{uOv}}}\]bằng?
\[\frac{{{\rm{2\pi }}}}{{\rm{3}}}\]
\[\frac{{\rm{\pi }}}{{\rm{3}}}\]
\[\frac{{{\rm{5\pi }}}}{{\rm{3}}}\]
\[\frac{{{\rm{8\pi }}}}{{\rm{3}}}\]
Một đồng hồ treo tường, kim giờ dài 11cm. Trong 40 phút mũi kim giờ vạch lên cung tròn có độ dài là:
3,8cm
3,82cm
3,84cm
3,86cm
Bánh xe đạp có bán kính 50cm. Một người quay bánh xe 5 vòng quanh trục thì quãng đường đi được là:
\[{\rm{250\pi (cm)}}\]
\[{\rm{1000\pi (cm)}}\]
\[{\rm{500\pi (cm)}}\]
\[{\rm{200\pi (cm)}}\]
Hai góc lượng giác \(\frac{\pi }{3}\) và \[\frac{{{\rm{m\pi }}}}{{{\rm{12}}}}\] có cùng tia đầu và tia cuối khi m có giá trị là:
m = 4 + 24k
m = 4 + 14k
m = 4 + 20k
m = 4 + 22k
Góc lượng giác (Ou, Ov) có số là \[ - \frac{{{\rm{133\pi }}}}{{\rm{3}}}\]thì góc (Ou, Ov) có số đo dương nhỏ nhất là:
\[\frac{{{\rm{10\pi }}}}{{\rm{3}}}\]
\[\frac{{{\rm{11\pi }}}}{{\rm{3}}}\]
\[\frac{{{\rm{8\pi }}}}{{\rm{3}}}\]
\[\frac{{{\rm{5\pi }}}}{{\rm{3}}}\]
Cho hai góc lượng giác có sđ(Ox, Ou) = \[{\rm{4}}{{\rm{5}}^{\rm{0}}}{\rm{ + m36}}{{\rm{0}}^{\rm{0}}}{\rm{(m}} \in {\rm{Z)}}\] và sđ(Ox, Ov) = \[ - {\rm{13}}{{\rm{5}}^{\rm{0}}}{\rm{ + n36}}{{\rm{0}}^{\rm{0}}}{\rm{(n}} \in {\rm{Z)}}\]. Ta có hai tia Ou và Ov:
Tạo với nhau góc 450
Trùng nhau
Đối nhau
Vuông góc
Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay được góc 2700 ?
\(\frac{2}{3}\) phút
\(\frac{1}{3}\) phút
\(\frac{1}{4}\) phút
\(\frac{1}{2}\) phút
